Công Thức Đạo Hàm Log, Căn Bậc 3 , Căn U, Căn X, Căn Logarit
Có thể bạn quan tâm
Tiếp tục ở chuyên mục Toán Học hôm nay, THPT Chuyên Lam Sơn xin gửi đến các bạn bảng công thức đạo hàm trong toán học đầy đủ và chi tiết với các công thức đạo hàm căn như: Đạo hàm căn bậc 3 , đạo hàm căn bậc 3 của x , đạo hàm căn bậc 3 của x² , đạo hàm căn u , đạo hàm bậc 2 , đạo hàm căn bậc 2 của x , căn u đạo hàm , công thức đạo hàm log , công thức đạo hàm logarit , đạo hàm căn x ….giúp các bạn có thể áp dụng vào làm bài tập.
Nội Dung
- Định nghĩa đạo hàm
- Quy tắc cơ bản của đạo hàm
- Công thức đạo hàm từ cơ bản đến nâng cao
- 1. Công thức đạo hàm cơ bản
- 2. Công thức đạo hàm lượng giác3. Bảng đạo hàm
- Các dạng bài tập liên quan đến công thức đạo hàm
- Dạng 1: Tính đạo hàm bằng định nghĩa
- Dạng 2: Tính đạo hàm bằng công thức
- Dạng 3: Tính đạo hàm của hàm số lượng giác
- Dạng 4: Chứng minh đẳng thức, giải phương trình, bất phương trình liên quan đến đạo hàm
Định nghĩa đạo hàm
Giới hạn, nếu có, của tỉ số giữa số gia của hàm số và số gia của đối số tại x0, khi số gia của đối số tiến dần tới 0, được gọi là đạo hàm của hàm số y = f(x) tại điểm x0
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b):
![]()
Nếu hàm số y = f(x) có đạo hàm tại x0 thì nó liên tục tại điểm đó.
Quy tắc cơ bản của đạo hàm

Quy tắc đạo hàm của hàm số hợp
Nếu y = y(u(x)) thì y'(x) = y'(u) . u'(x)
Công thức đạo hàm từ cơ bản đến nâng cao
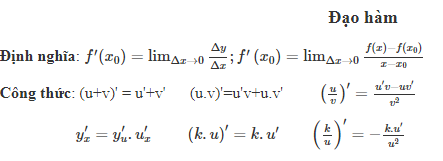

1. Công thức đạo hàm cơ bản

2. Công thức đạo hàm lượng giác 3. Bảng đạo hàm
3. Bảng đạo hàm

Xem thêm:
- Công thức lượng giác
- Công thức logarit
- Tích vô hướng
- Bảng nguyên hàm
- Hệ thức lượng giác trong tam giác
Các dạng bài tập liên quan đến công thức đạo hàm
Dạng 1: Tính đạo hàm bằng định nghĩa
Phương pháp:
Bước 1. Giả sử Δx là số gia của đối số x tại x0, tính Δy = f(x0 + Δx) – f(x0).
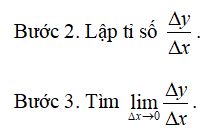
Lưu ý: Trong định nghĩa trên đây, thay xo bởi x ta sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số y = f(x) tại điểm x ∈ (a, b)
Ví dụ 1: Cho hàm số f(x) = 3x + 5.Tính đạo hàm của hàm số đã cho bằng định nghĩa.
Lời giải:
Tập xác định của hàm số đã cho là D = R
Ta có Δy = 3(x+Δx) + 5 – 3x – 5 = 3Δx
Khi đó:
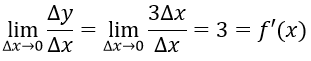
Ví dụ 2: Cho hàm số 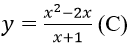
Đạo hàm của hàm số đã cho tại x = 1?
Lời giải
với Δx là số gia của đối số tại x = 1, ta có
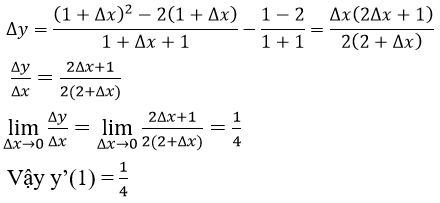
Dạng 2: Tính đạo hàm bằng công thức
Phương pháp: Sử dụng các công thức đạo hàm để áp dụng vào làm bài tập
Ví dụ 1: Đạo hàm của hàm số y = 5x + 3x(x + 1) – 5 tại x = 0 bằng bao nhiêu?
Lời giải
Ta có: y = 3x2 + 8x – 5 ⇒ y’ = 6x + 8
Vậy y’(0) = 8
Ví dụ 2: Đạo hàm của hàm số y = 3x5 – 2x4 tại x = -1, bằng bao nhiêu?
Lời giải
y’ = 15x4 – 8x3 ⇒ y’(-1) = 15 + 8 = 23
Ví dụ 3: Đạo hàm của hàm số y = (2x4 – 3x2 – 5x)(x2 – 7x) bằng bao nhiêu?
Lời giải
Áp dụng công thưc đạo hàm hàm hơp (uv)’= u’v + uv’ ta có:
y’ = (8x3 – 6x – 5)(x2 – 7x) + (2x4 – 3x2 – 5x)(2x – 7)
Ví dụ 4: Đạo hàm của hàm số ![]()
Lời giải
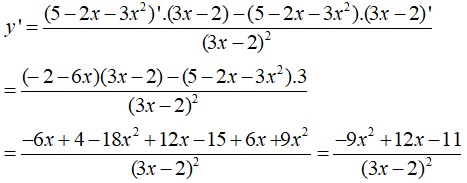
Dạng 3: Tính đạo hàm của hàm số lượng giác
Phương pháp giải:
- Áp dụng các công thức đạo hàm của các hàm số lượng giác.
- Áp dụng quy tắc đạo hàm của tổng, hiệu, tích, thương và hàm số hợp.
Ví dụ 1: Tính đạo hàm của hàm số y = cosx + cos4x + sin5x
Lời giải
Ta có: y’ = -2sin2x – 4sin4x + 5cos5x
Ví dụ 2: Tính đạo hàm của hàm số y = tan(2x+1) – xcos2x
Lời giải
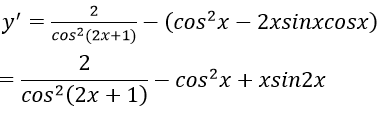
Ví dụ 3: Tính đạo hàm của hàm số y = 6(sin4x + cos4x) – 4(sin6x + cos6x)
Lời giải
y’ = 6(sin2x + cos2x)2 – 12sin2xcos2x – 4(sin2x + cos2x)2 + 12sin2xcos2x(sin2x + cos2x) = 2
Dạng 4: Chứng minh đẳng thức, giải phương trình, bất phương trình liên quan đến đạo hàm
Ví dụ 1: Chứng minh rằng:
a) Hàm số y = tan x thoả mãn hệ thức y’ – y2 – 1 = 0.
b) Hàm số y = cot 2x thoả mãn hệ thức y’ + 2y2 + 2 = 0.
Lời giải
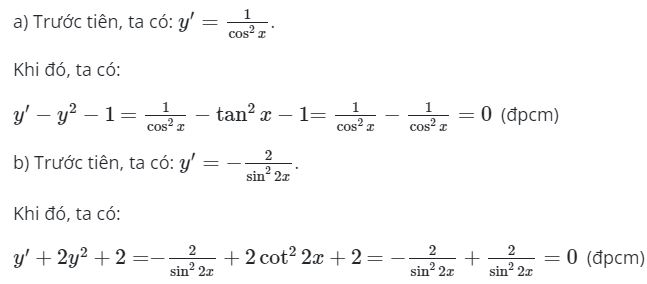
Ví dụ 2: Giải phương trình y’ = 0 trong mỗi trường hợp sau:
a) y = sin 2x – 2cos x.
b) y = 3sin 2x + 4cos 2x + 10x.
Lời giải
a) Trước tiên, ta có: y’ = 2cos 2x + 2sin x.
Khi đó, phương trình có dạng:
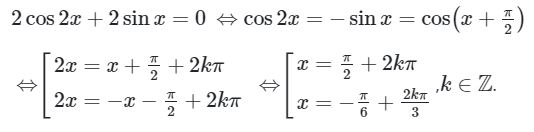
b) Trước tiên, ta có:
y’ = 6cos 2x – 8sin 2x + 10.
Khi đó, phương trình có dạng:
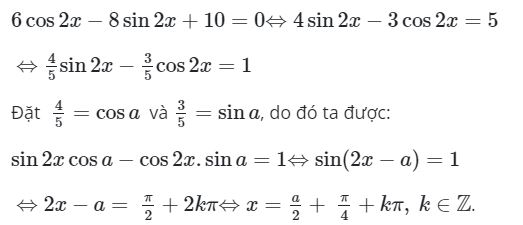
=> Bài viết này với mục đích giúp các bạn HỌC TỐT HƠN với công thức đạo hàm, cũng như là một tài liệu để các bạn dễ dàng ôn luyện lại các kiến thức đã được học một cách đơn giản và đầy đủ nhất, Về công thức đạo hàm lượng giác, công thức đạo hàm nguyên hàm..cơ bản.
Tweet Pin ItTừ khóa » Ct đạo Hàm Ln
-
Bảng đạo Hàm Của Các Hàm Số Cơ Bản (thường Gặp) - MathVn.Com
-
Đạo Hàm Ln - Đạo Hàm Hàm Số Mũ
-
Tổng Hợp Công Thức đạo Hàm Logarit Mũ đầy đủ - Toán Thầy Định
-
Công Thức đạo Hàm: Log, Logarit, Căn Bậc 3, Căn X, Lượng Giác Chuẩn ...
-
Các Công Thức đạo Hàm Của Hàm Mũ Và Logarit - Thầy Phú
-
Bảng đạo Hàm Cơ Bản Và Nâng Cao đầy đủ Nhất
-
Chứng Minh Công Thức đạo Hàm $(\ln U)' = \frac{u'}{u}$?
-
Vì Sao đạo Hàm Của $\ln(x)$ Bằng $\frac{1}{x}$? - Banhoituidap
-
Bảng Công Thức Đạo Hàm Mũ Và Logarit Đầy Đủ, Chính Xác
-
[ĐÚNG NHẤT] Đạo Hàm Của Lnx Là? - Top Lời Giải
-
Top 14 đạo Hàm Ln
-
Đạo Hàm Logarit - đầy đủ Lý Thuyết Và Bài Tập Siêu Chi Tiết
-
Bảng Các Công Thức đạo Hàm Cơ Bản Và Nâng Cao Lớp 11