Công Thức Euler :: Thanhptran

Trang chủ » Công Thức Hàm Euler » Công Thức Euler :: Thanhptran

Có thể bạn quan tâm

Công thức Euler, hay còn gọi là đồng nhất thức Euler, là một công thức toán học trong ngành giải tích phức, được xây dựng bởi nhà toán học người Thụy Sĩ Leonhard Euler. Công thức chỉ ra mối liên hệ giữa hàm số lượng giác và hàm số mũ phức.

Cụ thể, với mọi số thực x, ta có:

e^{ix} = cos(x) + i sin(x) \

Dạng lượng giác của số phức

Định nghĩa

  • Số phức z=a+b*i có thể viết dưới dạng

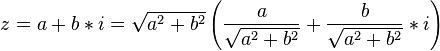z=a+b*i = \sqrt{a^2+b^2}\left(\frac {a}{\sqrt{a^2+b^2}}+\frac {b}{\sqrt{a^2+b^2}}*i \right) hay, khi đặt

r=|z|, \varphi=arg(z),

ta có

z= r(cos \varphi+i\,sin \varphi)

Cách biểu diễn này được gọi là dạng lượng giác của số phức z.

Phép toán trên các số phức viết dưới dạng lượng giác

  • Phép nhân và phép chia các số phức dưới dạng lượng giác

Cho hai số phức dưới dạng lượng giác

z= r(cos \varphi+i\,sin \varphi) z'= r'(cos {\varphi}'+i\,sin {\varphi')}

Khi đó

z*z'= rr'(cos (\varphi+{\varphi}') +i\,sin (\varphi+{\varphi}') \frac {z}{z'}= \frac {r}{r'}(cos (\varphi-{\varphi}') +i\,sin (\varphi-{\varphi}')
  • Lũy thừa tự nhiên của số phức dưới dạng lượng giác (công thức Moirve).
z^n= r^n(cos (n \,\varphi) +i\,sin (n\,\varphi))
  • Khai căn số phức dưới dạng lượng giác.
Mọi số phức z khác 0 đều có đúng n căn bậc n, là các số dạng {\omega}_k=\sqrt[n]{r}(cos {\psi}_k+i\,sin {\psi}_k)

trong đó {\psi}_k = \frac{\varphi+k\,2\,\pi}{n}, k=0,1,...n-1

Từ khóa » Công Thức Hàm Euler