Công Thức Giải Nhanh Trắc Nghiệm Vật Lý 12 ( đầy đủ)

CHƯƠNG I: DAO ĐỘNG CƠ HỌC

I. ĐẠI CƯƠNG VỀ DAO ĐỘNG ĐIỀU HÒA

T: chu kỳ, f: tần số, x: li độ, v: vận tốc, g: gia tốc trọng trường, A: biên độ dao động, \((\omega t+\varphi )\): pha dao động,

\(\varphi\): pha ban đầu, \(\omega\): tốc độ góc.

1. phương trình dao động

- \(x=Acos\left ( \omega t+\varphi \right )\), chu kì: \(T=\frac{2\pi }{\omega }\) , tần số: \(f=\frac{1}{T}=\frac{\omega }{2\pi }\)

- nếu vật thực hiện được N dao động trong thời gian T thì: \(T=\frac{t}{N}; f=\frac{N}{t}\)

2. Phương trình vận tốc

v = x' = \(-\omega Asin(\omega t+\varphi )\)

- x = 0 (VTCB) thì vận tốc cực đại: \(v_{max}=\omega A\)

- x = \(\pm A\) (biên) thì v = 0

3. Phương trình gia tốc

\(a=v'=-\omega ^{2}cos(\omega t+\varphi )=-\omega ^{2}x\)

- x = \(\pm A\) thì \(a_{max}=\omega ^{2}A\)

- x = 0 thì a = 0

Ghi chú: Liên hệ về pha: v sớm pha \(\frac{\pi }{2}\) hơn x, a sớm pha \(\frac{\pi }{2}\) hơn v, a ngược pha với x

4. Hệ thức độc lập thời gian giữa x, v, a

- Giữa x và v: \(A^{2}=x^{2}+\frac{v^{2}}{\omega ^{2}}\)

- giữa v và a: \(v_{max}^{2}=\left ( \omega A \right )^{2}=v^{2}+\frac{a^{2}}{\omega ^{2}}\)

- Giữa a và x: \(a=-\omega ^{2}x\)

5. Các liên hệ khác

- Tốc độ góc: \(\omega =\frac{a_{max}}{v_{max}}\)

- Tính biên độ: \(A=\frac{L}{2}=\frac{S}{4n}=\frac{v_{max}}{\omega }=\frac{v_{max}^{2}}{a_{max}}=\sqrt{\frac{2W}{k}}=\sqrt{x^{2}+\frac{v^{2}}{\omega ^{2}}}=\frac{\sqrt{\omega ^{2}v^{2}+a^{2}}}{\omega ^{2}}\)

6. Tìm pha ban đầu

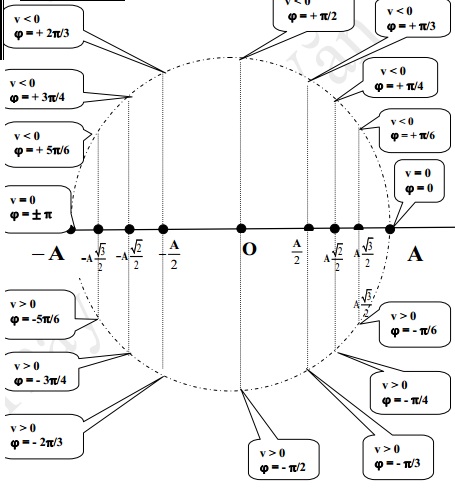
6. Thời gian ngắn nhấtđể vật đi từ:

- \(x_{1}\) đến \(x_{2}\) (giả sử \(x_{1}> x_{2}\)):

\(\Delta t=\frac{\Delta \varphi }{\omega }=\frac{\begin{vmatrix} \varphi _{1}-\varphi _{2} \end{vmatrix}}{\omega }\) với \(\left\{\begin{matrix} cos\varphi _{1}=\frac{x_{1}}{A}\\ cos\varphi _{2}=\frac{x_{2}}{A} \end{matrix}\right. (0\leq\varphi _{1},\varphi _{2}\leq \pi )\)

- \(x_{1}\) đến \(x_{2}\) (giả sử \(x_{1} <x_{2}\)):

\(\Delta t=\frac{\Delta \varphi }{\omega }=\frac{\begin{vmatrix} \varphi _{1}-\varphi _{2} \end{vmatrix}}{\omega }\) với \(\left\{\begin{matrix} cos\varphi _{1}=\frac{x_{1}}{A}\\ cos\varphi _{2}=\frac{x_{2}}{A} \end{matrix}\right. (-\pi \leq\varphi _{1},\varphi _{2}\leq 0 )\)

7. Vận tỗ trung bình - tốc độ trung bình

- Tốc độ trung bình \(V=\frac{S}{t}\)

- Độ dời \(\Delta x\) trong n chu kỳ bằng 0 quãng đường vật đi được trong n chu kỳ bằng \(S=4Na\)

- Vận tốc trung bình \(\overline{v}=\frac{\Delta x}{\Delta t}\)

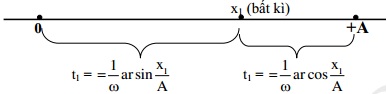
8. Tính quãng đường vật đi được trong thời gian t

- Sơ đồ:

* Công thức giải nhanh tìm quãng đườngùng (dùng máy tính)

.................................................................................................................................................................................

CHƯƠNG VII. HẠT NHÂN NGUYÊN TỬ

I. ĐẠI CƯƠNG VỀ HẠT NHÂN NGUYÊN TỬ

1. Cấu tạo của hạt nhân nguyên tử

- Hạt nhân nguyên tử là phần còn lại của nguyên tử sau khi loại bỏ electron, hạt nhân nguyên tử X kí hiệu là: \(_{Z}^{A}\textrm{X}, XA, ^{A}\textrm{X}\)

Trong đó: Z là nguyên tử số hay số proton trong hạt nhân

                 N là số nơtron \(N= Z+N\)

- kích thước (bán kính) của hạt nhân \(R=1,2.10^{-15}.A^{\frac{1}{3}}\), với A là số khối của hạt nhân.

2. Đơn vị khối lương nguyên tử

- Đơn vị khối nguyên tử là Cacbon (kí hiệu u) \(1u==1,66055.10^{-27}kg\)

- Ngoài ra theo hệ thông chính thức giữa năng lượng và khối lượng anhxtanh, khối lượng còn có thể đo bằng đơn vị \(\frac{eV}{c^{2}}\) hoặc \(\frac{MeV}{c^{2}}\)

\(1u=931,5MeV/c^{2}\)

 

3. Năng lượng liên kết - năng lượng liên kết riêng

Hạt nhân \(_{Z}^{A}\textrm{X}\) có khối lượng m đươc cấu tạo bởi Z hạt proton và N notron. Cho phép đo chính  xác cho thất khối lượng m của hạt nhân \(_{Z}^{A}\textrm{X}\) bao giờ cũng bé hơn tống các khôi lượng của các cuclon tạo thành hạt nhân \(_{Z}^{A}\textrm{X}\): \(\Delta m=Zm_{p}+Nm_{m}-m\) với \(\Delta m\) được gọi là độ gụt khối của hạt nhân.

- Năng lượng liên kết và năng lượng liên kết riêng 

năng lượng liên kết riêng càng lớn thì hạt nhân càng bền vững

- Năng lượng nghỉ: \(E=mc^{2}\) với m là khối lượng nghỉ của hạt nhân

4. Công thức Einstein giữa năng lượng và khối lượng

Năng lượng hạt = Năng lượng nghỉ + Động năng của hạt

                    \(E=E_{0}+E_{d}=mc^{2}+\frac{1}{2}mv^{2}\)

 Bài viết giới thiệu kiến thức chương đầu và cuối của Vật lý 12, Để coi được toàn bộ nội dung bài viết các bạn click vào doawload nha.