Công Thức Hệ Thức Lượng Trong Tam Giác Vuông, Tỉ Số Lượng Giác Của ...

Bài viết này sẽ tổng hợp và hệ thống hóa các công thức lượng giác này một cách chi tiết, giúp các em dễ dàng ghi nhớ và vận dụng để giải các bài tập một cách hiệu quả.

I. Hệ thức về cạnh và đường cao trong tam giác vuông

Xét tam giác vuông  vuông tại , có đường cao . Các cạnh được ký hiệu là , , . Hình chiếu của  và  trên  lần lượt là  và . Đường cao .

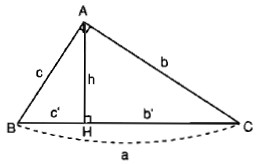
Dựa trên các ký hiệu này, ta có các hệ thức sau:

1.  và

   (Bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.)

2. 

   (Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.)

3. 

   (Tích của cạnh huyền và đường cao tương ứng bằng tích hai cạnh góc vuông.)

4. 

   (Nghịch đảo bình phương đường cao bằng tổng nghịch đảo bình phương của hai cạnh góc vuông.)

II. Định nghĩa tỉ số lượng giác của góc nhọn

Xét góc nhọn  trong một tam giác vuông.

• Cạnh đối: Cạnh đối diện với góc .

• Cạnh kề: Cạnh kề với góc .

• Cạnh huyền: Cạnh đối diện với góc vuông.

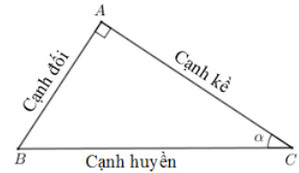
Các tỉ số lượng giác được định nghĩa như sau:

1. sinα = (cạnh đối/cạnh huyền)

2. cosα = (cạnh kề/cạnh huyền)

3. tanα = (cạnh đối/cạnh kề)

4. cotα = (cạnh kề/cạnh đối)

• Mẹo ghi nhớ: "Sin đi học, Cos không hư, Tan đoàn kết, Cot kết đoàn".

(Sin = Đối/Huyền; Cos = Kề/Huyền; Tan = Đối/Kề; Cot - Kề/Đối nên cách nhớ như sau: Sin Đi Học, Cos Không Hư, Tan Đoàn Kết, Cot Kết Đoàn)

III. Tính chất của các tỉ số lượng giác

1. Quan hệ giữa các tỉ số lượng giác

Với một góc nhọn , ta có:

1.  và 

2. 

3. 

4. và

2. Mối quan hệ giữa các góc phụ nhau

Nếu hai góc nhọn  và  phụ nhau (tức là ), ta có:

1. 

2. 

3. 

4. 

IV. Hệ thức về cạnh và góc trong tam giác vuông

Xét tam giác vuông  vuông tại . 

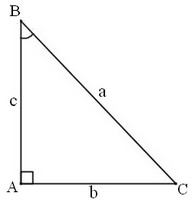
Ta có các hệ thức sau:

1. 

2. 

3. 

4.