[ Công Thức Logarit ] Cơ Bản, Nâng Cao, Định Nghĩa

Trang chủ » Hàm Log » [ Công Thức Logarit ] Cơ Bản, Nâng Cao, Định Nghĩa

Có thể bạn quan tâm

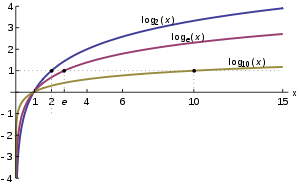
Trong toán học, logarit  là hàm ngược của lũy thừa. Điều đó có nghĩa logarit của một số là số mũ của một giá trị cố định, gọi là cơ số, phải được nâng lên lũy thừa để tạo ra con số đó.

Trong trường hợp đơn giản logarit là đếm số lần lặp đi lặp lại của phép nhân.

Nội Dung

Toggle
  • 1. Công thức Logarit
  • 2. Các bài tập ví dụ về lũy thừa logarit

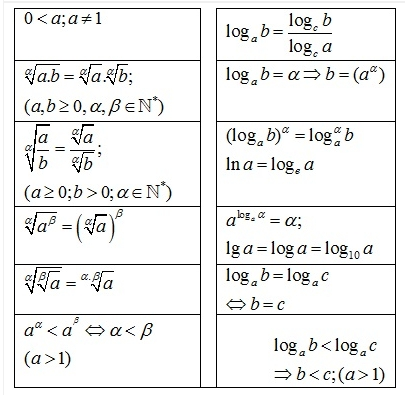
1. Công thức Logarit

=> Ta có công thức logarit như sau: logabα=αlogab điều kiện với mọi số α và a, b là số dương với a # 1.

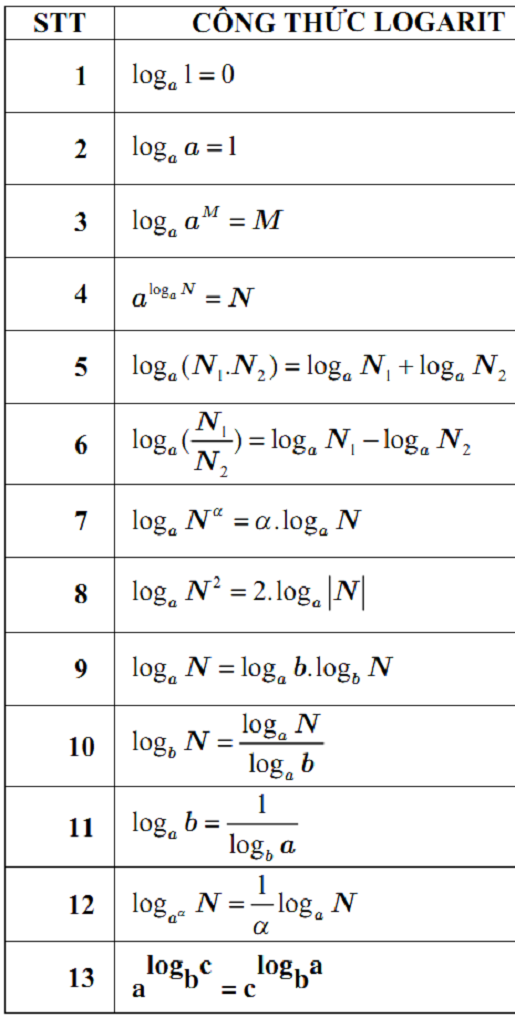
2. Các bài tập ví dụ về lũy thừa logarit

Ví dụ 1: Cho số thực a thõa mãn 0<a≠1. Tính giá trị của biểu thức

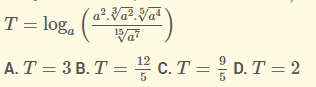
vi du 1

Lời giải chi tiết

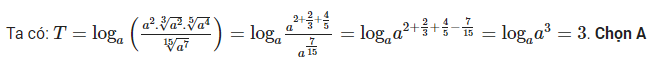
loi giai vi du 1

Ví dụ 2: Cho các số thực a, b, c thõa mãn 1≠a,b,c>0 và các khằng định sau

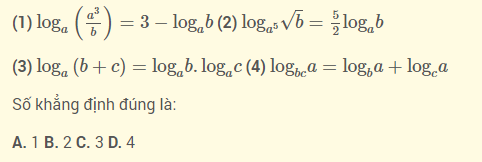
vi du 2

Lời giải chi tiết

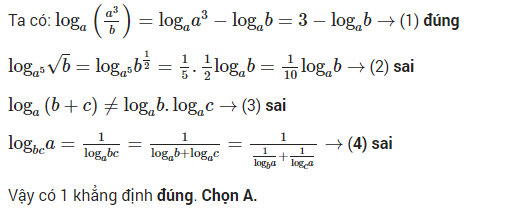
loi giai vi du 2

Ví dụ 3: Cho các số thực a, b, c thõa mãn 1≠a,b,c>0và các khằng định sau

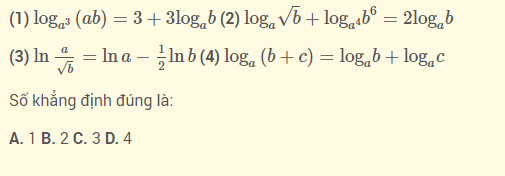
vi du 3

Lời giải chi tiết

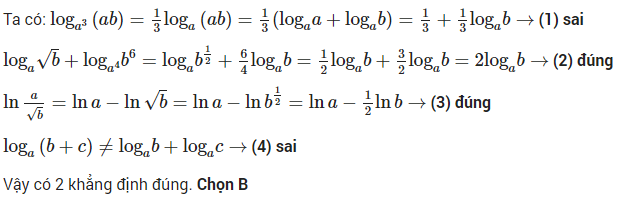
loi giai vi du 3

Ví dụ 4 : Cho các số thực dương và các mệnh đề sau:

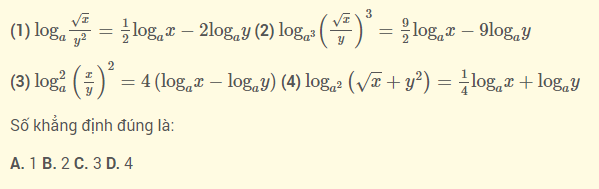
vi du 4

Lời giải chi tiết

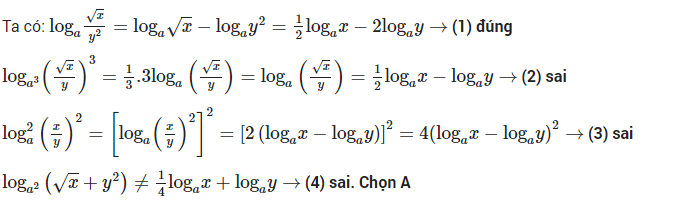
loi giai vi du 4

Bên trên là toàn bộ công thức logarit từ cơ bản đến nâng cao. Mong sẽ giúp được các bạn mỗi khi học đến phần công thức này trên lớp mà chưa hiểu có thể về lại bài online ở đây.

Tweet Pin It

Từ khóa » Hàm Log