Công Thức Logarit đầy đủ, Chi Tiết Nhất – Toán 12

Công thức logarit đầy đủ, chi tiết nhất - Toán lớp 12

1. Lý thuyết Logarit

1. Logarit là gì?

Cho 2 số dương a, b với a≠1. Số x thỏa mãn đẳng thức ax=b được gọi là lôgarit cơ số a của b và kí hiệu là logab

2. Tính chất của Logarit

Với a,b>0; a≠1 ta có

loga1=0logaa=1alogab=blogaaα=α.logaa=α

Bảng tính chất của Logarit

II. Các quy tắc tính Logarit

1. Lôgarit của một tích

- Định lí 1: Với các số dương a, x, y và a≠1 ta có:

logax.y=logax+logay

- Chú ý: Định lí 1 có thể mở rộng cho tích của n số dương:

logax1.x2...xn=logax1+logax2+...+logaxna,xi,i=1,n¯>0; a≠1

2. Lôgarit của một thương

- Định lí 2: Với các số dương a, x, y và a≠1 ta có:

logaxy=logax−logay

3. Lôgarit của một lũy thừa

- Định lí 3: Lôgarit của một lũy thừa bằng tích của số mũ với lôgarit của cơ số.

logabα=α.logaba,b>0; a≠1, α∈ℝ

- Đặc biệt:

logabn=1nlogab

III. Bảng công thức Logarit đầy đủ

1. Công thức Logarit cơ bản

2. Công thức lũy thừa Logarit

3. Công thức đạo hàm Logarit

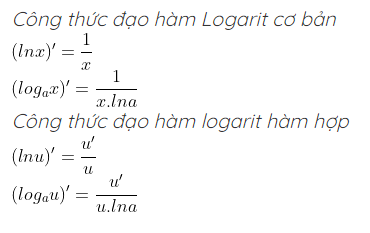
4. Công thức đổi cơ số, lôgarit thập phân và lôgarit tự nhiên

- Cho 3 số dương a, b, c với a≠1, c≠1, ta có:

logab=logcblogca

- Đặc biệt:

logab=1logba      b≠1logaαb=1αlogab    α≠0

- Lôgarit thập phân: Là lôgarit cơ số 10. Kí hiệu: log10x=logx

- Lôgarit tự nhiên: Là lôgarit cơ số e. Kí hiệu: logex=lnx

- Chú ý: Tìm số các chữ số của một lũy thừa:

Bài toán: Số aα có bao nhiêu chữ số?

Số các chữ số của aα chính là logaα+1 (phần nguyên aα cộng 1)

- VD: Số 320 có log320+1=10 chữ số.

IV. Các dạng bài tập về phương trình Logarit và cách giải

Dạng 1. Đưa về cùng cơ số

Xét phương trình cùng cơ số: logaf(x) = logag(x), 0 < a ≠ 1

Bước 1: Nêu điều kiện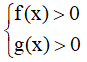

Bước 2 Giải phương trình: logaf(x) = logag(x) ⇔ f(x) = g(x)

Bước 3: So sánh với điều kiện và kết luận.

Ví dụ: Tập nghiệm của phương trình log2(x2- 1) = log2(2x) là

A. {1 + √2}. B. . {2; 41}.

C. {1 + √2; 1 - √2}. D.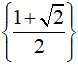

Hướng dẫn giải.

Chọn A.

Điều kiện: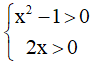Khi đó PT x2- 1 = 2x ⇔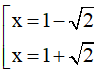

Đối chiếu điều kiện ta được tập nghiệm của phương trình là

Dạng 2. Tìm tập nghiệm của phương trình Logarit bằng cách đặt ẩn phụ

Xét phương trình: f[logag(x)] = 0 (0 < a ≠ 1)

Bước 1: Đặt điều kiện: g(x) > 0

Bước 2: Đặt t = logag(x)

Giải phương trình f(t) = 0, tìm t.

Bước 3: Thay vào phương trình: t = logag(x), tìm x.

Bước 4: Kết hợp với điều kiện và kết luận.

Ví dụ: Nếu đặt t = log2x thì phương trình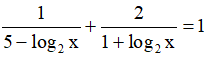 trở thành phương trình nào?

A. t2- 5t + 6 = 0 . B. t2+ 5t + 6 = 0

C. t2- 6t + 5 = 0 D. t2+ 6t + 5 = 0

Hướng dẫn giải

Chọn A

Đặtt = log2x

PT⇔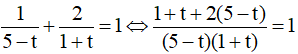 ⇔ 1 + t + 2(5 - t) = (5 - t)(1 + t)

⇔ 11 - t = 5 +4t - t2 ⇔t2- 5t + 6 = 0

Dạng 3. Mũ hóa giải phương trình Logarit

Xét phương trình:logag(x) = f(x) (0 < a ≠ 1)

Bước 1: Đặt điều kiện g(x) > 0

Bước 2: Giải phương trình:

logag(x) = f(x) (0 < a ≠ 1) ⇔g(x) = af(x)

Bước 3: Kết hợp với điều kiện, kết luận nghiệm.

Ví dụ: Phương trình log2(3.2x- 1) = 2x + 1 có bao nhiêu nghiệm?

A. 1. B. 2. C. 3. D. 0.

Hướng dẫn giải

Chọn B.

[Phương pháp tự luận]

Điều kiện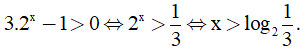

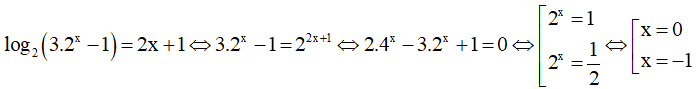
(thỏa mãn).

Vậy phương trình đã cho có 2 nghiệm.

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tínhlog2(3X2x- 1) - 2X - 1

Ấn SHIFT CALC nhập X=5, ấn=. Máy hiệnX=0.

Ấn Alpha X Shift STO A

Ấn AC. Viết lại phương trình: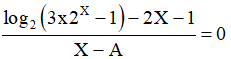

Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi X? Ấn 5 =. Máy hiện X=-1.

Ấn Alpha X Shift STO B.

Ấn AC. Viết lại phương trình: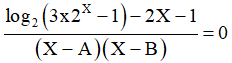

Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi B? Ấn =. Máy hỏi X? Ấn 1=

Máy không giải ra nghiệm. Vậy đã hết nghiệm.

Dạng 4. Dùng đồ thị tìm tập nghiệm của phương trình Logarit

Giải phương trình: logax = f(x) (0 < a ≠ 1) (∗).

Xem phương trình (∗) là phương trình hoành độ giao điểm của hai đồ thị y = logax (0 < a ≠ 1) và y = f(x). Khi đó ta thực hiện hai bước:

Bước 1. Vẽ đồ thị các hàm số y = logax (0 < a ≠ 1) và y = f(x)

Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.

Ví dụ: Phương trình: ln(x2+ x + 1) - ln(2x2+ 1)= x2- x có tổng bình phương các nghiệm bằng:

A. 5 . B. 1 . C. 9 . D. 25 .

Hướng dẫn giải

Chọn B.

Ta có ln(x2+ x + 1) - ln(2x2+ 1)= x2- x

⇔ln(x2+ x + 1) - ln(2x2+ 1)= (2x2+ 1) - (x2+ x + 1)

⇔ln(x2+ x + 1) +(x2+ x + 1) = ln(2x2+ 1)+ (2x2+ 1)

Nhận xét:x2+ x + 1 > 0,∀x ∈ Rvà 2x2+ 1 > 0,∀x ∈ R

Xét hàm số f(t)= lnt + tvới t ∈(0,+∞).

Ta có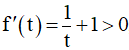, ∀t ∈(0,+∞)nên hàm số f(t)= lnt + t đồng biến trên (0,+∞)

Do đó f(x2+ x + 1) = f(2x2+ 1) ⇔ x2+ x + 1 ⇔ 2x2+ 1 ⇔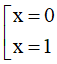

Vậy tổng bình phương các nghiệm là 1 .

V. Các ví dụ minh họa

VD1. Tìm x biết

a. log2x=3

b. 3x=4

c. log3x=4log3a+7log3b

Lời giải:

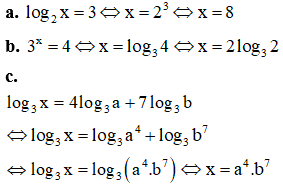
VD2. Cho log25=a. Tính log41250 theo a.

Lời giải:

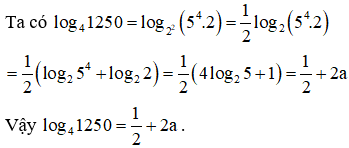
VD3. Cho log315=a và log310=b. Tính log350 theo a và b.

Lời giải:

Ta có:

log350=log31250=2log35.10=2log35+2log310

Ta thấy:

log315=a⇔1+log35=a⇒log35=a−1

Thay lại ta được:

log350=2a−1+2b⇔log350=2a+2b−2

VD4. Cho a=log23, b=log35, c=log72. Tính log14063 theo a, b, c

Lời giải:

Ta có:

log14063=log763log7140=log732.7log722.5.7=1+2log731+2log72+log75

+) log73=log23.log72=a.c

+) log75=log35.log73=b.a.c

Thay vào ta được:

log14063=1+2ac1+2c+abc

VI. Bài tập vận dụng

Bài 1. Tính

a. log218

b. log142

c. log334

Bài 2. Tính

a. 4log25

b. 27−log92

c. 9log32

Bài 3. Tính

a. A=12log736−log714−3log7213

b. B=log224−12log272log318−13log372

Bài 4. Tìm x biết

a. log5x=2log5a−3log5ba,b>0

b. log12x=23log12a−15log12ba,b>0

Bài 5. So sánh các cặp số sau

a. log35 và log74

b. log210 và log530

Bài 6.

a. log25=a và log35=b. Tính log65 theo a và b

b. Cho log23=a; log53=b. Hãy biểu diễn log645 theo a và b.

Xem thêm tổng hợp công thức môn Toán lớp 12 đầy đủ và chi tiết khác:

Công thức lũy thừa đầy đủ, chi tiết nhất

Công thức tính lãi suất ngân hàng Toán 12 chi tiết nhất

Công thức giải phương trình mũ đầy đủ, chi tiết nhất

Công thức giải bất phương trình mũ chi tiết nhất

Công thức giải phương trình lôgarit chi tiết nhất