Công Thức Phân Tán Của Một Biến Ngẫu Nhiên. Phương Sai Và độ ...

Trang chủ » Tính Kỳ Vọng Và Phương Sai Trong Excel » Công Thức Phân Tán Của Một Biến Ngẫu Nhiên. Phương Sai Và độ ...

Có thể bạn quan tâm

Tuy nhiên, chỉ riêng đặc điểm này thôi thì chưa đủ để nghiên cứu biến ngẫu nhiên. Hãy tưởng tượng hai tay súng đang bắn vào một mục tiêu. Một người bắn chính xác và đánh gần trung tâm, và người kia ... chỉ vui vẻ và thậm chí không nhắm mục tiêu. Nhưng điều buồn cười là trung bình kết quả sẽ giống hệt như game bắn súng đầu tiên! Tình huống này được minh họa có điều kiện bởi các biến ngẫu nhiên sau:

"Kẻ bắn tỉa" gia trị được ki vọng là bình đẳng, tuy nhiên, và tính cách thú vị»: - nó cũng bằng không!

Do đó, cần phải định lượng bao xa rải rác dấu đầu dòng (giá trị của một biến ngẫu nhiên) so với tâm của mục tiêu (kỳ vọng). tốt và phân tán chỉ dịch từ tiếng Latinh là sự phân tán .

Hãy xem đặc tính số này được xác định như thế nào trong một trong các ví dụ của phần 1 của bài học:

Ở đó, chúng tôi đã tìm thấy một kỳ vọng toán học đáng thất vọng về trò chơi này và bây giờ chúng tôi phải tính toán phương sai của nó, biểu thị bởi vì .

Hãy cùng tìm hiểu xem số tiền thắng / thua "phân tán" bao xa so với giá trị trung bình. Rõ ràng, đối với điều này, chúng ta cần tính toán sự khác biệtở giữa giá trị của một biến ngẫu nhiên và cô ấy kỳ vọng toán học:

–5 – (–0,5) = –4,5 2,5 – (–0,5) = 3 10 – (–0,5) = 10,5

Bây giờ có vẻ là cần thiết để tổng hợp các kết quả, nhưng cách này không tốt - vì lý do là các dao động bên trái sẽ triệt tiêu lẫn nhau với các dao động bên phải. Vì vậy, chẳng hạn, game bắn súng "nghiệp dư" (ví dụ trên) sự khác biệt sẽ là , và khi được thêm vào, chúng sẽ cho kết quả bằng không, vì vậy chúng tôi sẽ không ước tính được bất kỳ sự phân tán của vụ bắn súng của anh ta.

Để giải quyết vấn đề khó chịu này, hãy xem xét mô-đun sự khác biệt, nhưng vì lý do kỹ thuật, cách tiếp cận đã bắt nguồn từ khi chúng được bình phương. Sẽ thuận tiện hơn khi sắp xếp giải pháp trong một bảng: Và ở đây nó yêu cầu tính toán bình quân gia quyền giá trị của độ lệch bình phương. Nó là gì? Nó là của họ gia trị được ki vọng, là thước đo của sự tán xạ:

– Định nghĩa sự phân tán. Rõ ràng ngay lập tức từ định nghĩa rằng phương sai không thể âm- lưu ý để luyện tập!

Hãy nhớ cách tìm kỳ vọng. Nhân các chênh lệch bình phương với các xác suất tương ứng (Tiếp tục bảng):- nói một cách hình tượng thì đây là "lực kéo", và tóm tắt kết quả:

Bạn không nghĩ rằng dựa trên nền tảng của chiến thắng, kết quả hóa ra là quá lớn? Đúng vậy - chúng tôi đã bình phương, và để quay lại thứ nguyên của trò chơi, chúng tôi cần lấy căn bậc hai. Giá trị này triệu tập độ lệch chuẩn và được ký hiệu bằng chữ cái Hy Lạp "sigma":

Đôi khi ý nghĩa này được gọi là độ lệch chuẩn .

Ý nghĩa của nó là gì? Nếu chúng ta đi chệch khỏi kỳ vọng toán học sang trái và sang phải theo giá trị trung bình độ lệch chuẩn:- thì các giá trị có thể xảy ra nhất của biến ngẫu nhiên sẽ được “tập trung” vào khoảng này. Những gì chúng ta đang thực sự thấy:

Tuy nhiên, nó đã xảy ra như vậy là trong phân tích sự tán xạ hầu như luôn hoạt động với khái niệm phân tán. Hãy xem nó có ý nghĩa gì trong mối quan hệ với trò chơi. Nếu trong trường hợp của game bắn súng chúng ta đang nói về "độ chính xác" của các cú đánh so với tâm của mục tiêu, thì ở đây sự phân tán đặc trưng cho hai điều:

Đầu tiên, rõ ràng là khi tỷ lệ tăng, phương sai cũng tăng. Vì vậy, ví dụ, nếu chúng ta tăng lên 10 lần, thì kỳ vọng toán học sẽ tăng lên 10 lần và phương sai sẽ tăng lên 100 lần (ngay khi nó là giá trị bậc hai). Nhưng lưu ý rằng luật chơi không thay đổi! Chỉ có tỷ lệ đã thay đổi, nói một cách đại khái, chúng tôi từng đặt cược 10 rúp, bây giờ là 100.

Thứ hai, hơn thế nữa điểm thú vị là phương sai đặc trưng cho phong cách của trò chơi. Tinh thần cố định tỷ lệ trò chơi ở một số cấp độ nhất định và xem những gì ở đây:

Một trò chơi có phương sai thấp là một trò chơi thận trọng. Người chơi có xu hướng chọn các kế hoạch đáng tin cậy nhất, nơi anh ta không thua / thắng quá nhiều cùng một lúc. Ví dụ, hệ thống đỏ / đen trong roulette (xem Ví dụ 4 của bài báo biến ngẫu nhiên) .

Trò chơi có phương sai cao. Cô ấy thường được gọi là sự phân tán trò chơi. Đây là một phong cách chơi mạo hiểm hoặc hung hãn, trong đó người chơi chọn các sơ đồ "adrenaline". Ít nhất hãy nhớ "Martingale", trong đó tổng số tiền đặt cược là các đơn hàng có độ lớn lớn hơn trò chơi "yên tĩnh" của đoạn trước.

Tình huống trong poker là một dấu hiệu: có những cái gọi là chặt những người chơi có xu hướng thận trọng và "run" với quỹ trò chơi của họ (danh sách ngân hàng). Không có gì ngạc nhiên khi ngân hàng của họ không dao động nhiều (phương sai thấp). Ngược lại, nếu một người chơi có phương sai cao, thì đó là kẻ xâm lược. Anh ta thường chấp nhận rủi ro, đặt cược lớn và có thể phá vỡ một ngân hàng khổng lồ và chia thành từng mảnh.

Điều tương tự cũng xảy ra trong Forex, v.v. - có rất nhiều ví dụ.

Hơn nữa, trong mọi trường hợp, không quan trọng trò chơi là một xu hay hàng nghìn đô la. Mỗi cấp độ đều có những người chơi có phương sai thấp và cao. Vâng, đối với chiến thắng trung bình, như chúng ta nhớ, "có trách nhiệm" gia trị được ki vọng.

Bạn có thể nhận thấy rằng việc tìm ra phương sai là một quá trình lâu dài và vất vả. Nhưng toán học rất hào phóng:

Công thức tìm phương sai

Công thức này bắt nguồn trực tiếp từ định nghĩa của phương sai, và chúng tôi ngay lập tức đưa nó vào lưu thông. Tôi sẽ sao chép đĩa với trò chơi của chúng tôi từ phía trên: và kỳ vọng được tìm thấy.

Chúng tôi tính phương sai theo cách thứ hai. Đầu tiên, chúng ta hãy tìm kỳ vọng toán học - bình phương của biến ngẫu nhiên. Qua định nghĩa về kỳ vọng toán học:

TẠI trường hợp này:

Như vậy, theo công thức:

Như họ nói, hãy cảm nhận sự khác biệt. Và trong thực tế, tất nhiên, tốt hơn là áp dụng công thức (trừ khi điều kiện yêu cầu khác).

Chúng tôi nắm vững kỹ thuật giải quyết và thiết kế:

Ví dụ 6

Tìm kỳ vọng toán học, phương sai và độ lệch chuẩn của nó.

Nhiệm vụ này được tìm thấy ở khắp mọi nơi, và như một quy luật, không có ý nghĩa rõ ràng. Bạn có thể tưởng tượng một số bóng đèn với các con số sáng lên trong một nhà thương điên với một số xác suất nhất định :)

Quyết định: Thật tiện lợi khi tóm tắt các phép tính chính trong một bảng. Đầu tiên, chúng tôi viết dữ liệu ban đầu trong hai dòng trên cùng. Sau đó, chúng tôi tính toán các sản phẩm, sau đó và cuối cùng là tổng trong cột bên phải:

Trên thực tế, hầu hết mọi thứ đã sẵn sàng. Trong dòng thứ ba, một kỳ vọng toán học được tạo sẵn đã được rút ra: .

Độ phân tán được tính theo công thức:

Và cuối cùng, độ lệch chuẩn: - Riêng tôi, tôi thường làm tròn đến 2 chữ số thập phân.

Tất cả các phép tính có thể được thực hiện trên máy tính và thậm chí còn tốt hơn - trong Excel:

Thật khó để làm sai ở đây :)

Trả lời:

Những người mong muốn có thể đơn giản hóa cuộc sống của họ hơn nữa và tận dụng lợi thế của tôi máy tính (thử nghiệm), điều này sẽ không chỉ giải quyết ngay lập tức nhiệm vụ này, mà còn xây dựng đồ họa chuyên đề (đến sớm). Chương trình có thể tải xuống trong thư viện- nếu bạn đã tải xuống ít nhất một Tài liệu giáo dục hoặc nhận được cách khác. Cảm ơn đã ủng hộ dự án!

Một số nhiệm vụ cho giải pháp độc lập:

Ví dụ 7

Tính phương sai của biến ngẫu nhiên của ví dụ trước theo định nghĩa.

Và một ví dụ tương tự:

Ví dụ 8

Một biến ngẫu nhiên rời rạc được cho bởi luật phân phối của chính nó:

Có, các giá trị của biến ngẫu nhiên có thể khá lớn (ví dụ từ công việc thực sự) và ở đây, nếu có thể, hãy sử dụng Excel. Nhân tiện, trong Ví dụ 7 - nó nhanh hơn, đáng tin cậy hơn và dễ chịu hơn.

Giải pháp và câu trả lời ở cuối trang.

Cuối phần 2 của bài, chúng ta sẽ phân tích thêm một nhiệm vụ điển hình, người ta thậm chí có thể nói, một xe buýt nhỏ:

Ví dụ 9

Một biến ngẫu nhiên rời rạc chỉ có thể nhận hai giá trị: và, và. Xác suất, kỳ vọng toán học và phương sai đã được biết.

Quyết định: Hãy bắt đầu với một xác suất chưa biết. Vì một biến ngẫu nhiên chỉ có thể nhận hai giá trị, nên tổng xác suất của các sự kiện tương ứng:

và kể từ đó .

Nó vẫn còn để tìm ..., dễ dàng để nói :) Nhưng ôi thôi, nó đã bắt đầu. Theo định nghĩa của kỳ vọng toán học: - thay thế các giá trị đã biết:

- và không có gì khác có thể được loại bỏ khỏi phương trình này, ngoại trừ việc bạn có thể viết lại nó theo hướng thông thường:

hoặc:

O bước tiếp theo Tôi nghĩ bạn có thể đoán được. Hãy tạo và giải quyết hệ thống:

Số thập phân- điều này, tất nhiên, là một sự ô nhục hoàn toàn; nhân cả hai phương trình với 10:

và chia cho 2:

Tốt hơn nhiều. Từ phương trình thứ nhất, chúng ta biểu thị: (đây là cách dễ dàng hơn)- thay thế trong phương trình thứ 2:

Chúng tôi đang xây dựng bình phương và đơn giản hóa: Chúng tôi nhân với:

Kết quả là, phương trình bậc hai, tìm điểm phân biệt của nó: - hoàn hảo!

và chúng tôi nhận được hai giải pháp:

1) nếu , sau đó ;

2) nếu , sau đó .

Cặp giá trị đầu tiên thỏa mãn điều kiện. Với xác suất cao, mọi thứ đều đúng, tuy nhiên, chúng tôi viết ra luật phân phối: và thực hiện kiểm tra, cụ thể là tìm kỳ vọng:

Trong nhiều trường hợp, nó trở nên cần thiết để giới thiệu một đặc tính sốđể đo mức độ sự phân tán, sự lan tỏa của các giá trị, được coi là một biến ngẫu nhiên ξ , xung quanh kỳ vọng toán học của nó.

Sự định nghĩa. Phương sai của một biến ngẫu nhiên ξ được gọi là một số.

D= M (ξ-M ξ) 2 . (1)

Nói cách khác, độ phân tán là kỳ vọng toán học về độ lệch bình phương của các giá trị của một biến ngẫu nhiên so với giá trị trung bình của nó.

triệu tập hình vuông có nghĩa là lệch lạc

số lượng ξ .

Nếu sự phân tán đặc trưng kích thước trung bìnhĐộ lệch bình phương ξ từ Mξ, thì con số có thể được coi là một số đặc điểm trung bìnhđộ lệch của chính nó, chính xác hơn là độ lớn của | ξ-Mξ |.

Định nghĩa (1) ngụ ý hai tính chất sau đây của sự phân tán.

1. Sự phân tán giá trị hiện có bằng không. Điều này khá phù hợp với ý nghĩa trực quan của sự phân tán, như một "thước đo của sự lan truyền".

Thật vậy, nếu

ξ \ u003d C, sau đó Mξ = C và điều đó có nghĩa là Dξ = M (C-C) 2 = M 0 = 0.

2. Khi nhân một biến ngẫu nhiên ξ trên số không đổi Với phương sai của nó được nhân với C 2

D (Cξ) = C 2 Dξ . (3)

Thật sự

D (Cξ) = M (C

= M (C .

3. Có công thức tính phương sai sau:

. (4)

Việc chứng minh công thức này dựa trên các thuộc tính của kỳ vọng toán học.

Chúng ta có:

4. Nếu các giá trị ξ 1 và ξ 2 là độc lập, khi đó phương sai của tổng của chúng bằng tổng phương sai của chúng:

Bằng chứng . Để chứng minh, chúng tôi sử dụng các tính chất của kỳ vọng toán học. Để cho được Mξ 1 = m 1 , Mξ 2 = m 2 sau đó.

Công thức (5) được chứng minh.

Vì phương sai của một biến ngẫu nhiên, theo định nghĩa, là kỳ vọng toán học của giá trị ( ξ-m) 2, ở đâu m = Mξ, sau đó để tính phương sai, bạn có thể sử dụng các công thức thu được trong Mục 7, Chương II.

Vì vậy nếu ξ có một DSV với luật phân phối

x 1 x 2 ...
P 1 P 2 ...

thì chúng ta sẽ có:

. (7)

Nếu một ξ biến ngẫu nhiên liên tục với mật độ phân phối p (x), sau đó chúng tôi nhận được:

Dξ= . (8)

Nếu công thức (4) được sử dụng để tính phương sai, thì có thể thu được các công thức khác, đó là:

, (9)

nếu giá trị ξ rời rạc, và

Dξ= , (10)

nếu ξ phân phối với mật độ P(x).

Ví dụ 1 . Hãy để giá trị ξ được phân bố đồng đều trên khoảng [ a, b]. Sử dụng công thức (10), chúng tôi nhận được:

Có thể chứng minh rằng phương sai của một biến ngẫu nhiên phân bố theo quy luật chuẩn với mật độ

p (x)= , (11)

bằng σ 2.

Điều này làm rõ ý nghĩa của tham số σ có trong biểu thức mật độ (11) đối với luật bình thường; σ có một mức trung bình độ lệch chuẩn số lượng ξ.

Ví dụ 2. Tìm phương sai của một biến ngẫu nhiên ξ phân phối theo luật nhị thức.

Quyết định . Sử dụng biểu diễn của ξ trong biểu mẫu

ξ = ξ 1 + ξ 2 + N(xem ví dụ 2 §7 ch. II) và áp dụng công thức thêm phương sai cho biến độc lập, chúng tôi nhận được

Dξ = Dξ 1 + Dξ 2 + Dξn .

Sự phân tán của bất kỳ số lượng nào ξi (tôi= 1,2, N) được tính trực tiếp:

Dξi = M (ξi) 2 - (Tôi) 2 = 0 2 q+ 1 2 P- P 2 = P(1-P) = pq.

Cuối cùng chúng tôi nhận được

Dξ= npq, ở đâu q = 1 -P.

Đối với dữ liệu được nhóm sự phân tán còn lại - Trung bình của phương sai trong nhóm:

Trong đó σ 2 j là phương sai trong nhóm của nhóm thứ j.

Đối với dữ liệu chưa được nhóm sự phân tán còn lại là thước đo độ chính xác gần đúng, tức là xấp xỉ của đường hồi quy với dữ liệu ban đầu: trong đó y (t) là dự báo theo phương trình xu hướng; y t - chuỗi động lực học ban đầu; n là số điểm; p là số hệ số của phương trình hồi quy (số biến giải thích). Trong ví dụ này, nó được gọi là ước tính không thiên vị của phương sai.

Ví dụ 1. Sự phân bố công nhân của ba xí nghiệp của một hiệp hội theo các loại thuế quan được đặc trưng bởi dữ liệu sau:

Mức lương của người lao độngSố lượng công nhân tại doanh nghiệp
doanh nghiệp 1xí nghiệp 2xí nghiệp 3
1 50 20 40
2 100 80 60
3 150 150 200
4 350 300 400
5 200 150 250
6 150 100 150

Định nghĩa: 1. phân tán cho mỗi doanh nghiệp (phân tán trong nhóm); 2. trung bình của sự phân tán trong nhóm; 3. sự phân tán giữa các nhóm; 4. tổng phương sai.

Quyết định. Trước khi tiến hành giải, cần tìm hiểu tính năng nào là hiệu quả và tính năng nào là giai thừa. Trong ví dụ đang xem xét, đặc điểm hiệu quả là "Loại biểu thuế", và đặc điểm hệ số là "Số (tên) doanh nghiệp". Sau đó, chúng ta có ba nhóm (doanh nghiệp) mà cần phải tính toán phương sai trung bình của nhóm và phương sai trong nhóm:

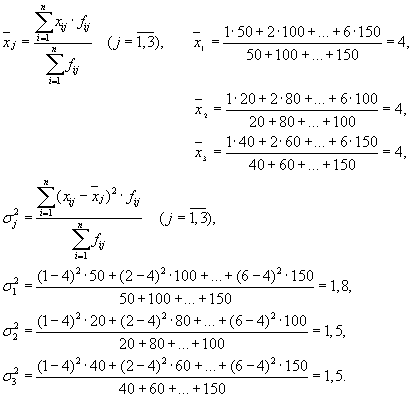
Công tytrung bình của nhóm,phương sai trong nhóm,
1 4 1,8
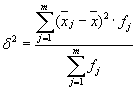
Giá trị trung bình của các phương sai trong nhóm ( sự phân tán còn lại) được tính theo công thức:

nơi bạn có thể tính toán: hoặc:

sau đó: Tổng độ phân tán sẽ bằng: s 2 \ u003d 1.6 + 0 \ u003d 1.6. Tổng phương sai cũng có thể được tính bằng một trong hai công thức sau:

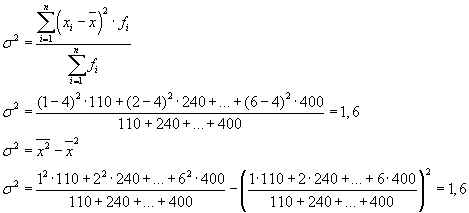
Khi giải các bài toán thực tế, người ta thường phải xử lý một dấu hiệu mà chỉ nhận hai giá trị thay thế. Trong trường hợp này, họ không nói về trọng lượng của một giá trị cụ thể của một đối tượng địa lý, mà là về tỷ trọng của nó trong tổng thể. Nếu tỷ lệ các đơn vị dân số có đặc điểm đang nghiên cứu được ký hiệu là " R", và không sở hữu - thông qua" q”, Thì độ phân tán có thể được tính theo công thức: s 2 = p × q

Ví dụ # 2. Dựa trên dữ liệu về sản lượng của sáu công nhân của lữ đoàn, xác định phương sai giữa các nhóm và đánh giá tác động của sự thay đổi công việc đến năng suất lao động của họ nếu tổng phương sai là 12,2.

Số của lữ đoàn làm việcSản lượng làm việc, chiếc.
trong ca đầu tiêntrong ca thứ 2
1 18 13
2 19 14
3 22 15
4 20 17
5 24 16
6 23 15

Quyết định. Dữ liệu ban đầu

Xf1f2f 3f4f5f6Toàn bộ
1 18 19 22 20 24 23 126
2 13 14 15 17 16 15 90
Toàn bộ 31 33 37 37 40 38
Sau đó, chúng ta có 6 nhóm mà cần phải tính giá trị trung bình của nhóm và phương sai nội nhóm. 1. Tìm các giá trị trung bình của mỗi nhóm.2. Tìm bình phương trung bình của mỗi nhóm.Chúng tôi tóm tắt kết quả của phép tính trong một bảng:
Số nhómNhóm trung bìnhPhương sai nội nhóm
1 1.42 0.24
2 1.42 0.24
3 1.41 0.24
4 1.46 0.25
5 1.4 0.24
6 1.39 0.24
3. Phương sai nội nhómđặc trưng cho sự thay đổi (sự biến đổi) của tính trạng được nghiên cứu (kết quả) trong nhóm dưới tác động của tất cả các yếu tố, ngoại trừ yếu tố cơ bản của việc phân nhóm: Chúng tôi tính giá trị trung bình của sự phân tán trong nhóm bằng công thức: 4. Phương sai giữa các nhómđặc trưng cho sự thay đổi (sự biến đổi) của tính trạng được nghiên cứu (kết quả) dưới tác động của một yếu tố (đặc điểm giai thừa) nằm trong nhóm. Sự phân tán giữa các nhóm được định nghĩa là: ở đâu sau đó Tổng phương saiđặc trưng cho sự thay đổi (sự biến đổi) của tính trạng được nghiên cứu (kết quả) dưới tác động của tất cả các yếu tố (tính trạng giai thừa) mà không có ngoại lệ. Theo điều kiện của bài toán, nó bằng 12,2. Mối quan hệ tương quan thực nghiệmđo lường mức độ biến động tổng số của thuộc tính kết quả do nhân tố được nghiên cứu gây ra. Đây là tỷ lệ giữa phương sai giai thừa trên tổng phương sai: Chúng tôi xác định mối quan hệ tương quan thực nghiệm: Mối quan hệ giữa các đối tượng địa lý có thể yếu hoặc mạnh (gần gũi). Tiêu chí của họ được đánh giá trên thang điểm Chaddock: 0,1 0,3 0,5 0,7 0,9 Trong ví dụ của chúng tôi, mối quan hệ giữa đặc điểm Y yếu tố X là yếu Hệ số xác định. Hãy xác định hệ số xác định: Như vậy, 0,67% sự biến đổi là do sự khác biệt giữa các tính trạng và 99,37% là do các yếu tố khác. Sự kết luận: trong trường hợp này, sản lượng của người lao động không phụ thuộc vào công việc trong một ca cụ thể, tức là ảnh hưởng của việc dịch chuyển công việc đến năng suất lao động của họ là không đáng kể và còn do các yếu tố khác.

Ví dụ # 3. Dựa trên mức trung bình tiền công và bình phương độ lệch so với giá trị của nó cho hai nhóm công nhân, tìm tổng phương sai bằng cách áp dụng quy tắc thêm phương sai:

Quyết định: Trung bình của các phương sai trong nhóm Sự phân tán giữa các nhóm được định nghĩa là: Tổng phương sai sẽ là: 480 + 13824 = 14304

Các chỉ số tổng quát chính của sự biến động trong thống kê là độ phân tán và độ lệch chuẩn.

Sự phân tán nó trung bình cộng độ lệch bình phương của từng giá trị đối tượng so với tổng giá trị trung bình. Phương sai thường được gọi là bình phương trung bình của độ lệch và được ký hiệu là  2. Tùy thuộc vào dữ liệu ban đầu, phương sai có thể được tính từ trung bình cộng, đơn giản hoặc trọng số:

 phân tán không trọng lượng (đơn giản);

 phương sai có trọng số.

Độ lệch chuẩn là đặc điểm tổng quát của kích thước tuyệt đối các biến thể đặc điểm trong tổng hợp. Nó được thể hiện bằng các đơn vị tương tự như dấu hiệu (mét, tấn, phần trăm, hecta, v.v.).

Độ lệch chuẩn là căn bậc hai của phương sai và được ký hiệu là :

 độ lệch chuẩn không trọng số;

 độ lệch chuẩn có trọng số.

Độ lệch chuẩn là thước đo độ tin cậy của giá trị trung bình. Độ lệch chuẩn càng nhỏ, giá trị trung bình số học phản ánh toàn bộ tổng thể được đại diện càng tốt.

Việc tính toán độ lệch chuẩn được đặt trước bằng việc tính toán phương sai.

Quy trình tính phương sai có trọng số như sau:

1) xác định giá trị trung bình cộng:

2) tính toán độ lệch của các tùy chọn so với mức trung bình:

3) bình phương độ lệch của mỗi tùy chọn so với giá trị trung bình:

4) nhân độ lệch bình phương với trọng số (tần số):

5) tóm tắt các tác phẩm đã nhận:

6) số tiền thu được chia cho tổng trọng số:

Ví dụ 2.1

Tính giá trị trung bình cộng:

Các giá trị của độ lệch so với giá trị trung bình và bình phương của chúng được trình bày trong bảng. Hãy xác định phương sai:

Độ lệch chuẩn sẽ bằng:

Nếu dữ liệu nguồn được trình bày dưới dạng khoảng thời gian loạt phân phối , thì trước tiên bạn cần xác định giá trị rời rạc của đối tượng, rồi áp dụng phương pháp được mô tả.

Ví dụ 2.2

Hãy để chúng tôi trình bày phép tính phương sai cho chuỗi khoảng thời gian trên dữ liệu về sự phân bố diện tích gieo hạt của trang trại tập thể theo năng suất lúa mì.

Trung bình cộng là:

Hãy tính phương sai:

6.3. Tính toán độ phân tán theo công thức cho dữ liệu riêng lẻ

Kỹ thuật tính toán sự phân tán phức tạp, và giá trị lớn các tùy chọn và tần số có thể cồng kềnh. Tính toán có thể được đơn giản hóa bằng cách sử dụng các thuộc tính phân tán.

Sự phân tán có các tính chất sau.

1. Sự giảm hoặc tăng trọng số (tần số) của một đối tượng địa lý biến đổi một số lần nhất định không làm thay đổi độ phân tán.

2. Giảm hoặc tăng từng giá trị tính năng theo cùng một giá trị không đổi NHƯNGđộ phân tán không thay đổi.

3. Giảm hoặc tăng từng giá trị tính năng lên một số lần nhất định k tương ứng làm giảm hoặc tăng phương sai trong k 2 lần độ lệch chuẩn  trong k Một lần.

4. Phương sai của một đối tượng so với một giá trị tùy ý luôn lớn hơn phương sai so với giá trị trung bình cộng bình phương của hiệu giữa giá trị trung bình và giá trị tùy ý:

Nếu một NHƯNG 0, khi đó chúng ta đạt đến đẳng thức sau:

tức là, phương sai của một đối tượng địa lý bằng hiệu giữa bình phương trung bình của các giá trị đối tượng địa lý và bình phương giá trị trung bình.

Mỗi thuộc tính có thể được sử dụng một mình hoặc kết hợp với các thuộc tính khác khi tính phương sai.

Quy trình tính toán phương sai rất đơn giản:

1) xác định trung bình cộng :

2) Bình phương trung bình số học:

3) bình phương độ lệch của mỗi biến thể của chuỗi:

X tôi 2 .

4) tìm tổng bình phương của các lựa chọn:

5) chia tổng bình phương của các lựa chọn cho số của chúng, tức là xác định bình phương trung bình:

6) xác định sự khác biệt giữa bình phương trung bình của đối tượng địa lý và bình phương trung bình:

Ví dụ 3.1 Chúng tôi có dữ liệu sau đây về năng suất của người lao động:

Hãy thực hiện các phép tính sau:

Độ phân tán của một biến ngẫu nhiên là thước đo mức độ lan truyền các giá trị của biến này. Phương sai nhỏ có nghĩa là các giá trị được nhóm gần nhau. Một phương sai lớn cho thấy sự phân tán giá trị mạnh mẽ. Khái niệm về độ phân tán của một biến ngẫu nhiên được sử dụng trong thống kê. Ví dụ, nếu bạn so sánh phương sai của các giá trị của hai đại lượng (chẳng hạn như kết quả quan sát bệnh nhân nam và bệnh nhân nữ), bạn có thể kiểm tra ý nghĩa của một số biến. Phương sai cũng được sử dụng trong xây dựng mô hình thống kê, vì một phương sai nhỏ có thể là một dấu hiệu cho thấy bạn đang trang bị quá mức các giá trị.

Các bước

Tính toán phương sai mẫu

  1. Ghi lại các giá trị mẫu. Trong hầu hết các trường hợp, chỉ các mẫu của một số quần thể nhất định mới có sẵn cho các nhà thống kê. Ví dụ: theo quy định, các nhà thống kê không phân tích chi phí duy trì tổng thể của tất cả các xe ô tô ở Nga - họ phân tích mẫu thử ngẫu nhiên từ vài nghìn chiếc. Một mẫu như vậy sẽ giúp xác định chi phí trung bình cho mỗi chiếc ô tô, nhưng rất có thể, giá trị thu được sẽ khác xa so với giá trị thực.

    • Ví dụ, hãy phân tích số lượng bánh bán được ở một quán cà phê trong 6 ngày, được lấy theo thứ tự ngẫu nhiên. Mẫu có lần xem tiếp theo: 17, 15, 23, 7, 9, 13. Đây là mẫu, không phải dân số, vì chúng tôi không có dữ liệu về bánh được bán cho mỗi ngày quán cà phê mở cửa.
    • Nếu bạn được cung cấp một tập hợp chứ không phải một mẫu giá trị, hãy chuyển sang phần tiếp theo.

  2. Viết công thức tính phương sai mẫu.Độ phân tán là thước đo sự lan truyền các giá trị của một đại lượng nào đó. Giá trị phân tán càng gần bằng 0, các giá trị được nhóm lại với nhau càng gần. Khi làm việc với một mẫu giá trị, hãy sử dụng công thức sau để tính phương sai:

    • s 2 (\ displaystyle s ^ (2)) = ∑[(x i (\ displaystyle x_ (i))-x̅) 2 (\ displaystyle ^ (2))] / (n - 1)
    • s 2 (\ displaystyle s ^ (2)) là sự phân tán. Độ phân tán được đo bằng đơn vị hình vuôngđo.
    • x i (\ displaystyle x_ (i))- mỗi giá trị trong mẫu.
    • x i (\ displaystyle x_ (i)) bạn cần trừ x̅, bình phương nó, và sau đó cộng các kết quả.
    • x̅ - giá trị trung bình của mẫu (sample mean).
    • n là số giá trị trong mẫu.

  3. Tính giá trị trung bình của mẫu. Nó được ký hiệu là x̅. Giá trị trung bình của mẫu được tính giống như trung bình cộng thông thường: cộng tất cả các giá trị trong mẫu, sau đó chia kết quả cho số giá trị trong mẫu.

    • Trong ví dụ của chúng tôi, hãy thêm các giá trị trong mẫu: 15 + 17 + 23 + 7 + 9 + 13 = 84 Bây giờ chia kết quả cho số giá trị trong mẫu (trong ví dụ của chúng ta là 6): 84 ÷ 6 = 14. Trung bình mẫu x̅ = 14.
    • Giá trị trung bình của mẫu là giá trị trung tâm mà các giá trị trong mẫu được phân phối. Nếu các giá trị trong cụm mẫu xung quanh mẫu có nghĩa là phương sai nhỏ; nếu không, sự phân tán là lớn.

  4. Trừ giá trị trung bình của mẫu cho mỗi giá trị trong mẫu. Bây giờ hãy tính toán sự khác biệt x i (\ displaystyle x_ (i))- x̅, ở đâu x i (\ displaystyle x_ (i))- mỗi giá trị trong mẫu. Mỗi kết quả cho biết mức độ sai lệch của một giá trị cụ thể so với giá trị trung bình của mẫu, nghĩa là giá trị này cách giá trị trung bình mẫu bao xa.

    • Trong ví dụ của chúng tôi: x 1 (\ displaystyle x_ (1))- x̅ = 17 - 14 = 3 x 2 (\ displaystyle x_ (2))- x̅ = 15 - 14 = 1 x 3 (\ displaystyle x_ (3))- x̅ = 23 - 14 = 9 x 4 (\ displaystyle x_ (4))- x̅ = 7 - 14 = -7 x 5 (\ displaystyle x_ (5))- x̅ = 9 - 14 = -5 x 6 (\ displaystyle x_ (6))- x̅ = 13 - 14 = -1
    • Tính đúng đắn của các kết quả thu được rất dễ xác minh, vì tổng của chúng phải bằng không. Điều này liên quan đến định nghĩa của giá trị trung bình, vì giá trị âm(khoảng cách từ giá trị trung bình đến giá trị nhỏ hơn) được bù đầy đủ giá trị tích cực(khoảng cách từ giá trị trung bình đến giá trị lớn).

  5. Như đã lưu ý ở trên, tổng của sự khác biệt x i (\ displaystyle x_ (i))- x̅ phải bằng không. Nó có nghĩa là phương sai trung bình luôn luôn bằng 0, điều này không đưa ra bất kỳ ý tưởng nào về sự lan truyền các giá trị của một đại lượng nhất định. Để giải quyết vấn đề này, hãy bình phương mỗi điểm khác biệt x i (\ displaystyle x_ (i))- x̅. Điều này sẽ dẫn đến việc bạn chỉ nhận được số dương, mà khi thêm vào sẽ không bao giờ cho 0.

    • Trong ví dụ của chúng tôi: (x 1 (\ displaystyle x_ (1))-x̅) 2 = 3 2 = 9 (\ displaystyle ^ (2) = 3 ^ (2) = 9)(x 2 (\ displaystyle (x_ (2))-x̅) 2 = 1 2 = 1 (\ displaystyle ^ (2) = 1 ^ (2) = 1)9 2 = 81(-7) 2 = 49(-5) 2 = 25(-1) 2 = 1
    • Bạn đã tìm thấy bình phương của sự khác biệt - x̅) 2 (\ displaystyle ^ (2)) cho mỗi giá trị trong mẫu.

  6. Tính tổng các chênh lệch bình phương.Đó là, tìm một phần của công thức được viết như sau: ∑ [( x i (\ displaystyle x_ (i))-x̅) 2 (\ displaystyle ^ (2))]. Ở đây, dấu Σ có nghĩa là tổng bình phương của sự khác biệt cho mỗi giá trị x i (\ displaystyle x_ (i)) trong mẫu. Bạn đã tìm thấy sự khác biệt bình phương (x i (\ displaystyle (x_ (i))-x̅) 2 (\ displaystyle ^ (2)) cho mỗi giá trị x i (\ displaystyle x_ (i)) trong mẫu; bây giờ chỉ cần thêm những hình vuông này.

    • Trong ví dụ của chúng tôi: 9 + 1 + 81 + 49 + 25 + 1 = 166 .

  7. Chia kết quả cho n - 1, với n là số giá trị trong mẫu. Cách đây một thời gian, để tính phương sai mẫu, các nhà thống kê chỉ cần chia kết quả cho n; trong trường hợp này, bạn sẽ nhận được giá trị trung bình của phương sai bình phương, lý tưởng để mô tả phương sai của một mẫu nhất định. Nhưng hãy nhớ rằng bất kỳ mẫu nào cũng chỉ là một phần nhỏ. dân số các giá trị. Nếu bạn lấy một mẫu khác và thực hiện các phép tính tương tự, bạn sẽ nhận được một kết quả khác. Hóa ra, phép chia cho n - 1 (và không chỉ n) cho nhiều hơn ước tính chính xác phương sai dân số, đó là điều bạn quan tâm. Chia cho n - 1 đã trở nên phổ biến, vì vậy nó được đưa vào công thức tính phương sai mẫu.

    • Trong ví dụ của chúng tôi, mẫu bao gồm 6 giá trị, tức là, n = 6. Phương sai mẫu = s 2 = 166 6 - 1 = (\ displaystyle s ^ (2) = (\ frac (166) (6-1)) =) 33,2

  8. Sự khác biệt giữa phương sai và độ lệch chuẩn. Lưu ý rằng công thức có chứa số mũ, vì vậy phương sai được đo bằng đơn vị bình phương của giá trị được phân tích. Đôi khi một giá trị như vậy khá khó hoạt động; trong những trường hợp như vậy, hãy sử dụng độ lệch chuẩn, bằng căn bậc hai khỏi phân tán. Đó là lý do tại sao phương sai mẫu được biểu thị là s 2 (\ displaystyle s ^ (2)), một độ lệch chuẩn mẫu - làm thế nào s (\ displaystyle s).

    • Trong ví dụ của chúng tôi, độ lệch chuẩn mẫu là: s = √33,2 = 5,76.

    Tính toán phương sai tổng thể

    1. Phân tích một số bộ giá trị. Tập hợp bao gồm tất cả các giá trị của đại lượng đang được xem xét. Ví dụ: nếu bạn nghiên cứu tuổi của cư dân Vùng Leningrad, thì dân số bao gồm tuổi của tất cả cư dân của khu vực này. Trong trường hợp làm việc với tổng hợp, bạn nên tạo một bảng và nhập các giá trị của tổng hợp vào đó. Hãy xem xét ví dụ sau:

      • Có 6 bể cá trong một phòng nhất định. Mỗi bể chứa số lượng cá sau: x 1 = 5 (\ displaystyle x_ (1) = 5)x 2 = 5 (\ displaystyle x_ (2) = 5)x 3 = 8 (\ displaystyle x_ (3) = 8)x 4 = 12 (\ displaystyle x_ (4) = 12)x 5 = 15 (\ displaystyle x_ (5) = 15)x 6 = 18 (\ displaystyle x_ (6) = 18)

    2. Viết công thức tính phương sai tổng thể. Vì tổng thể bao gồm tất cả các giá trị của một số lượng nhất định, công thức sau đây cho phép bạn nhận được giá trị chính xác của phương sai của tổng thể. Để phân biệt phương sai tổng thể với phương sai mẫu (chỉ là ước tính), các nhà thống kê sử dụng các biến khác nhau:

      • σ 2 (\ displaystyle ^ (2)) = (∑(x i (\ displaystyle x_ (i)) - μ) 2 (\ displaystyle ^ (2))) / N
      • σ 2 (\ displaystyle ^ (2))- phương sai tổng thể (đọc là "bình phương sigma"). Độ phân tán được đo bằng đơn vị bình phương.
      • x i (\ displaystyle x_ (i))- mỗi giá trị trong tổng thể.
      • Σ là dấu của tổng. Đó là, đối với mỗi giá trị x i (\ displaystyle x_ (i)) trừ đi μ, bình phương nó, và sau đó cộng các kết quả.
      • μ là giá trị trung bình của quần thể.
      • n là số giá trị trong tổng thể chung.

    3. Tính trung bình dân số. Khi làm việc với dân số chung, giá trị trung bình của nó được ký hiệu là μ (mu). Giá trị trung bình của tổng thể được tính như giá trị trung bình thông thường: cộng tất cả các giá trị trong tổng thể, sau đó chia kết quả cho số giá trị trong tổng thể.

      • Hãy nhớ rằng giá trị trung bình không phải lúc nào cũng được tính là giá trị trung bình cộng.
      • Trong ví dụ của chúng tôi, dân số có nghĩa là: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\ displaystyle (\ frac (5 + 5 + 8 + 12 + 15 + 18) (6))) = 10,5

    4. Trừ trung bình dân số cho mỗi giá trị trong tổng thể. Giá trị chênh lệch càng gần bằng 0, thì giá trị cụ thể càng gần với giá trị trung bình của tổng thể. Tìm sự khác biệt giữa mỗi giá trị trong tổng thể và giá trị trung bình của nó, và bạn sẽ có cái nhìn đầu tiên về sự phân bố của các giá trị.

      • Trong ví dụ của chúng tôi: x 1 (\ displaystyle x_ (1))- μ = 5 - 10,5 = -5,5 x 2 (\ displaystyle x_ (2))- μ = 5 - 10,5 = -5,5 x 3 (\ displaystyle x_ (3))- μ = 8 - 10,5 = -2,5 x 4 (\ displaystyle x_ (4))- μ = 12 - 10,5 = 1,5 x 5 (\ displaystyle x_ (5))- μ = 15 - 10,5 = 4,5 x 6 (\ displaystyle x_ (6))- μ = 18 - 10,5 = 7,5

    5. Bình phương mỗi kết quả bạn nhận được. Các giá trị chênh lệch sẽ là cả dương và âm; nếu bạn đặt các giá trị này trên một dòng số, thì chúng sẽ nằm ở bên phải và bên trái của trung bình dân số. Điều này không phù hợp để tính toán phương sai, vì dương và số âm bù trừ lẫn nhau. Do đó, hãy bình phương mỗi chênh lệch để nhận được các số dương duy nhất.

      • Trong ví dụ của chúng tôi: (x i (\ displaystyle x_ (i)) - μ) 2 (\ displaystyle ^ (2)) cho mỗi giá trị dân số (từ i = 1 đến i = 6): (-5,5)2 (\ displaystyle ^ (2)) = 30,25(-5,5)2 (\ displaystyle ^ (2)), ở đâu x n (\ displaystyle x_ (n)) – giá trị cuối cùng trong dân số nói chung.
      • Để tính giá trị trung bình của các kết quả thu được, bạn cần tìm tổng của chúng và chia nó cho n: (( x 1 (\ displaystyle x_ (1)) - μ) 2 (\ displaystyle ^ (2)) + (x 2 (\ displaystyle x_ (2)) - μ) 2 (\ displaystyle ^ (2)) + ... + (x n (\ displaystyle x_ (n)) - μ) 2 (\ displaystyle ^ (2))) / N
      • Bây giờ chúng ta hãy viết lời giải thích ở trên bằng cách sử dụng các biến: (∑ ( x i (\ displaystyle x_ (i)) - μ) 2 (\ displaystyle ^ (2))) / n và nhận công thức tính phương sai tổng thể.

Từ khóa » Tính Kỳ Vọng Và Phương Sai Trong Excel