Công Thức Tính Diện Tích Hình Tam Giác, Chu Vi Hình Tam Giác
Có thể bạn quan tâm
Công thức tính diện tích hình tam giác, chu vi hình tam giác bao gồm công thức tính diện tích tam giác thường, tam giác vuông, tam giác cân, tam giác đều và chu vi hình tam giác được trình bày chi tiết.
Diện tích hình tam giác
- 1. Công thức tính diện tích tam giác thường
- 2. Công thức tính diện tích tam giác vuông
- 3. Công thức tính diện tích tam giác cân
- 4. Công thức tính diện tích tam giác đều
- 5. Công thức tính chu vi tam giác
- 6. Bài tập về hình tam giác
1. Công thức tính diện tích tam giác thường
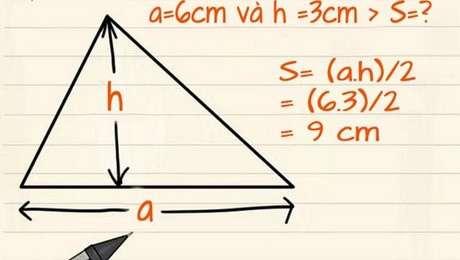
+ Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2. Nói cách khác, diện tích tam giác thường sẽ bằng 1/2 tích của chiều cao và chiều dài cạnh đáy của tam giác.
+ Đơn vị: cm2, m2, dm2, ….
Công thức tính diện tích tam giác thường:
![]() \(S=\frac{a\times h}{2}\)
\(S=\frac{a\times h}{2}\)
Trong đó:
+ a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)
+ h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác)
Công thức suy ra:
![]() \(h=\frac{S\times2}{a}\ hoặc\ a=\frac{S\times2}{h}\)
\(h=\frac{S\times2}{a}\ hoặc\ a=\frac{S\times2}{h}\)
* Chú ý: Trường hợp không cho cạnh đáy hoặc chiều cao, mà cho trước diện tích và cạnh còn lại, các bạn hãy áp dụng công thức suy ra ở trên để tính toán.
2. Công thức tính diện tích tam giác vuông
- Diễn giải: Công thức tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường (hình tam giác vuông sẽ khác biệt hơn so với tam giác thường do thể hiện rõ chiều cao và chiều dài cạnh đáy, và bạn không cần vẽ thêm để tính chiều cao tam giác).
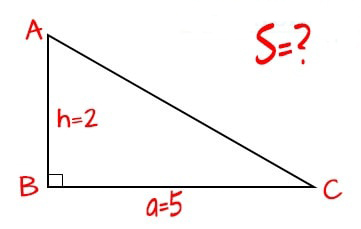
Công thức tính diện tích tam giác vuông:
![]() \(S=\frac{a\times b}{2}\)
\(S=\frac{a\times b}{2}\)
Trong đó a, b: độ dài hai cạnh góc vuông
Công thức suy ra:
a = (S x 2) : b hoặc b = (S x 2) : a
3. Công thức tính diện tích tam giác cân
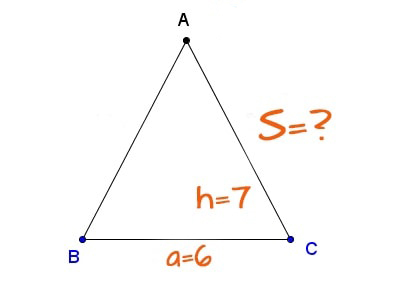
Công thức tính diện tích tam giác cân:
![]() \(S=\frac{a\times h}{2}\)
\(S=\frac{a\times h}{2}\)
+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Bài tập ví dụ
* Tính diện tích của tam giác cân có:
a, Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm
b, Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m
4. Công thức tính diện tích tam giác đều
Diễn giải:
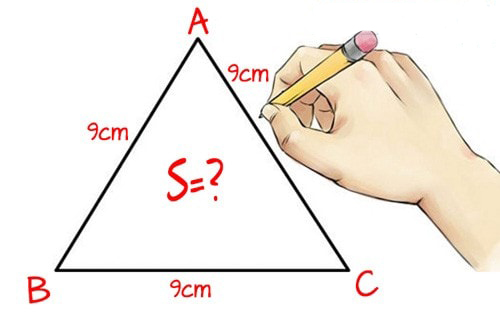
Tam giác đều là tam giác có 3 cạnh bằng nhau. Trong đó cách tính diện tích tam giác đều cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
+ Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.
Công thức tính diện tích tam giác đều:
![]() \(S=\frac{a\times h}{2}\)
\(S=\frac{a\times h}{2}\)
+ a: Chiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
5. Công thức tính chu vi tam giác
Công thức, cách tính chu vi tam giác
Chu vi tam giác: C = a + b + c
Trong đó a, b, c lần lượt là chiều dài 3 cạnh của tam giác.
>> Tham khảo chi tiết: Công thức tính chu vi tam giác.
6. Bài tập về hình tam giác
Mời bạn đọc Tải về Bài tập về hình tam giác để xem đầy đủ nội dung chi tiết bài tập và hướng dẫn giải bài tập
Từ khóa » Cách Tính Diện Tích Tam Giác
-
Công Thức Tính Diện Tích Tam Giác: Vuông, Thường, Cân, đều
-
Công Thức Tính Diện Tích Tam Giác 2022
-
Công Thức Tính Diện Tích Tam Giác: đều, Cân, Vuông, Thường Từ A - Z
-
Công Thức Tính Diện Tích Tam Giác: Thường, Cân, Vuông, đều & Các ...
-
Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, đều, Bài Tập Có
-
Tam Giác? Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, đều
-
Công Thức Tính Diện Tích Tam Giác - Gia Sư Tâm Tài Đức
-
Cách Tính Diện Tích Tam Giác Thường, Vuông, Cân Và Tam Giác đều
-
Tổng Hợp Các Công Thức Tính Diện Tích Tam Giác Chi Tiết Nhất
-
Công Thức Tính Diện Tích Tam Giác - Mobitool
-
Công Thức Tính Diện Tích Tam Giác Vuông - Mobitool
-
Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, Đều
-
8 Công Thức Tính Diện Tích Tam Giác - Toán Học Việt Nam
-
Công Thức Cách Tính Diện Tích Hình Tam Giác Thường, đều, Vuông, Cân