Công Thức Tính Diện Tích Tam Giác 2022
Có thể bạn quan tâm
Hình tam giác là hình thường gặp trong quá trình học Toán đối với các em học sinh. Hoatieu.vn sẽ giới thiệu đến các bạn những cách tính diện tích tam giác dễ hiểu và được sử dụng phổ biến nhất.
Bài viết dưới đây Hoatieu.vn sẽ cung cấp cho các em học sinh kiến thức về cách tính, côn thức tính diện tích hình tam giác đều, vuông, cân, tam giác thường một cách nhanh chóng, chính xác nhất.
Hướng dẫn tính diện tích hình tam giác
- 1. Công thức tính diện tích tam giác thường, vuông, cân, đều, nâng cao.
- 1.1. Công thức tính diện tích tam giác thường
- 1.2. Công thức tính diện tích tam giác vuông
- 1.3. Công thức tính diện tích tam giác cân
- 1.4. Công thức tính diện tích tam giác đều
- 1.5. Công thức tính diện tích tam giác nâng cao
- 2. Công thức tính chu vi hình tam giác
- 2.1. Tính chu vi tam giác thường
- 2.2. Công thức tính chu vi tam giác cân
- 2.3. Cách tính chu vi tam giác đều
- 2.4. Chu vi tam giác vuông
- 3. Hình tam giác là gì?
- 4. Các loại hình tam giác
- 5. Các dạng bài tập tính diện tích tam giác cơ bản và nâng cao
- Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao
- Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao
- Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy
1. Công thức tính diện tích tam giác thường, vuông, cân, đều, nâng cao.
1.1. Công thức tính diện tích tam giác thường
Diễn giải:
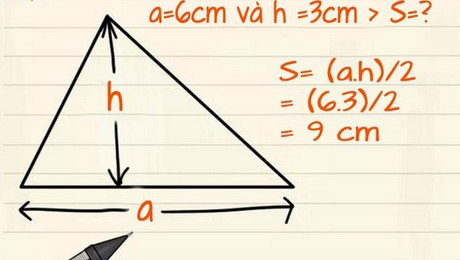
+ Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2. Nói cách khác, diện tích tam giác thường sẽ bằng 1/2 tích của chiều cao và chiều dài cạnh đáy của tam giác.
+ Đơn vị: cm2, m2, dm2, ….
Công thức tính diện tích tam giác thường:
S = (a x h) / 2
Trong đó:
+ a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)
+ h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác)
Công thức suy ra:
h = (S x 2) / a hoặc a = (S x 2) / h
Bài tập ví dụ
* Tính diện tích hình tam giác có
a, Độ dài đáy là 15cm và chiều cao là 12cm
b, Độ dài đáy là 6m và chiều cao là 4,5m
Lời giải:
a, Diện tích của hình tam giác là:
(15 x 12) : 2 = 90 (cm2)
Đáp số: 90cm2
b, Diện tích của hình tam giác là:
(6 x 4,5) : 2 = 13,5 (m2)
Đáp số: 13,5m2
* Chú ý: Trường hợp không cho cạnh đáy hoặc chiều cao, mà cho trước diện tích và cạnh còn lại, các bạn hãy áp dụng công thức suy ra ở trên để tính toán.
1.2. Công thức tính diện tích tam giác vuông
- Diễn giải: Công thức tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường, đó là bằng1/2 tích của chiều cao với chiều dài đáy. Mặc dù vậy hình tam giác vuông sẽ khác biệt hơn so với tam giác thường do thể hiện rõ chiều cao và chiều dài cạnh đáy, và bạn không cần vẽ thêm để tính chiều cao tam giác.
Công thức tính diện tích tam giác vuông: S = (A X H) / 2
Diễn giải:
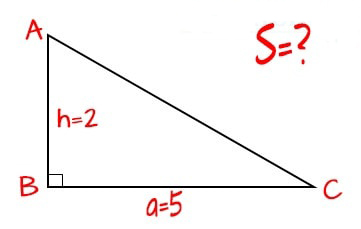
+ Công thức tính diện tích tam giác vuông tương tự với cách tính diện tích tam giác thường, đó là bằng1/2 tích của chiều cao với chiều dài đáy. Vì tam giác vuông là tam giác có hai cạnh góc vuông nên chiều cao của tam giác sẽ ứng với một cạnh góc vuông và chiều dài đáy ứng với cạnh góc vuông còn lại
Công thức tính diện tích tam giác vuông:
S = (a x b)/ 2
Trong đó a, b: độ dài hai cạnh góc vuông
Công thức suy ra:
a = (S x 2) : b hoặc b = (S x 2) : a
Bài tập ví dụ
* Tính diện tích của tam giác vuông có:
a, Hai cạnh góc vuông lần lượt là 3cm và 4cm
b, Hai cạnh góc vuông lần lượt là 6m và 8m
Lời giải:
a, Diện tích của hình tam giác là:
(3 x 4) : 2 = 6 (cm2)
Đáp số: 6cm2
b, Diện tích của hình tam giác là:
(6 x 8) : 2 = 24 (m2)
Đáp số: 24m2
Tương tự nếu dữ liệu hỏi ngược về cách tính độ dài, các bạn có thể sử dụng công thức suy ra ở trên.
1.3. Công thức tính diện tích tam giác cân
Diễn giải:
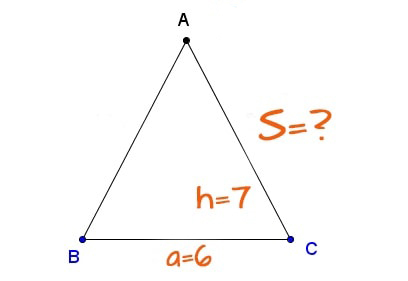
Tam giác cân là tam giác trong đó có hai cạnh bên và hai góc bằng nhau. Trong đó cách tính diện tích tam giác cân cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
+ Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.
Công thức tính diện tích tam giác cân:
S = (a x h)/ 2
+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Bài tập ví dụ
* Tính diện tích của tam giác cân có:
a, Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm
b, Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m
Lời giải:
a, Diện tích của hình tam giác là:
(6 x 7) : 2 = 21 (cm2)
Đáp số: 21cm2
b, Diện tích của hình tam giác là:
(5 x 3,2) : 2 = 8 (m2)
Đáp số: 8m2
1.4. Công thức tính diện tích tam giác đều
Diễn giải:
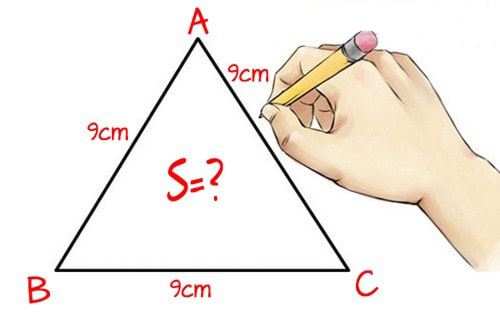
Tam giác đều là tam giác có 3 cạnh bằng nhau. Trong đó cách tính diện tích tam giác đều cũng tương tự cách tính tam giác thường, chỉ cần bạn biết chiều cao tam giác và cạnh đáy.
+ Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.
Công thức tính diện tích tam giác đều:
S = (a x h)/ 2
+ a: Chiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Bài tập ví dụ
* Tính diện tích của tam giác đều có:
a, Độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm
b, Độ dài một cạnh tam giác bằng 4cm và đường cao bằng 5cm
Lời giải
a, Diện tích hình tam giác là:
(6 x 10) : 2 = 30 (cm2)
Đáp số: 30cm2
b, Diện tích hình tam giác là:
(4 x 5) : 2 = 10 (cm2)
Đáp số: 10cm2
Dù sử dụng công thức tính diện tích tam giác nào đi chăng nữa thì các bạn, các em học sinh, sinh viên cần hiểu rằng, không phải lúc chiều cao cũng nằm trong tam giác, lúc này cần vẽ thêm một chiều cao và cạnh đáy bổ sung. Và quan trọng khi tính diện tích tam giác, cần chú ý chiều cao phải ứng với cạnh đáy nơi nó chiếu xuống.
1.5. Công thức tính diện tích tam giác nâng cao
Ngoài những cách tính diện tích tam giác ở trên, thực tế, toán học còn phổ biến các cách tính diện tích tam giác bằng công thức Heron, tính diện tích tam giác bằng góc và hàm lượng giác. Cụ thể:
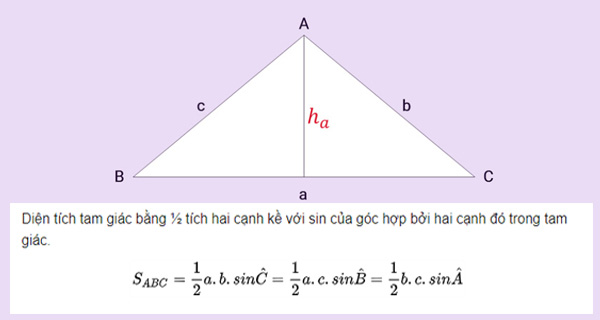
* Công thức diện tích tam giác khi biết 1 góc
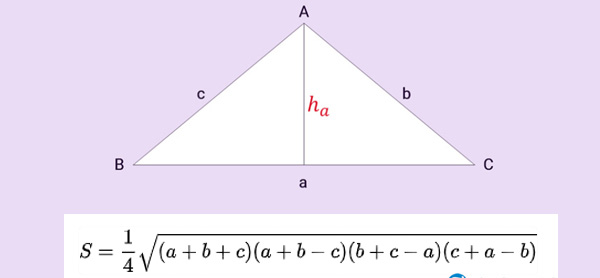
* Công thức tính diện tích tam giác theo công thức Heron
* Cách tính diện tích tam giác mở rộng
Lưu ý: Khi dùng công thức này thì bạn cần chứng minh trước.
Công thức 1:
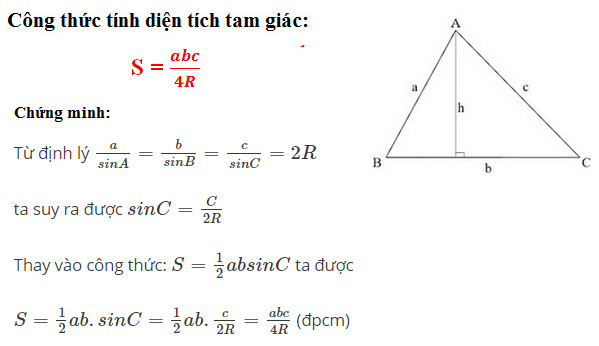
Trong đó:
- a, b, c: Độ dài cạnh của tam giác- R: Bán kính đường tròn ngoại tiếp tam giác
Công thức 2:
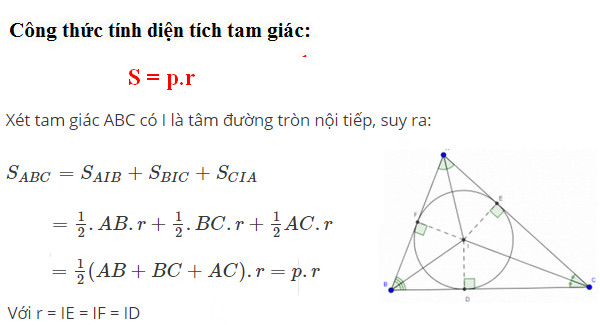
Trong đó:
- p: nửa chu vi tam giác- r: bán kính đường tròn nội tiếp tam giác
Ngoài ra, bài viết còn bổ sung kiến thức về công thức tính chu vi tam giác và các dạng bài tập tính diện tích tam giác cơ bản và nâng cao giúp em học sinh, sinh viên tham khảo để áp dụng, luyện tập giải bài tập tính diện tích tam giác một cách nhanh chóng và dễ dàng.
2. Công thức tính chu vi hình tam giác
2.1. Tính chu vi tam giác thường
Tam giác thường là tam giác cơ bản có 3 cạnh với độ dài khác nhau. Công thức tính chu vi hình tam giác thường:
P = a + b + c
Trong đó:
- P là chu vi tam giác.
- a, b, c là 3 cạnh của hình tam giác đó.
Để tính diện tích nửa chu vi tam giác sẽ dựa theo công thức: ½P = (a+b+c) : 2
Ví dụ: Cho tam giác có độ dài 3 cạnh lần lượt là 4cm, 8cm và 9cm. Tính chu vi hình tam giác.
Dựa vào công thức chúng ta sẽ có lời giải là P = 4 + 8 + 9 = 21cm
2.2. Công thức tính chu vi tam giác cân
Tam giác cân là tam giác có 2 cạnh và 2 góc bằng nhau. Đỉnh của tam giác cân là giao diện của 2 cạnh bên.
Để tính chu vi tam giác cân, bạn cần biết đỉnh của tam giác cân và độ dài 2 cạnh là được. Công thức tính chu vi hình tam giác cân là:
P = 2a + c
Trong đó:
- a: Hai cạnh bên của tam giác cân.
- c: Là đáy của tam giác.
Lưu ý, công thức tính chu vi tam giác cân sẽ được áp dụng để tính chu vi của tam giác vuông cân.
Ví dụ: Cho hình tam giác cân tại A với chiều dài AB = 7cm, BC = 5cm. Tính chu vi hình tam giác cân.
Dựa vào công thức tính chu vi tam giác cân, ta có cách tính P = 7 + 7 + 5 = 19cm.
2.3. Cách tính chu vi tam giác đều
Tam giác đều là trường hợp đặc biệt của tam giác cân khi 3 cạnh bằng nhau. Công thức tính tam giác đều là:
P = 3 x a
Trong đó
- P: Là chu vi tam giác đều.
- a: Là chiều dài cạnh của tam giác.
Ví dụ: Tính chu vi tam giác đều có cạnh AB = 5cm.
Dựa theo công thức chúng ta có cách tính P = 5 x 3 = 15cm.
2.4. Chu vi tam giác vuông
Tam giác vuông là tam giác có 1 góc vuông 90°. Công thức tính chu vi tam giác vuông là:
P = a + b + c
Trong đó
- a và b: Hai cạnh của tam giác vuông.
- c: Cạnh huyền của tam giác vuông.
Ví dụ: Tính chu vi tam giác vuông với độ dài CA = 6cm, CB = 7cm và AB = 10cm.
Dựa vào công thức tính chúng ta có cách tính P = 6 + 7 + 10 = 23cm.
Ngoài ra chúng ta cũng có thể tính chu vi của tam giác vuông khi biết độ dài 2 cạnh. Cho tam giác vuông với chiều dài CA = 5cm, CB = 8cm, tính chu vi.
Như hình dưới đây do tam giác vuông ở C nên cạnh huyền là AB. Để tính cạnh huyền tam giác vuông cân, ta sẽ dựa theo định lý Pitago trong tam giác vuông.
AB² = CA² + CB²
AB² = 25 + 64
AB = 9,4cm
Vậy chu vi tam giác vuông CAB là:
P = 5 + 8 + 9,4 = 22,4cm
3. Hình tam giác là gì?
Tam giác hay hình tam giác là một loại hình cơ bản trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là đa giác có số cạnh ít nhất (3 cạnh). Tam giác luôn luôn là một đa giác đơn và luôn là một đa giác lồi (các góc trong luôn nhỏ hơn 180o).
Công thức tính diện tích tam giác là một kiến thức quan trọng xuyên suốt theo các bạn học sinh từ lớp 5 đến lớp 12 và cả ra ngoài đời sống, áp dụng vào công việc.
4. Các loại hình tam giác
Tam giác thường: là tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau. Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt của tam giác.
Tam giác cân: là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy. Tính chất của tam giác cân là hai góc ở đáy thì bằng nhau.
Tam giác đều: là trường hợp đặc biệt của tam giác cân có cả ba cạnh bằng nhau. Tính chất của tam giác đều là có 3 góc bằng nhau và bằng 60 độ.
5. Các dạng bài tập tính diện tích tam giác cơ bản và nâng cao
Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao
Ví dụ 1: Tính diện tích tam giác thường và tam giác vuông có:
a) Độ dài đáy bằng 32cm và chiều cao bằng 25cm.
b) Hai cạnh góc vuông có độ dài lần lượt là 3dm và 4dm.
Bài làm
a) Diện tích hình tam giác là:
32 x 25 : 2 = 400 (cm2)
b) Diện tích hình tam giác là:
3 x 4 : 2 = 6 (dm2)
Đáp số: a) 400cm2
b) 6dm2
Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao
+ Từ công thức tính diện tích, ta suy ra công thức tính độ dài đáy: a = S x 2 : h
Ví dụ 1: Tính độ dài cạnh đáy của hình tam giác có chiều cao bằng 80cm và diện tích bằng 4800cm2.
Bài làm
Độ dài cạnh đáy của hình tam giác là:
4800 x 2 : 80 = 120 (cm)
Đáp số: 120cm
Ví dụ 2: Cho hình tam giác có diện tích 5/8m2 chiều cao là 1/2 m. Tính độ dài cạnh đáy của tam giác đó?
Bài làm
Độ dài cạnh đáy của tam giác là:
![]() \(\frac{5}{8} \times 2:\frac{1}{2} = \frac{{20}}{8} = \frac{5}{2}\)(m)
\(\frac{5}{8} \times 2:\frac{1}{2} = \frac{{20}}{8} = \frac{5}{2}\)(m)
Đáp số: 5/2m
Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy
+ Từ công thức tính diện tích, ta suy ra công thức tính chiều cao: h = S x 2 : a
Ví dụ 1: Tính chiều cao của hình tam giác có độ dài cạnh đáy bằng 50cm và diện tích bằng 1125cm2.
Bài làm
Chiều cao của hình tam giác là:
1125 x 2 : 50 = 45 (cm)
Đáp số: 45cm
Bài viết trên đây Hoatieu.vn đã trình bày Cách tính diện tích tam giác: vuông, thường, cân, đều và các dạng bài tập cơ bản, nâng cao giúp bạn đọc tính S tam giác nhanh chóng, hiệu quả nhất được chúng tôi sưu tầm từ các nguồn. Thực tế là có rất nhiều cách tính S tam giác, tuy nhiên, để thực hiện tính S tam giác chính xác và nhanh chóng, các bạn cần thường xuyên luyện tập để vận dụng công thức tính cho phù hợp nhất.
Hy vọng nội dung bài viết đã cung cấp những thông tin hữu ích đến cho bạn đọc. Nếu có bất kì thắc mắc nào, hãy liên hệ với HoaTieu.vn hoặc để lại câu hỏi tại phần bình luận, chúng tôi sẽ giải đáp sớm nhất có thể.
Mời các bạn tham khảo thêm các thông tin hữu ích khác trên chuyên mục Tài liệu của HoaTieu.vn.
Từ khóa » Tính Diện Tích Của Hình Tam Giác đó
-
Công Thức Tính Diện Tích Tam Giác: đều, Cân, Vuông, Thường Từ A - Z
-
Công Thức Tính Diện Tích Tam Giác: Vuông, Thường, Cân, đều
-
Công Thức Tính Diện Tích Tam Giác
-
Công Thức Tính Diện Tích Tam Giác: Thường, Cân, Vuông, đều & Các ...
-
Công Thức Tính Diện Tích Hình Tam Giác, Chu Vi Hình Tam Giác
-
Công Thức Tính Diện Tích Hình Tam Giác - LabVIETCHEM
-
Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, đều, Bài Tập Có
-
Tam Giác? Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, đều
-
Công Thức Cách Tính Diện Tích Hình Tam Giác Thường, đều, Vuông, Cân
-
Hướng Dẫn Cách Tính Diện Tích Hình Tam Giác Lớp 5 - ReviewEdu
-
[ Công Thức Tính Diện Tích Hình Tam Giác ] Tam Giác Thường, Vuông ...
-
Lý Thuyết Diện Tích Hình Tam Giác | SGK Toán Lớp 5
-
Lý Thuyết Tam Giác. Diện Tích Hình Tam Giác Toán 5
-
Cách Tính Diện Tích Hình Tam Giác (Vuông / Cân / Đều / Thường)