Công Thức Tính Diện Tích Tam Giác, Bán Kính đường Tròn Ngoại Tiếp ...

Trang chủ » Công Thức đường Tròn Ngoại Tiếp » Công Thức Tính Diện Tích Tam Giác, Bán Kính đường Tròn Ngoại Tiếp ...

Có thể bạn quan tâm

Cách tính diện tích tam giác, bán kính đường tròn ngoại tiếp tam giác, nội tiếp tam giác .

Cho tam giác ABC. Gọi a, b, c lần lượt là độ dài các cạnh BC, AC, AB

Nửa chu vi tam giác là:

Ta có các hệ thức cơ bản:

  • Công thức tính diện tích tam giác là: (áp dụng công thức herong)

  • Công thức tính bán kính đường tròn nội tiếp tam giác là:

  • Công thức tính bán kính đường tròn ngoại tiếp tam giác bằng:

-Công thức tính bán kính đường tròn ngoại tiếp góc A:

-Công thức tính bán kính đường tròn ngoại tiếp góc B:

-Công thức tính bán kính đường tròn ngoại tiếp góc C:

Ví dụ:

Tam giác  ABC  có cạnh  AB=3 cm, AC=7cm, BC=8cm.

  1. Tính diện tích của tam giác.
  2. Tính bán kính các đường tròn nội tiếp, ngoại tiếp của tam giác.
  • Nửa chu vi tam giác là:

  • Diện tích của tam giác bằng:

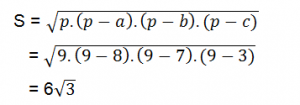
  • Bán kính đường tròn nội tiếp tam giác bằng:

  • Bán kính đường tròn ngoại tiếp tam giác bằng:

Trên đây là công thức và bài tập ví dụ về công thức tính diện tích tam giác, bán kính đường tròn ngoại tiếp tam giác, nội tiếp tam giác. Các bạn cùng tham khảo nhé.

Chúc các bạn học tốt!

Từ khóa » Công Thức đường Tròn Ngoại Tiếp