Công Thức Tính Diện Tích Tam Giác Thường, Cân, Vuông, đều Chuẩn ...
Có thể bạn quan tâm
Bạn gặp bài toán tính diện tích của một mảnh đất hình tam giác nhưng bạn không biết cách tính như thế nào? Sau đây, điện máy Ebest sẽ chia sẻ công thức tính diện tích tam giác thường, cân, vuông và đều kèm theo các bài tập minh họa có lời giải để các bạn cùng tham khảo
Công thức tính diện tích tam giác
Nội dung bài viết
- Công thức tính diện tích tam giác
- Tính diện tích tam giác khi biết một góc
- Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron
- Tính diện tích tam giác theo bán kính đường tròn ngoại tiếp
- Công thức tính diện tích tam giác cân
- Công thức tính diện tích tam giác đều
- Công thức tính diện tích tam giác vuông
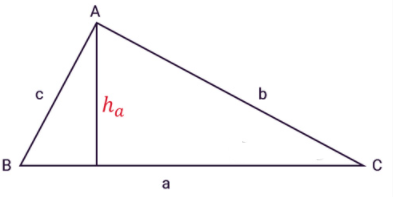
Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2. Nói cách khác dễ hiểu hơn, diện tích tam giác thường bằng ½ tích của chiều cao hạ từ đỉnh và chiều dài cạnh đáy đối diện của đỉnh tam giác đó
S = ½.a.h
Trong đó:
- a: Chiều dài cạnh đáy tam giác.
- h: Chiều cao được nối từ đỉnh và vuông góc với đáy của tam giác.
Ví dụ: Tính diện tích hình tam giác có độ dài đáy là 6m và chiều cao là 25dm.
Lời giải:
Chiều cao 25dm = 2,5m
Diện tích tam giác là
S = ½.a.h = ½.6.2,5 = 7,5 m2
Tính diện tích tam giác khi biết một góc
Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
S = ½a.bsinC∧ = ½a.c.sinB∧ = ½b.c.sinA∧
Ví dụ: Tam giác ABC có cạnh BC = 8, cạnh AB = 5, góc B bằng 60 độ. Tính diện tích tam giác ABC?
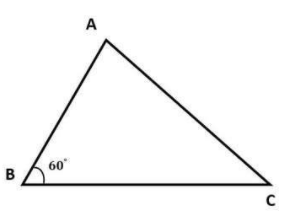
Giải:
Áp dụng công thức tính diện tích ta có:
S = ½a.c.sinB∧ = ½.8.5.sin600 = 40√3/4 m2
Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron
Áp dụng công thức Heron, ta có công thức tính diện tích tam giác là:
S = √p(p – a)(p – b)(p – c) = 1/4√(a + b + c)(a + b – c)(b + c – a)(c + a – b)
Trong đó:
- a, b, c: Lần lượt là các cạnh của tam giác.
- p: Nửa chu vi của tam giác, có công thức là: p = (a + b + c) / 2
Ví dụ: Tính diện tích hình tam giác có độ dài cạnh AB = 8, AC = 7, CB = 9
Lời giải
Nửa chu vi của tam giác ABC là:
p = (AB + AC + BC)/2 = (8 + 7 + 9) : 2 = 12
Áp dụng công thức Heron, ta có diện tích của tam giác ABC là:
S = √p(p – a)(p – b)(p – c) = √12(12 – 8)(12 – 7)(12 – 9) = 12√5
Tính diện tích tam giác theo bán kính đường tròn ngoại tiếp
SABC = abc/4R
Hoặc SABC = 2R2 x sinA∧ x sinB∧ x sinC∧
Trong đó:
- a, b, c: Lần lượt là các cạnh của tam giác.
- R: Bán kính đường tròn ngoại tiếp tam giác.
- A, B, C: Lần lượt là các góc tại đỉnh A, B, C.
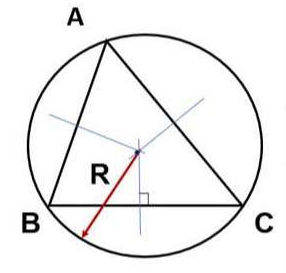
Ví dụ: Cho tam giác ABC, độ dài các cạnh lần lượt là: a = 6, b = 7, c = 5, R = 3 (với R là bán kính đường tròn ngoại tiếp tam giác ABC).
Hướng dẫn:
Áp dụng công thức, ta có:
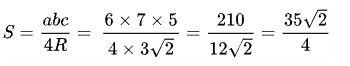
Tham khảo thêm:
- Diện tích hình tròn, chu vi hình tròn đầy đủ [Có ví dụ minh họa]
- Công thức tính diện tích hình thang: thường, vuông, cân chính xác 100%
- Công thức tính diện tích hình bình hành, chu vi hình bình hành từ A – Z
Công thức tính diện tích tam giác cân
Diện tích tam giác cân bằng ½ tích của chiều cao với độ dài cạnh đáy.
S = ½.a.h
Trong đó:
- a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
- h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Ví dụ: Cho tam giác ABC cân tại A, có đường cao bằng 6 cm và độ dài cạnh đáy bằng 5 cm. Tính diện tích tam giác cân ABC?
Hướng dẫn:
Gọi h là đường cao của tam giác cân ABC, a là độ dài cạnh đáy.
Áp dụng công thức, ta có diện tích tam giác cân ABC là:
S = ½.a.h = ½. 6.5 = 15 (cm²)
Công thức tính diện tích tam giác đều
Diện tích tam giác đều cũng tương tự như cách tính diện tích tam giác thường bằng 1/2 tích của đường cao nối từ đỉnh nhân với cạnh đáy của tam giác đó.
S = ½.a.h
Trong đó:
- a: Chiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
- h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).
Ví dụ: Tính diện tích tam giác đều biết độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm
Lời giải:
Áp dụng công thức trên ta có:
S = ½.a.h = ½.6.10 = 30 cm2
Công thức tính diện tích tam giác vuông
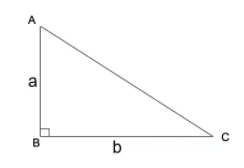
Diện tích tam giác vuông bằng 1/2 tích của chiều cao với độ dài cạnh đáy.
S = ½.a.b
Trong đó:
- b là cạnh đáy của tam giác.
- a là chiều cao của tam giác
Ví dụ: Tính diện tích của tam giác vuông biết hai cạnh góc vuông lần lượt là 3cm và 4cm
Lời giải
Áp dụng công thức trên ta có:
S = ½.a.b = ½.3.4 = 6cm2
Hy vọng với những kiến thức mà chúng tôi vừa chia sẻ có thể giúp các bạn nắm được các công thức tính diện tích tam giác thường, vuông, cân và đều để vận dụng vào làm bài tập đơn giản hơn nhé
Đánh giá bài viếtTừ khóa » Cách Tính Diện Tích Tam Giác Thường
-
Công Thức Tính Diện Tích Tam Giác: Vuông, Thường, Cân, đều
-
Công Thức Tính Diện Tích Tam Giác 2022
-
Công Thức Tính Diện Tích Tam Giác: Thường, Cân, Vuông, đều & Các ...
-
Công Thức Tính Diện Tích Tam Giác: đều, Cân, Vuông, Thường Từ A - Z
-
Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, đều, Bài Tập Có
-
Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, Đều
-
Công Thức Cách Tính Diện Tích Hình Tam Giác Thường, đều, Vuông, Cân
-
Cách Tính Diện Tích Tam Giác Thường, Vuông, Cân Và Tam Giác đều
-
Công Thức Tính Diện Tích Tam Giác Thường , Vuông , Cân, đều....
-
Tam Giác? Công Thức Tính Diện Tích Tam Giác Thường, Vuông, Cân, đều
-
Công Thức Tính Diện Tích Tam Giác Vuông - Mobitool
-
1. Công Thức Tính Diện Tích Tam Giác
-
Công Thức Tính Diện Tích Tam Giác: Thường, Vuông, Cân, Đều
-
Công Thức Tính Diện Tích Hình Tam Giác - LabVIETCHEM