Công Thức Tính Diện Tích Xung Quanh Hình Trụ
Có thể bạn quan tâm
Chủ đề diện tích xq hình trụ: Diện tích xq hình trụ là một tính chất quan trọng của hình trụ, cho phép ta tính được phần diện tích bao quanh bên ngoài của hình trụ. Đây là một công thức tính toán riêng và rất hữu ích trong các bài toán toán học và trong thực tế. Việc biết diện tích xq hình trụ giúp chúng ta hiểu rõ hơn về hình dạng và các đặc tính của hình trụ.
Mục Lục
- Diện tích xq hình trụ được tính như thế nào?
- Diện tích xung quanh hình trụ có công thức tính toán như thế nào?
- Diện tích toàn phần của hình trụ được tính bằng cách nào?
- Có bao nhiêu loại diện tích trong hình trụ và chúng có công thức tính riêng biệt không?
- Nếu biết bán kính đáy và chiều cao của hình trụ, làm thế nào để tính diện tích toàn phần của nó?
- Tính diện tích xung quanh hình trụ nếu đã biết bán kính và chiều cao.
- Tính diện tích xung quanh hình trụ nếu biết diện tích đáy và chiều cao.
- Có những trường hợp nào mà diện tích xung quanh và diện tích toàn phần của hình trụ bằng nhau?
- Diện tích xung quanh hình trụ phụ thuộc vào những yếu tố nào?
- Tại sao diện tích xq hình trụ được tính bằng công thức 2 * π * r * h?
- Công thức tính diện tích xung quanh
- – Khái niệm
- – Công thức
- – Ví dụ
- Công thức tính diện tích toàn phần
- – Giới thiệu
- – Công thức
- – Ví dụ
- Công thức tính thể tích hình trụ tròn
- – Giới thiệu
- – Công thức
- – Ví dụ
- Hình trụ là gì?
- Công thức tính diện tích xung quanh
Diện tích xq hình trụ được tính như thế nào?
Để tính diện tích xung quanh và diện tích toàn phần của một hình trụ, ta sử dụng các công thức sau:1. Diện tích xung quanh (Sxq) của hình trụ:– Công thức: Sxq = 2 * π * r * h– Trong đó: r là bán kính đáy của hình trụ, h là chiều cao của hình trụ2. Diện tích toàn phần (Stp) của hình trụ:– Công thức: Stp = Sxq + 2 * Sđáy– Trong đó: Sđáy là diện tích đáy của hình trụ– Diện tích đáy (Sđáy) có công thức khác nhau tùy thuộc vào hình dạng đáy của hình trụ (ví dụ: hình trụ tròn, hình trụ vuông, hình trụ chữ nhật).Ví dụ: Cho một hình trụ tròn có bán kính đáy r = 4 cm và chiều cao h = 6 cm.– Để tính diện tích xung quanh (Sxq):Sxq = 2 * π * r * h = 2 * 3.14 * 4 * 6 = 150.72 cm2– Để tính diện tích toàn phần (Stp):Trước tiên, ta cần tính diện tích đáy (Sđáy) của hình trụ, với công thức:Sđáy = π * r2 = 3.14 * 4^2 = 50.24 cm2
Sau đó, áp dụng công thức diện tích toàn phần:Stp = Sxq + 2 * Sđáy = 150.72 + 2 * 50.24 = 251.20 cm2Vậy, diện tích xung quanh (Sxq) của hình trụ là 150.72 cm2 và diện tích toàn phần (Stp) là 251.20 cm2.
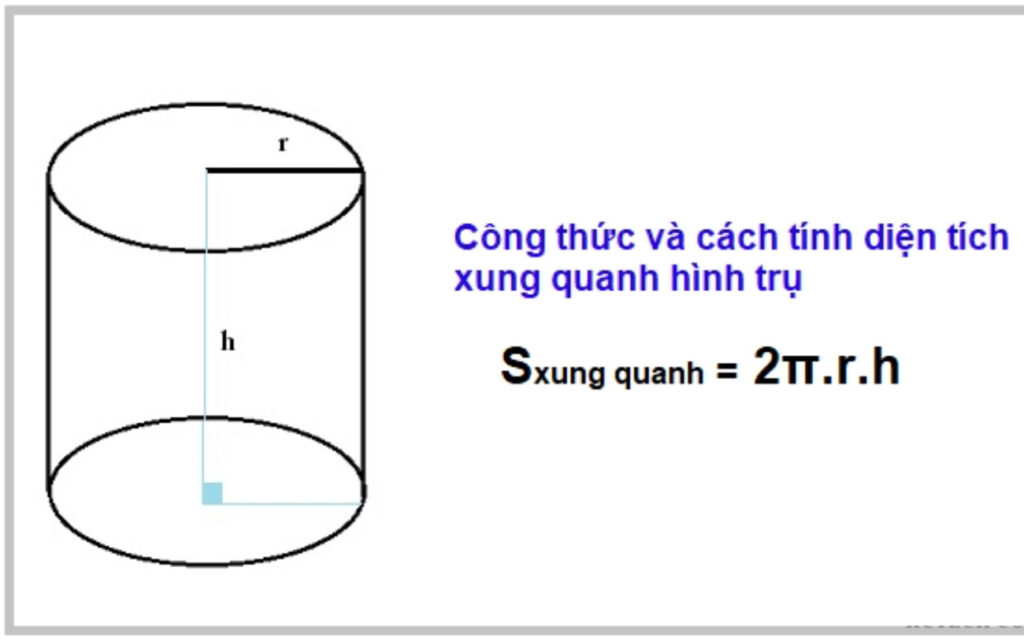
Diện tích xung quanh hình trụ có công thức tính toán như thế nào?
Diện tích xung quanh của một hình trụ có thể được tính bằng công thức sau: Sxq = 2πrh, trong đó π là số pi, r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.Ví dụ, giả sử bán kính đáy của hình trụ là 4 cm và chiều cao của nó là 6 cm. Ta có thể tính diện tích xung quanh bằng công thức trên: Sxq = 2π(4)(6) = 2π(24) = 48π (cm²).Vậy diện tích xung quanh của hình trụ này là 48π cm².Lưu ý rằng đơn vị diện tích (cm²) phụ thuộc vào đơn vị được sử dụng cho bán kính và chiều cao của hình trụ.
Diện tích toàn phần của hình trụ được tính bằng cách nào?
Để tính diện tích toàn phần của một hình trụ, ta sử dụng công thức:S_toan_phan = S_xq + 2 * S_dayTrong đó:– S_xq là diện tích xung quanh hình trụ, được tính bằng công thức: S_xq = 2 * π * r * h, với r là bán kính đáy của hình trụ và h là chiều cao của hình trụ.– S_day là diện tích đáy của hình trụ, được tính bằng công thức: S_day = π * r^2, với r là bán kính đáy của hình trụ.
Ví dụ: Giả sử ta có một hình trụ với bán kính đáy r = 4 cm và chiều cao h = 6 cm. Để tính diện tích toàn phần của hình trụ này, ta thực hiện theo các bước sau:1. Tính diện tích xung quanh hình trụ: S_xq = 2 * π * r * h = 2 * π * 4 * 6 = 48π cm^2 (kết quả xấp xỉ)2. Tính diện tích đáy của hình trụ: S_day = π * r^2 = π * 4^2 = 16π cm^2 (kết quả xấp xỉ)3. Tính diện tích toàn phần của hình trụ: S_toan_phan = S_xq + 2 * S_day = 48π + 2 * 16π = 80π cm^2 (kết quả xấp xỉ)Vậy diện tích toàn phần của hình trụ trong ví dụ này là 80π cm^2 (kết quả xấp xỉ).
Có bao nhiêu loại diện tích trong hình trụ và chúng có công thức tính riêng biệt không?
Trong hình trụ, chúng ta có hai loại diện tích, đó là diện tích xung quanh và diện tích toàn phần. Cả hai loại diện tích này được tính theo công thức riêng biệt.1. Diện tích xung quanh (Sxq) là phần diện tích bao quanh bên ngoài của hình trụ. Để tính diện tích xung quanh, chúng ta sử dụng công thức sau: Sxq = 2 * π * r * h, trong đó r là bán kính của đáy hình trụ và h là chiều cao của hình trụ.2. Diện tích toàn phần (Stp) là tổng thể của diện tích xung quanh và diện tích đáy của hình trụ. Để tính diện tích toàn phần, chúng ta sử dụng công thức sau: Stp = Sxq + 2 * Sđáy. Công thức này có thể tổng quát hơn, tùy thuộc vào hình dạng của đáy hình trụ. Đối với hình trụ tròn, diện tích đáy (Sđáy) được tính bằng π * r^2, trong đó r là bán kính đáy của hình trụ.Vì vậy, có hai loại diện tích trong hình trụ và chúng có công thức tính riêng biệt.
Nếu biết bán kính đáy và chiều cao của hình trụ, làm thế nào để tính diện tích toàn phần của nó?
Để tính diện tích toàn phần của hình trụ, ta có thể làm theo các bước sau:Bước 1: Xác định bán kính đáy (r) và chiều cao (h) của hình trụ.
Bước 2: Tính diện tích xung quanh (Sxq) của hình trụ bằng công thức:Sxq = 2 * π * r * hBước 3: Tính diện tích các đáy (Sđáy) của hình trụ bằng công thức:Sđáy = π * r^2Bước 4: Tính diện tích toàn phần (Stp) của hình trụ bằng công thức:Stp = Sxq + 2 * SđáyVí dụ: Cho một hình trụ có bán kính đáy r = 4 cm và chiều cao h = 6 cm.Tính diện tích toàn phần của hình trụ:Bước 1: r = 4 cm, h = 6 cmBước 2: Tính diện tích xung quanh:Sxq = 2 * π * r * h = 2 * 3.14 * 4 * 6 = 150.72 cm^2Bước 3: Tính diện tích đáy:Sđáy = π * r^2 = 3.14 * 4^2 = 50.24 cm^2Bước 4: Tính diện tích toàn phần:Stp = Sxq + 2 * Sđáy = 150.72 + 2 * 50.24 = 251.20 cm^2Vậy diện tích toàn phần của hình trụ là 251.20 cm^2.

Tính diện tích xung quanh hình trụ nếu đã biết bán kính và chiều cao.
Để tính diện tích xung quanh hình trụ nếu đã biết bán kính và chiều cao, ta có công thức:Diện tích xung quanh hình trụ = 2 * π * r * hTrong đó:– π là giá trị xấp xỉ của số Pi, có giá trị là khoảng 3.14.– r là bán kính đáy của hình trụ.– h là chiều cao của hình trụ.Cách tính diện tích xung quanh hình trụ sẽ được thực hiện như sau:1. Gán giá trị cho bán kính đáy (r) và chiều cao (h) của hình trụ.2. Tính tích của 2, π, r và h.3. Nhân kết quả từ bước 2 với 2.4. Nhân kết quả từ bước 3 với giá trị của Pi (khoảng 3.14).5. Kết quả thu được chính là diện tích xung quanh hình trụ.Ví dụ:Giả sử hình trụ có bán kính đáy r = 4 cm và chiều cao h = 6 cm.– Áp dụng công thức: Diện tích xung quanh hình trụ = 2 * π * r * h.– Gán giá trị vào công thức: Diện tích xung quanh hình trụ = 2 * 3.14 * 4 * 6.– Tính toán: Diện tích xung quanh hình trụ = 150.72 (khoảng).Vậy, diện tích xung quanh hình trụ trong trường hợp này là khoảng 150.72 (khoảng).
Tính diện tích xung quanh hình trụ nếu biết diện tích đáy và chiều cao.
Để tính diện tích xung quanh của một hình trụ, ta cần biết diện tích đáy và chiều cao của hình trụ.Bước 1: Đầu tiên, ta xác định diện tích đáy của hình trụ. Diện tích đáy được tính bằng công thức của diện tích hình dạng đáy tương ứng, ví dụ như hình tròn thì diện tích đáy làSđáy = π * r^2Trong đó, r là bán kính của đáy.Bước 2: Tiếp theo, ta tính diện tích xung quanh. Diện tích xung quanh của hình trụ là phần diện tích bao quanh bên ngoài của hình trụ. Công thức tính diện tích xung quanh của hình trụ làSxq = 2 * π * r * hTrong đó, r là bán kính của đáy và h là chiều cao của hình trụ.Ví dụ: Giả sử diện tích đáy của một hình trụ là 20 cm^2 và chiều cao là 10 cm.Bước 1: Diện tích đáy là Sđáy = 20 cm^2.Bước 2: Diện tích xung quanh là Sxq = 2 * π * r * h = 2 * π * √(20/π) * 10 = 40√(20/π) cm^2 (kết quả có thể được làm tròn).Vậy, diện tích xung quanh của hình trụ nếu biết diện tích đáy là 20 cm^2 và chiều cao là 10 cm là 40√(20/π) cm^2.

Có những trường hợp nào mà diện tích xung quanh và diện tích toàn phần của hình trụ bằng nhau?
Diện tích xung quanh và diện tích toàn phần của một hình trụ bằng nhau trong các trường hợp sau đây:– Khi chiều cao của hình trụ bằng 0: Nếu chiều cao của hình trụ là 0, diện tích xung quanh và diện tích toàn phần của hình trụ sẽ bằng 0 do không có bề mặt nào tồn tại.– Khi chiều cao của hình trụ bằng ấn định số hợp lý: Nếu chiều cao của hình trụ được chọn sao cho tổng của chiều cao và bán kính đáy là một giá trị hợp lý, diện tích xung quanh và diện tích toàn phần có thể bằng nhau.Ví dụ: Xét hình trụ có bán kính đáy r và chiều cao h. Khi r + h = một giá trị cố định như π, diện tích xung quanh và diện tích toàn phần của hình trụ sẽ bằng nhau.Tuy nhiên, trường hợp này không áp dụng cho tất cả các loại hình trụ mà chỉ áp dụng cho một số trường hợp cụ thể. Để tính toán diện tích xung quanh và diện tích toàn phần của hình trụ, ta cần biết công thức tính diện tích của từng loại diện tích.
Diện tích xung quanh hình trụ phụ thuộc vào những yếu tố nào?
Diện tích xung quanh của hình trụ phụ thuộc vào ba yếu tố chính là bán kính đáy (r), chiều cao (h), và hằng số π (pi). Công thức để tính diện tích xung quanh của hình trụ là: Sxq = 2πrh. Trong đó, π là hằng số PI, có giá trị xấp xỉ là 3.14. Bán kính đáy (r) là khoảng cách từ trung tâm đáy của hình trụ đến một điểm trên đường viền đáy. Chiều cao (h) là khoảng cách từ mặt đáy hình trụ đến mặt đỉnh của hình trụ.
Tại sao diện tích xq hình trụ được tính bằng công thức 2 * π * r * h?
Diện tích xung quanh (xq) của một hình trụ được tính bằng công thức 2 * π * r * h vì công thức này tính toán diện tích của hình trụ bao gồm phần diện tích bao quanh bên ngoài hình trụ.Trong công thức này, π biểu thị cho số Pi (khoảng 3.14159) là một hằng số được sử dụng để tính toán diện tích các hình tròn, và r biểu thị bán kính đáy của hình trụ.
Hơn nữa, h biểu thị cho chiều cao của hình trụ. Khi nhân r và h, ta tính được diện tích xq của hình trụ.Công thức này cũng có thể được xem như là sự giao nhau giữa diện tích toàn phần (được tính bằng công thức 2 * π * r * (r + h)) và diện tích đáy (được tính bằng công thức π * r^2).Tuy nhiên, cần lưu ý rằng công thức này chỉ áp dụng cho hình trụ và không áp dụng cho các hình khác như hình cầu hay hình nón.
Công thức tính diện tích xung quanh
– Khái niệm
Diện tích xung quanh hình trụ tròn chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ tròn, không gồm diện tích hai đáy.
Diện tích hình trụ thường được nhắc đến với 2 khái niệm: xung quanh và toàn phần.
- Diện tích xung quanh hình trụ chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ, không gồm diện tích hai đáy.
- Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.
– Công thức
Công thức tính diện tích xung quanh bằng chu vi đường tròn đáy nhân với chiều cao.
Sxq = 2.π.r.h
Trong đó:
– r: Bán kính hình trụ.
– h: Chiều cao nối từ đáy tới đỉnh hình trụ.
– π = 3.14159265359

– Ví dụ
Một hình trụ tròn có bán kính đáy r = 5 cm, chiều cao h = 7cm. Tính diện tích xung quanh hình trụ đứng.
Hướng dẫn giải: Diện tích xung quanh của hình trụ tròn: Sxq = 2.π.r.h = 2π.5.7 = 70π = 219,8 (cm2).
Ví dụ 1: Một bóng đèn huỳnh quang dài 1,2m, đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng hình hộp (h.82). Tính diện tích phần giấy cứng dùng để làm một hộp.
Lời giải:
Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Diện tích xung quanh của hình hộp chính là diện tích bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm::
Sxq= 4.4.120 = 1920 cm2
Ví dụ 2: Mô hình của một cái lọ thí nghiệm dạng hình trụ (không nắp) có bán kính đường tròn đáy 14cm,chiều cao 10cm. Tìm diện tích xung quanh cộng với diện tích một đáy
Lời giải:

Công thức tính diện tích toàn phần
– Giới thiệu
Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.
– Công thức
Công thức tính diện tích 2 đường tròn đáy
S2đ=2πr2(Sđ=πr2)
Công thức tính diện tích toàn phần bằng diện tích xung quanh cộng với diện tích của 2 đáy.
Stp = Sxq + 2.Sđáy = 2.π.r2 + 2.π.r.h
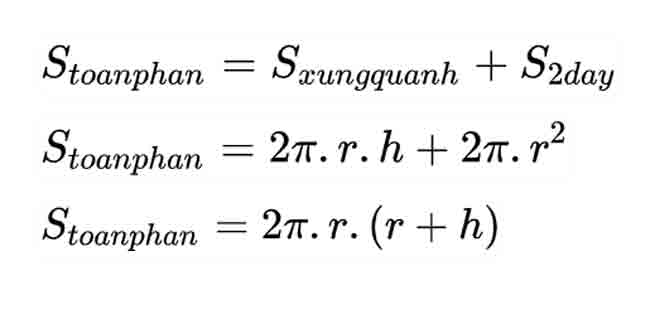
Trong đó:
– r: Bán kính hình trụ.
– h: Chiều cao hình trụ.
– π = 3.14159265359

– Ví dụ
Một hình trụ tròn có bán kính đáy r = 4 cm, chiều cao h = 6 cm. Tính diện tích toàn phần hình trụ đứng.
Hướng dẫn giải: Stp = Sxq + 2.Sđáy= 2.π.r2 + 2.π.r.h = 2.π.42 + 2.π.4.6 = 32π + 48π = 80π (cm2).
Ví Dụ Cách Tính Diện Tích Hình Trụ:
Cho một hình trụ có bán kính đường tròn đáy là 6 cm , trong khi đó chiều cao nối từ đáy tới đỉnh hình trụ dày 8 cm. Hỏi diện tích xung quanh và diện tích toàn phần của hình trụ bằng bao nhiêu?
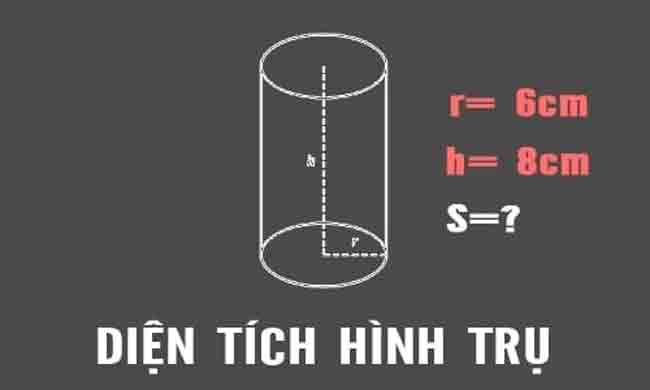
Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm . Suy ra ta có công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ bằng:
– Diện tích xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm2
– Diện tích toàn phần hình trụ = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm2.
Ví dụ
Ví dụ 1: Tính diện tích toàn phần của hình trụ, có độ dài đường tròn đáy là 10cm, khoảng cách giữa 2 đáy là 6cm.

Giải
Theo đề bài ta có: h = 6cm; 2r = 10cm => r = 5cm.
Áp dụng công thức tính diện tích toàn phần hình trụ:
Stp=2πr(r+h)=2π.5(5+6)=110π(cm2)
=> Vậy diện tích toàn phần của hình trụ là 110π(cm2)
Ví dụ 2: Tính diện tích toàn phần của hình trụ có chiều cao là 7cm và diện tích xung quanh bằng 310 (cm2)

Giải
Theo đề bài ta có: h = 7; Sxq=310
Áp dụng công thức tính diện tích xung quanh Sxq=2πrh
=> r=Sxq2πrh=3102π.7≈7cm
Vậy Sđ=πr2=π.72=49π≈154cm2
=> Diện tích toàn phần của hình trụ: Stp=2.Sđ+Sxq=2.154+310=618cm2
Công thức tính thể tích hình trụ tròn
– Giới thiệu
Thể tích hình trụ tròn là lượng không gian mà nó chiếm.
– Công thức
Công thức tính thể tích hình trụ tròn bằng diện tích của mặt đáy nhân với chiều cao.
V = π.r2.h.
Trong đó:
– r: Bán kính hình trụ.
– h: Chiều cao nối từ đáy tới đỉnh hình trụ.
– π = 3.14159265359

– Ví dụ
Một hình trụ tròn có bán kính đáy r = 8 cm, chiều cao h = 6 cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ.
Hướng dẫn giải: Thể tích khối trụ: V = π.r2.h = π.64.6 = 384π (cm3).
– Ví Dụ Cách Tính Diện Tích Hình Trụ:
Cho một lăng trụ bất kỳ có bán kính mặt đáy r = 4 cm , trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 8 cm . Hỏi thể tích của hình trụ này bằng bao nhiêu?

Theo đó, ta áp dụng vào công thức tính thể tích hình trụ và có: bán kính mặt đáy hình trụ r = 4cm và chiều cao hình trụ h = 8cm. Suy ra, ta có công thức tính thể tích hình trụ như sau:
V = π x r2 x h = π x 42 x 8 = ~ 402 cm3
Ví dụ 2: Một hình trụ có chu vi đáy bằng 20 cm, diện tích xung quanh bằng 14 cm2. Tính chiều cao của hình trụ và thể tích của hình trụ.
Lời giải:
Diện tích xung quanh của hình trụ: Sxq = chu vi đáy x chiều cao = 2 x π x r x h = 20 x h = 14
→ h = 0,7 (cm)
Chu vi đáy bằng 20cm → 2 x π x r = 20 → r ~ 3,18 cm
Thể tích của hình trụ: V = π x r2 x h ~ 219,91 cm3
Ví dụ 3: Một hình trụ có diện tích toàn phần gấp 2 lần diện tích xung quanh biết bán kính đáy hình trụ là 6cm. Tính thể tích hình trụ.
Lời giải:
Diện tích toàn phần gấp 2 lần diện tích xung quanh: Stp = 2Sxq
→ 2 x 2 x π x r x h = 2 x π x r x (r + h) → 2h = 6 + h → h = 6 (cm)
Thể tích của hình trụ: V = π x r2 x h ~ 678,58 cm3
Hình trụ là gì?
Hình trụ là hình được giới hạn bởi hai đường tròn có đường kính bằng nhau và mặt trụ.

Hình trụ tròn là hình trụ khi quay hình chữ nhật quanh trục cố định, 2 đáy là hình tròn bằng nhau và song song với nhau.
Hình trụ tròn là hình trụ có 2 đáy là hình tròn bằng nhau và song song với nhau. Hình trụ được sử dụng khá phổ biến trong các bài toán hình học từ căn bản đến phức tạp, trong đó công thức tính diện tích, thể tích hình trụ thường được sử dụng khác phổ biến. Nếu bạn đã biết cách tính diện tích và chu vi hình tròn thì cũng có thể dễ dàng suy luận ra các công thức tính thể tích, diện tích xung quanh cũng như diện tích toàn phần của hình trụ.
Công thức toán
Gia sư môn toán
CÔNG THỨC ĐẠO HÀM
Công thức tính diện tích xung quanh hình trụ
Công thức tính diện tích mặt cầu
Từ khóa » Công Thức Diện Tích Toàn Phần Khối Trụ
-
Diện Tích Toàn Phần Hình Trụ Tròn Xoay Là Gì ? Cách Tính Kèm Ví Dụ ...
-
Công Thức Tính Thể Tích Hình Trụ, Diện Tích Xung Quanh Hình Trụ Và Toà
-
Diện Tích Xung Quanh Hình Trụ, Diện Tích Toàn Phần Hình Trụ
-
Công Thức Tính Diện Tích Xung Quanh Hình Trụ - THPT Sóc Trăng
-
Công Thức Tính Thể Tích Hình Trụ, Diện Tích Xung Quanh Và Toàn Phần ...
-
Cách Tính Diện Tích Toàn Phần Hình Trụ
-
Công Thức Diện Tích Toàn Phần Hình Trụ Chi Tiết Nhất - Top Lời Giải
-
Diện Tích Xung Quanh Hình Trụ, Toàn Phần Hình Trụ Có VD Minh Họa
-
Công Thức Tính Diện Tích Xung Quanh Hình Trụ Và Toàn Phần Hình Trụ Tròn
-
Công Thức Tính Diện Tích Toàn Phần Hình Trụ Có Bán Kính (r ) Và
-
Diện Tích Xung Quanh Hình Trụ Tính Như Thế Nào? - Toán Thầy Định
-
Công Thức Tính Diện Tích, Thể Tích Hình Trụ Như Thế Nào?
-
Diện Tích Xung Quanh Hình Trụ, Thể Tích Hình Trụ