Công Thức Tính độ Dài đường Trung Tuyến
Có thể bạn quan tâm
GiaiToan.com biên soạn và đăng tải tài liệu Công thức độ dài đường trung tuyến bao gồm các kiến thức: định nghĩa, tính chất đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều và công thức tính đường trung tuyến, giúp các em học sinh củng cố, nắm chắc kiến thức cơ bản Toán 10. Chúc các bạn học tập tốt!
Công thức tính độ dài đường trung tuyến
- A. Đường trung tuyến
- B. Tính chất đường trung tuyến
- a. Tính chất đường trung tuyến của tam giác
- b. Tính chất đường trung tuyến trong tam giác vuông
- c. Đường trung tuyến trong tam giác cân
- C. Công thức tính đường trung tuyến
- D. Bài tập tính độ dài đường trung tuyến trong tam giác
A. Đường trung tuyến
- Đường trung tuyến của 1 đoạn thẳng là 1 đường thẳng đi qua trung điểm của đường thẳng đó.
- Đường trung tuyến trong tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của các cạnh đối diện nó. Mỗi tam giác có 3 đường trung tuyến.
B. Tính chất đường trung tuyến
a. Tính chất đường trung tuyến của tam giác
- Ba đường trung tuyến của tam giác đồng quy tại một điểm được gọi là trọng tâm.
- Khoảng cách từ trong tâm đến mỗi đỉnh của tam giác bằng ![]() đường trung tuyến tương ứng với đỉnh đó.
đường trung tuyến tương ứng với đỉnh đó.
- Khoảng cách từ trong tâm đến trung điểm mỗi cạnh bằng ![]() đường trung tuyến tương ứng với điểm đó.
đường trung tuyến tương ứng với điểm đó.
Ví dụ: Cho tam giác ABC, có D, E, F lần lượt là trung điểm của các cạnh AC, AB, BC.
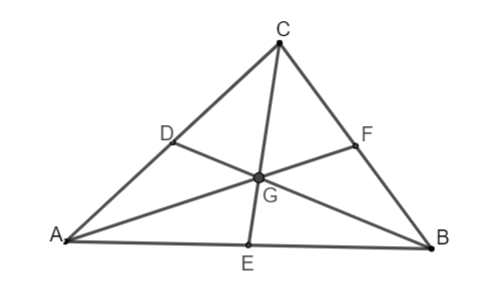 | - Gọi G là giao điểm của các đường thẳng BD, AF, CE suy ra G là trọng tâm tam giác ABC. Ta có các tính chất sau:
|
b. Tính chất đường trung tuyến trong tam giác vuông
- Đường trung tuyến của tam giác vuông có các tính chất chung của đường trung tuyến trong tam giác thường. Ngoài ra ta có các tính chất đặc trưng sau:
+ Đường trung tuyến trong tam giác vuông ứng với cạnh huyền bằng một nửa cạnh huyền.
Ví dụ: Cho tam giác ABC vuông tại C, đường trung tuyến CD
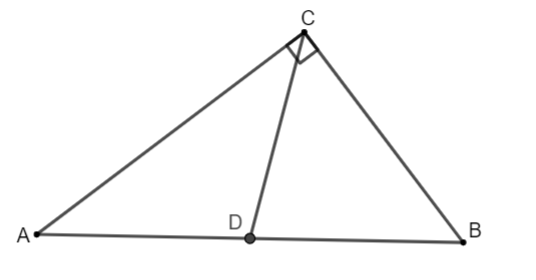 |  |
+ Trong một tam giác có đường trung tuyến ứng với một cạnh mà bằng một nửa cạnh đó thì tam giác đó là tam giác vuông.
c. Đường trung tuyến trong tam giác cân
- Trong tam giác cân, tam giác đều, đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đó và chia tam giác thành hai tam giác bằng nhau.
C. Công thức tính đường trung tuyến
- Cho tam giác ABC có độ dài các cạnh AB = c; AC = b; BC = a, các đường trung tuyến ![]()
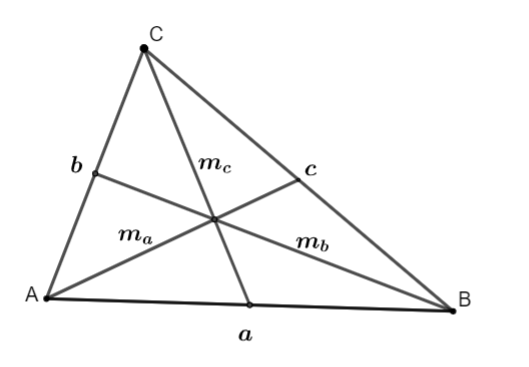 |  |
Ví dụ 1: Tam giác ABC có AB = AC = 10cm, BC = 12cm. Tính độ dài đường trung tuyến AM.
Hướng dẫn giải
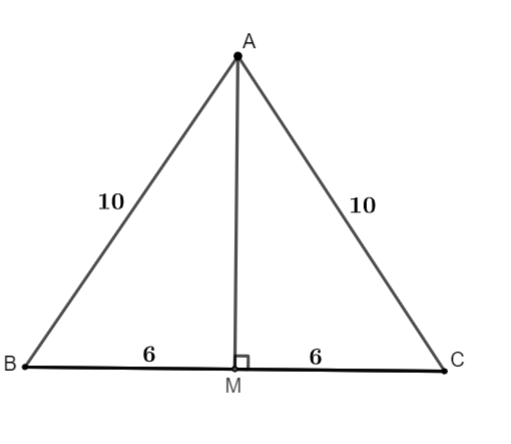 | Ta có tam giác ABC cân tại A, AM là trung tuyến suy ra AM là đường cao, đường phân giác của tam giác ABC
Áp dụng định lý Pi – ta – go cho tam giác vuông AMC có:
|
Ví dụ 2: Tính độ dài đường trung tuyến AM của tam giác ABC có góc , AB = 4cm, AC = 6cm.
Hướng dẫn giải
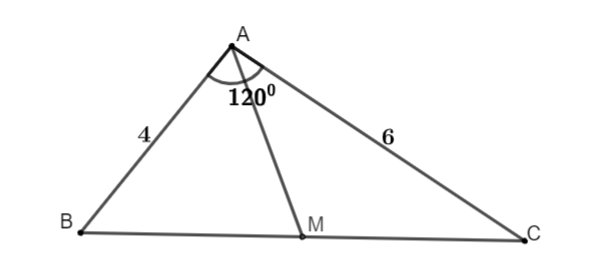 | Ta có:
|
Ví dụ 3: Cho tam giác ABC vuông tại A có độ dài hai đường trung tuyến AM và BN lần lượt bằng 6cm và 9cm. Tính độ dài cạnh AB.
Hướng dẫn giải
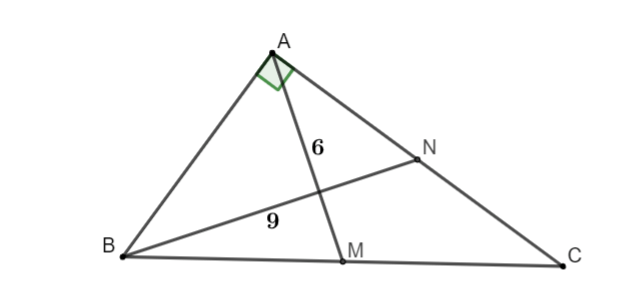
Tam giác ABC vuông tại A, AM là trung tuyến nên AM = BM = MC = 6
Suy ra BC = 12
Mặt khác

D. Bài tập tính độ dài đường trung tuyến trong tam giác
Bài 1:Tính độ dài đường trung tuyến AM của tam giác ABC có góc A = 120 độ, AB = 4cm, AC = 6cm
Bài 2: Cho tam giác ABC có góc BAC bằng 1200, AB = 2a, AC = 3a
a. Tính độ dài cạnh BC, đường trung tuyến AM
b. Tính bán kính đường tròn ngoại tiếp tam giác ABC
c. Gọi D là chân đường phân giác trong góc ABC. Tính diện tích tam giác BDA.
Bài 3: Cho tam giác MNP cân tại M với đường trung tuyến MK (M ∈ NP)
a. Chứng minh tam giác MKN bằng tam giác MKP
b. Biết MN = MP = 13cm, NK = 5cm. Hãy tính độ dài đường trung tuyến MK
Bài 4: Cho tam giác ABC có AB = 6cm, AC = 8cm, góc A = 60°
a. Tính độ dài cạnh BC, diện tích và đường cao AH của tam giác
b. Tính bán kính đường tròn nội tiếp, ngoại tiếp tam giác ABC, độ dài trung tuyến BM của tam giác.
Từ khóa » Công Thức đường Trung Tuyến Trong Tam Giác
-
Đường Trung Tuyến Là Gì? Tính Chất, Công Thức Tính đường Trung Tuyến
-
Công Thức Tính độ Dài Trung Tuyến Trong Tam Giác & Các Dạng Bài Tập
-
Công Thức Tính độ Dài đường Trung Tuyến Và Bài Tập Có Lời Giải
-
Công Thức, Cách Tính độ Dài đường Trung Tuyến Cực Hay, Chi Tiết
-
Công Thức Tính độ Dài đường Trung Tuyến
-
Công Thức Tính đường Trung Tuyến Trong Tam Giác
-
Công Thức Tính độ Dài đường Trung Tuyến Ôn Tập Toán 10
-
Công Thức Tính đường Trung Tuyến Trong Tam Giác Và Bài Tập Có Lời Giải
-
Công Thức Tính độ Dài đường Trung Tuyến Và Bài Tập Minh Họa
-
[CHUẨN NHẤT] Công Thức Tính độ Dài đường Trung Tuyến - TopLoigiai
-
Công Thức độ Dài đường Trung Tuyến - Thayphu
-
Công Thức Đường Trung Tuyến Trong Tam Giác & Các Dạng Bài Tập
-
Đường Trung Tuyến: Lý Thuyết, Tính Chất, Công Thức Tính Trong Tam Giác