Công Thức Tính đường Chéo Hình Chữ Nhật
Có thể bạn quan tâm
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ ZaloTính độ dài đường chéo hình chữ nhật
- A. Định nghĩa hình chữ nhật
- B. Tính chất hình chữ nhật
- C. Dấu hiệu nhận biết hình chữ nhật
- D. Cách tính đường chéo hình chữ nhật
- E. Bài tập tính độ dài đường chéo hình chữ nhật
- Lời giải bài tập tính đường chéo hình chữ nhật
Đường chéo hình chữ nhật là đường thẳng nối hai góc đối diện của hình chữ nhật. Mỗi hình chữ nhật có hai đường chéo với độ dài bằng nhau. Trong bài viết này VnDoc xin mời các em học sinh cùng tham khảo cách tính độ dài đường chéo của hình chữ nhật cũng như các tính chất và dấu hiệu nhận biết hình chữ nhật nhé.
Công thức tính đường chéo hình bình hành
Công thức tính nhanh Hình học
A. Định nghĩa hình chữ nhật
+ Hình chữ nhật là tứ giác có 4 góc vuông.
B. Tính chất hình chữ nhật
+ Hình chữ nhật cũng là hình bình hành, cũng là hình thang cân nên hình chữ nhật có đầy đủ tính chất của hình bình hành và hình thang cân.
+ Bởi vậy, từ tính chất hai đường chéo bằng nhau của hình thang cân và hai đường chéo cắt nhau tại trung điểm mỗi đường của hình bình hành, ta có:
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
C. Dấu hiệu nhận biết hình chữ nhật
+ Mỗi dạng hình học có các dấu hiệu nhận biết riêng. Với hình chữ nhật, ta sẽ dựa vào 4 dấu hiệu sau:
1. Tứ giác có ba góc vuông là hình chữ nhật
2. Hình thang cân có một góc vuông là hình chữ nhật.
3. Hình bình hành có một góc vuông là hình chữ nhật.
4. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
D. Cách tính đường chéo hình chữ nhật
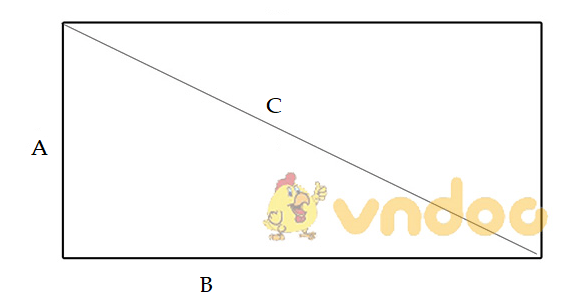
Vì đường chéo hình chữ nhật chia hình chữ nhật thành hai tam giác vuông có cùng kích thước nên ta sẽ sử dụng Định lý Pytago trong tam giác vuông để tính độ dài của đường chéo hình chữ nhật.
+ Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là A và B. Độ dài đường chéo hình chữ nhật là C. Khi đó ta có:
![]() \({A^2} + {B^2} = {C^2}\)
\({A^2} + {B^2} = {C^2}\)
Ví dụ minh họa:
Điền vào chỗ trống, biết rằng a, b là chiều dài và chiều rộng của hình chữ nhật và d là độ dài đường chéo của một hình chữ nhật.
| a | 5 | ||
| b | 12 | ||
| d | 7 |
Lời giải:
Đường chéo chia hình chữ nhật thành hai tam giác vuông với hai cạnh góc vuông có độ dài là a và b; độ dài cạnh huyền là d.
Áp dụng định lí Pi-ta-go vào các tam giác vuông tương ứng để tính các cạnh còn lại bằng công thức ![]() \({d^2} = {a^2} + {b^2}\)
\({d^2} = {a^2} + {b^2}\)
- Với a = 5 và b = 12 thì ![]() \({d^2} = {5^2} + {12^2} = 169 \Rightarrow d = 13\) (đơn vị độ dài).
\({d^2} = {5^2} + {12^2} = 169 \Rightarrow d = 13\) (đơn vị độ dài).
- Với ![]() \(b = \sqrt 6\) và
\(b = \sqrt 6\) và ![]() \(d = \sqrt {10}\) thì
\(d = \sqrt {10}\) thì ![]() \({d^2} = {a^2} + {b^2} \Rightarrow {a^2} = {d^2} - {b^2} = 10 - 6 = 4 \Rightarrow a = 2\) (đơn vị độ dài)
\({d^2} = {a^2} + {b^2} \Rightarrow {a^2} = {d^2} - {b^2} = 10 - 6 = 4 \Rightarrow a = 2\) (đơn vị độ dài)
- Với ![]() \(a = \sqrt {13}\) và thì
\(a = \sqrt {13}\) và thì ![]() \({d^2} = {a^2} + {b^2} \Rightarrow {b^2} = {d^2} - {a^2} = 49 - 13 = 36 \Rightarrow b = 6\) (đơn vị đồ dài)
\({d^2} = {a^2} + {b^2} \Rightarrow {b^2} = {d^2} - {a^2} = 49 - 13 = 36 \Rightarrow b = 6\) (đơn vị đồ dài)
Cuối cùng, ta có kết quả như sau:
| a | 5 | 2 | |
| b | 12 | 6 | |
| d | 13 | 7 |
E. Bài tập tính độ dài đường chéo hình chữ nhật
Bài 1: Tính độ dài đường chéo hình chữ nhật biết chiều dài bằng 10dm và chiều rộng bằng 5dm.
Bài 2: Đường chéo của hình chữ nhật dài bằng 13m, chiều dài hơn chiều rộng 7m. Tính chu vi và diện tích của hình chữ nhật đó.
Bài 3: Cho hình chữ nhật có chu vi bằng 28cm, hai cạnh của nó hơn kém nhau 2cm. Tính độ dài đường chéo của hình chữ nhật đó
Bài 4: Một hình chữ nhật có chu vi bằng 32m và diện tích bằng 60m2. Tính độ dài đường chéo của hình chữ nhật đó.
Lời giải bài tập tính đường chéo hình chữ nhật
Bài 1:
Gọi độ dài đường chéo hình chữ nhật là a (a > 0, dm)
Áp dụng định lý Pitago, độ dài đường chéo của hình chữ nhật là:
![]() \({a^2} = {10^2} + {5^2} = 125 \Rightarrow a = 5\sqrt 5\)(dm)
\({a^2} = {10^2} + {5^2} = 125 \Rightarrow a = 5\sqrt 5\)(dm)
Bài 2:
Gọi chiều rộng của hình chữ nhật là a (a > 0, m)
Chiều dài của hình chữ nhật là a + 7 (m)
Vì đường chéo hình chữ nhật bằng 13m nên theo áp dụng định lý Pitago có:
 \(\begin{array}{l} {a^2} + {\left( {a + 7} \right)^2} = {13^2}\\ \Leftrightarrow 2{a^2} + 14a - 120 = 0\\ \Leftrightarrow \left[ \begin{array}{l} a = 5\left( {tm} \right)\\ a = - 12\left( L \right) \end{array} \right. \end{array}\)
\(\begin{array}{l} {a^2} + {\left( {a + 7} \right)^2} = {13^2}\\ \Leftrightarrow 2{a^2} + 14a - 120 = 0\\ \Leftrightarrow \left[ \begin{array}{l} a = 5\left( {tm} \right)\\ a = - 12\left( L \right) \end{array} \right. \end{array}\)
Vậy chiều rộng của hình chữ nhật là 5m và chiều dài của hình chữ nhật là 12m.
Chu vi của hình chữ nhật đó là: (5 + 12).2 = 34m
Diện tích của hình chữ nhật đó là: 12.5 = 60m2
Bài 3:
Gọi chiều rộng của hình chữ nhật là a (a > 0, m)
Chiều dài của hình chữ nhật là a + 2 (m)
Chu vi hình chữ nhật bằng 28cm nên ta có (a + a + 2).2 = 28 => a = 6 (thỏa mãn)
Vậy chiều rộng của hình chữ nhật là 6m và chiều dài của hình chữ nhật là 8m.
Gọi độ dài đường chéo của hình chữ nhật là d. Khi đó áp dụng định lý Pitago ta có:
![]() \({d^2} = {6^2} + {8^2} = 100 \Rightarrow d = 10\)m
\({d^2} = {6^2} + {8^2} = 100 \Rightarrow d = 10\)m
Bài 4:
Nửa chu vi của hình chữ nhật bằng 32 : 2 = 16 (m)
Gọi chiều rộng của hình chữ nhật là a (0 < a < 16, m)
Chiều dài của hình chữ nhật là 16 – a (m)
Diện tích của hình chữ nhật bằng 60m2 nên ta có: ![]() \(a\left( {16 - a} \right) = 60 \Leftrightarrow \left[ \begin{array}{l} a = 6\\ a = 10 \end{array} \right.\left( {tm} \right)\)
\(a\left( {16 - a} \right) = 60 \Leftrightarrow \left[ \begin{array}{l} a = 6\\ a = 10 \end{array} \right.\left( {tm} \right)\)
Gọi độ dài đường chéo hình chữ nhật là d
Với a = 6 thì chiều rộng của hình chữ nhật là 6m và chiều dài của hình chữ nhật là 10m. Áp dụng định lý Pitago có: ![]() \({d^2} = {6^2} + {10^2} = 136 \Rightarrow d = 2\sqrt {34}\)(m)
\({d^2} = {6^2} + {10^2} = 136 \Rightarrow d = 2\sqrt {34}\)(m)
Với a = 10 thì chiều rộng của hình chữ nhật là 10m và chiều dài của hình chữ nhật là 6m. Áp dụng định lý Pitago có: ![]() \({d^2} = {6^2} + {10^2} = 136 \Rightarrow d = 2\sqrt {34}\) (m)
\({d^2} = {6^2} + {10^2} = 136 \Rightarrow d = 2\sqrt {34}\) (m)
------------
Trên đây, VnDoc đã giới thiệu tới thầy cô và các em học sinh tài liệu Công thức tính độ dài đường chéo hình chữ nhật. Ngoài ra, mời các bạn tham khảo thêm các tài liệu học tập các lớp như: Tài liệu học tập lớp 8, Tài liệu học tập lớp 9, ....
Tham khảo thêm
-
Công thức tính trọng lượng riêng
-
Công thức tính lực ma sát
-
Công thức tính cường độ dòng điện
-
Công thức tính tiết diện dây dẫn điện 3 pha
-
Công thức tính lãi kép
-
Công thức tính NPV
-
Công thức tính độ dài đường trung tuyến
-
Công thức tính thể tích hình chóp cụt, hình nón cụt
-
Công thức tính hiệu suất phản ứng hóa học
-
Công thức giải nhanh cấp số cộng và cấp số nhân
-
Công thức tính điện trở
-
Công thức tính điện năng tiêu thụ
Từ khóa » Công Thức đường Chéo Hình Chữ Nhật
-
Công Thức Tính đường Chéo Hình Chữ Nhật Chuẩn 100% [Bài Tập ...
-
Cách Tính đường Chéo Hình Chữ Nhật Khi Biết độ Dài 2 Cạnh Hoặc ...
-
Công Thức Tính đường Chéo Hình Chữ Nhật Nhanh, Chinh Xác Nhất
-
Công Thức Tính đường Chéo Hình Vuông, đường Chéo Hình Chữ Nhật
-
Cách để Tìm độ Dài đường Chéo Hình Chữ Nhật - WikiHow
-
Công Thức Cách Tính đường Chéo Trong Hình Chữ Nhật - Kèm Lời Giải
-
Công Thức Tính đường Chéo Hình Chữ Nhật Và Bài Tập Có Lời Giải Từ A Z
-
Công Thức Tính: [Đường Chéo Hình Chữ Nhật] & Bài Tập Tham Khảo
-
Công Thức Tính đường Chéo Hình Chữ Nhật đầy đủ, Chi Tiết, Dễ Hiểu
-
Công Thức Tính độ Dài đường Chéo Hình Chữ Nhật Và Bài Tập Có Lời Giải
-
Tính độ Dài đường Chéo Hình Chữ Nhật
-
Công Thức Tính đường Chéo Hình Chữ Nhật Chuẩn 100 ... - Top1chiase
-
Công Thức Tính đường Chéo Hình Chữ Nhật, Cách Tính, Cho Ví Dụ
-
Công Thức Tính đường Chéo Hình Chữ Nhật