Công Thức Tính GTNN - GTLN Của Hàm Số Lượng Giác Chi Tiết

Công thức tính GTNN - GTLN của hàm số lượng giác chi tiết - Toán lớp 11

1. Lí thuyết

a) Sử dụng tính bị chặn của hàm số lượng giác

−1≤sinu(x)≤1; 0≤sin2u(x)≤1; 0≤sinu(x)≤1

−1≤cosu(x)≤1; 0≤cos2u(x)≤1; 0≤cosu(x)≤1

b) Dạng y = asinx + bcosx + c

Bước 1: Đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]:

y = asinx + bcosx + c=a2+b2aa2+b2sinx+ba2+b2cosx+c

⇔y=a2+b2.sinx+α+c với α thỏa mãn

cosα=aa2+b2;sinα=ba2+b2

Bước 2: Đánh giá −1≤sinx+α≤1∀x∈ℝ

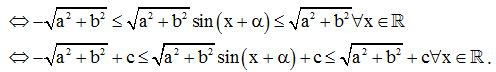
2. Công thức

a) Dạng y = asin[u(x)] + b hoặc y = acos[u(x)] + b

Ta có: −a+b≤y≤a+b

Hàm số có giá trị nhỏ nhất là –|a| + b và giá trị lớn nhất là |a| + b.

b) Dạng y = asin2[u(x)] + b ; y = a|sin[u(x)]| + b;

Dạng y = acos2[u(x)] + b; y = a|cos[u(x)]| + b (với a khác 0)

+ Trường hợp 1: a > 0. Ta có: b≤y≤a+b.

Hàm số có giá trị nhỏ nhất là b và giá trị lớn nhất là a + b.

+ Trường hợp 2: a < 0. Ta có: a+b≤y≤b.

Hàm số có giá trị nhỏ nhất là a + b và giá trị lớn nhất là b.

c) Dạng y = asinx + bcosx + c

Ta có: −a2+b2+c≤y≤a2+b2+c

Hàm số có giá trị nhỏ nhất là −a2+b2+c và giá trị lớn nhất là a2+b2+c.

3. Ví dụ minh họa

Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số sau:

a) y = 3sin(2x+1) – 7

b) y=−2cos2x+π3+1

Lời giải

a) y = 3sin(2x+1) – 7

Cách 1: Áp dụng công thức ta có: −3−7≤y≤3−7⇔−10≤y≤−4

Cách 2: Giải chi tiết

Ta có −1≤sin2x+1≤1∀x∈ℝ

⇔−3≤3sin2x+1≤3∀x∈ℝ⇔−10≤sin2x+1−7≤−4∀x∈ℝ⇔−10≤y≤−4

Vậy giá trị lớn nhất của hàm số là -4 và giá trị nhỏ nhất của hàm số là -10.

b) y=−2cos2x+π3+1

Cách 1: Áp dụng công thức ta có: −2+1≤y≤1⇔−1≤y≤1.

Cách 2: Giải chi tiết

Ta có 0≤cos2x+π3≤1∀x∈ℝ

⇔0≤2cos2x+π3≤2∀x∈ℝ⇔−2≤−2cos2x+π3≤0∀x∈ℝ⇔−1≤−2cos2x+π3+1≤1∀x∈ℝ⇔−1≤y≤1

Vậy giá trị lớn nhất của hàm số là 1 và giá trị nhỏ nhất của hàm số là -1.

Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 5sin2x – 12cosx + 2

Lời giải

Cách 1: Áp dụng công thức ta có:

−52+122+2≤y≤52+122+2⇔−11≤y≤15

Cách 2: Giải chi tiết

Ta có: y = 5sin2x – 12cosx + 2

⇔y=13513sin2x−1213cos2x+2⇔y=13sin2xcosα−cos2xsinα+2

⇔y=13sin2x−α+2 với 513=cosα; 1213=sinα.

Ta có −1≤sin2x−α≤1∀x∈ℝ

⇔−13≤13sin2x−α≤13∀x∈ℝ⇔−11≤13sin2x−α+2≤15∀x∈ℝ⇔−11≤y ≤15

Vậy giá trị lớn nhất của hàm số là 15 và giá trị nhỏ nhất của hàm số là -11.

4. Bài tập tự luyện

Câu 1. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y=7−2cosx+π4lần lượt là:

A. 4 và 7

B. -2 và 7

C. 5 và 9

D. -2 và 2

Câu 2. Giá trị nhỏ nhất và lớn nhất của hàm số y = 4cos2x – 3sin2x + 6 là:

A. 3 và 10

B. 1 và 11

C. 6 và 10

D. -1 và 13

Câu 3. Giá trị lớn nhất và nhỏ nhất của hàm số y = 3 – 2|sinx| lần lượt là

A. 1 và 0

B. 3 và 2

C. 3 và -2

D. 3 và 1

Đáp án:

1 – C, 2 – B, 3 – D

Xem thêm tổng hợp công thức môn Toán lớp 9 đầy đủ và chi tiết khác:

Công thức giải phương trình lượng giác cơ bản

Công thức, cách biến đổi biểu thức a sinx + b cosx

Công thức, cách gộp nghiệm phương trình lượng giác

Công thức hoán vị

Công thức chỉnh hợp