Công Thức Tính Nhanh Khoảng Cách (Tập 2)

Trang chủ » Ct Tính Nhanh Khoảng Cách » Công Thức Tính Nhanh Khoảng Cách (Tập 2)

Có thể bạn quan tâm

      • Mầm non

      • Lớp 1

      • Lớp 2

      • Lớp 3

      • Lớp 4

      • Lớp 5

      • Lớp 6

      • Lớp 7

      • Lớp 8

      • Lớp 9

      • Lớp 10

      • Lớp 11

      • Lớp 12

      • Thi vào lớp 6

      • Thi vào lớp 10

      • Thi Tốt Nghiệp THPT

      • Đánh Giá Năng Lực

      • Khóa Học Trực Tuyến

      • Hỏi bài

      • Trắc nghiệm Online

      • Tiếng Anh

      • Thư viện Học liệu

      • Bài tập Cuối tuần

      • Bài tập Hàng ngày

      • Thư viện Đề thi

      • Giáo án - Bài giảng

      • Tất cả danh mục

    • Mầm non
    • Lớp 1
    • Lớp 2
    • Lớp 3
    • Lớp 4
    • Lớp 5
    • Lớp 6
    • Lớp 7
    • Lớp 8
    • Lớp 9
    • Lớp 10
    • Lớp 11
    • Lớp 12
    • Thi Chuyển Cấp
Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Chọn lớp Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Lưu và trải nghiệm Đóng Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169 VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12 Công thức tính nhanh khoảng cách (Tập 2) Tài liệu luyện thi THPT Quốc gia môn Toán Bài trước Tải về Bài sau Lớp: Lớp 12 Môn: Toán Loại File: PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Công thức tính nhanh khoảng cách (Tập 2)

  • A.Tổng quan bài toán tính khoảng cách từ điểm đến mặt phẳng 
  • B. Bài tập tự luận áp dụng tính khoảng cách từ điểm đến mặt phẳng 
  • C. Bài tập trắc nghiệm áp dụng tính khoảng cách từ điểm đến mặt phẳng 
  • D. Bài tập tính khoảng cách giữa hai đường thẳng chéo nhau 

Công thức tính nhanh khoảng cách (Tập 2) đưa ra công thức và hướng dẫn cách giải các dạng bài tập mở rộng về tìm khoảng cách trong hình học không gian. Hi vọng tài liệu này sẽ giúp các bạn ôn thi đại học môn Toán, luyện thi THPT Quốc gia môn Toán hiệu quả. Mời các bạn cùng tham khảo.

  • Công thức tính nhanh khoảng cách (Tập 1)
  • Bài tập trắc nghiệm thể tích khối đa diện (Có đáp án)
  • Các phương pháp giải Toán hình học không gian

A.Tổng quan bài toán tính khoảng cách từ điểm đến mặt phẳng 

Bài toán tổng quan. Cho hình chóp S.ABC\(S.ABC\) có SA\(SA\) vuông góc mặt phẳng (ABC)\((ABC)\), cho SA = a,S_{\bigtriangleup ABC} = S\(SA = a,S_{\bigtriangleup ABC} = S\) và đường cao của tam giác ABC từ A là h = \frac{2S}{AB}\(h = \frac{2S}{AB}\). Tính khoảng cách từ A đến mặt phẳng (SBC).

Hình vẽ minh họa

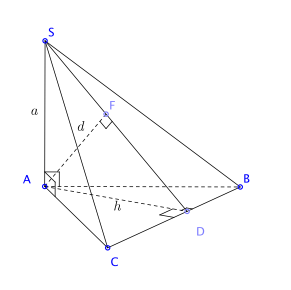
Gọi d\lbrack A,(SBC)\rbrack = d\(d\lbrack A,(SBC)\rbrack = d\). Khi đó: \frac{1}{d^{2}} = \frac{1}{a^{2}} + \frac{1}{h^{2}}\(\frac{1}{d^{2}} = \frac{1}{a^{2}} + \frac{1}{h^{2}}\)

Như vậy, việc tính khoảng cách đưa về tính đường cao của tam giác ABC và diện tích tam giác ABC được tính bằng công thức Herong. Chú ý là trong trường hợp này, tam giác ABC chi là tam giác thường.

B. Bài tập tự luận áp dụng tính khoảng cách từ điểm đến mặt phẳng 

Bài toán 1.  Cho hình chóp S.ABCD\(S.ABCD\) có đáy là hình chữ nhật, SM\bot(ABCD)\(SM\bot(ABCD)\) với M là trung điểm AB. Cho SA = a\sqrt{2},AB = 2a,BC = a\(SA = a\sqrt{2},AB = 2a,BC = a\). Tính khoảng cách từ A đến (SBD)\((SBD)\).

Hướng dẫn giải 

Hình vẽ minh họa:

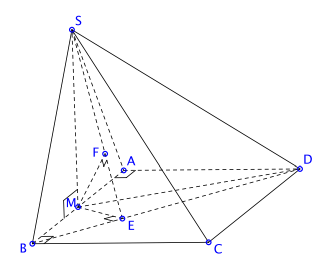
Ta tính d = d\lbrack M,(SBD)\rbrack\(d = d\lbrack M,(SBD)\rbrack\).

Xét khối S.MBD. Đường cao

SM = \sqrt{SA^{2} - AM^{2}} = \sqrt{2a^{2} - a^{2}} = a\(SM = \sqrt{SA^{2} - AM^{2}} = \sqrt{2a^{2} - a^{2}} = a\)

Tính diện tích \bigtriangleup MBD\(\bigtriangleup MBD\) bằng công thức Herong.

Ta có: BM = a,BD = a\sqrt{5},MD = a\sqrt{2}\(BM = a,BD = a\sqrt{5},MD = a\sqrt{2}\).

Suy ra S_{MBD} = \frac{1}{2}a^{2}\(S_{MBD} = \frac{1}{2}a^{2}\).

Khi đó: ME = \frac{2S_{MBD}}{BD} = \frac{a^{2}}{a\sqrt{5}} = \frac{a}{\sqrt{5}}\(ME = \frac{2S_{MBD}}{BD} = \frac{a^{2}}{a\sqrt{5}} = \frac{a}{\sqrt{5}}\).

Sau cùng, \frac{1}{d^{2}} = \frac{1}{ME^{2}} + \frac{1}{SM^{2}} = \frac{5}{a^{2}} + \frac{1}{a^{2}} = \frac{6}{a^{2}} \Rightarrow d = \frac{a}{\sqrt{6}}\(\frac{1}{d^{2}} = \frac{1}{ME^{2}} + \frac{1}{SM^{2}} = \frac{5}{a^{2}} + \frac{1}{a^{2}} = \frac{6}{a^{2}} \Rightarrow d = \frac{a}{\sqrt{6}}\).

Từ đó, d\lbrack A,(SBD)\rbrack = 2d = \frac{2a}{\sqrt{6}}\(d\lbrack A,(SBD)\rbrack = 2d = \frac{2a}{\sqrt{6}}\).

Vậy khoảng cách từ A đến mặt phẳng SBD bằng \frac{2a}{\sqrt{6}}\(\frac{2a}{\sqrt{6}}\).

Nhận xét. Qua ví dụ trên có thể thấy, việc tính khoảng cách từ một điểm bất kỳ sẽ được đưa về khoảng cách từ chân đường cao của hình chóp cần xét. Mặt khác, bước dụng hình chiếu sẽ được bó qua trong thực hành tính toán trắc nghiệm về sau. Ở ví dụ trên, việc tính ME sẽ đơn giản hơn với nhận xét ME bằng một nưa đường cao hạ từ A của tam giác vuông ABD. Tuy nhiên, để bạn đọc làm quen phương pháp cũng như có thuật toán giải quyết bài toán tông quát, chúng tôi vẫn làm theo cách lấy hai lần diện tích chia cạnh đáy.

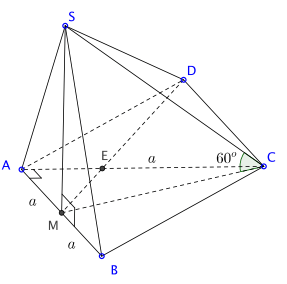
Bài toán 2. Cho hình chóp S.ABCD\(S.ABCD\) có đáy ABCD là hình thoi tâm O canh a góc ABC = 60^{\circ}\(ABC = 60^{\circ}\), hình chiếu của S lên mặt phẳng (ABCD)\((ABCD)\) là điểm M nằm trên AC sao cho AC = 4AM\(AC = 4AM\), góc tạo bời SC vói mặt đáy bằng 60^{\circ}\(60^{\circ}\). Tính khoảng cách từ A đến mặt (SBC).

Hướng dẫn giải 

Hình vẽ minh họa: 

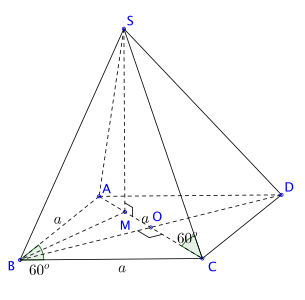
Ta tính d là khoảng cách từ M đến (SBC).

Xét khối chóp S.MBC.

Tam giác ABC đều nên dễ tính được MC = \frac{3a}{4},BM = \frac{a\sqrt{13}}{4},SM = \frac{3\sqrt{3}a}{4}\(MC = \frac{3a}{4},BM = \frac{a\sqrt{13}}{4},SM = \frac{3\sqrt{3}a}{4}\).

Gọi h là đường cao từ M cúa \bigtriangleup MBC\(\bigtriangleup MBC\), khi đó, h \cdot BC = BO \cdot MC\(h \cdot BC = BO \cdot MC\)

Suy ra h = \frac{BO \cdot MC}{BC} =\dfrac{\dfrac{a\sqrt{3}}{2} \cdot \dfrac{3a}{4}}{a} =\dfrac{3a\sqrt{3}}{8}\(h = \frac{BO \cdot MC}{BC} =\dfrac{\dfrac{a\sqrt{3}}{2} \cdot \dfrac{3a}{4}}{a} =\dfrac{3a\sqrt{3}}{8}\).

Từ đó, \frac{1}{d^{2}} = \frac{1}{SM^{2}} + \frac{1}{h^{2}} = \frac{16}{27a^{2}} + \frac{64}{27a^{2}}\(\frac{1}{d^{2}} = \frac{1}{SM^{2}} + \frac{1}{h^{2}} = \frac{16}{27a^{2}} + \frac{64}{27a^{2}}\).

Suy ra: d = \frac{3\sqrt{15}a}{20}\(d = \frac{3\sqrt{15}a}{20}\).

Và có được: d\lbrack A,(SBD)\rbrack = \frac{4}{3}d = \frac{\sqrt{15}a}{5}\(d\lbrack A,(SBD)\rbrack = \frac{4}{3}d = \frac{\sqrt{15}a}{5}\).

Vậy khoảng cách từ điểm A đến mặt phẳng SBD bằng \frac{\sqrt{15}a}{5}\(\frac{\sqrt{15}a}{5}\).

C. Bài tập trắc nghiệm áp dụng tính khoảng cách từ điểm đến mặt phẳng 

Câu 1: Khối tứ diện ABCD có AD vuông góc với mặt phẳng (ABC).AC = 4,AD = 3cm,AB = 6cm\((ABC).AC = 4,AD = 3cm,AB = 6cm\), BC = 5cm\(BC = 5cm\). Khoảng cách từ B đến mặt phẳng (ACD)\((ACD)\) là:

A. \frac{15\sqrt{7}}{4}cm\(\frac{15\sqrt{7}}{4}cm\)                  B. \frac{15\sqrt{7}}{8}cm\(\frac{15\sqrt{7}}{8}cm\)                  C. 3 cm                 D. \frac{3\sqrt{17}}{2}cm\(\frac{3\sqrt{17}}{2}cm\)

Câu 2: Khối tứ diện ABCD có AD vuông góc với mặt phẳng (ABC).AC = 4,AD = 3cm\((ABC).AC = 4,AD = 3cm\), AB = 6cm,BC = 5cm\(AB = 6cm,BC = 5cm\). Khoảng cách từ A đến mặt phẳng (BCD)\((BCD)\) là:

A. \frac{3\sqrt{77}}{11}cm\(\frac{3\sqrt{77}}{11}cm\)     B. \frac{\sqrt{77}}{11}cm\(\frac{\sqrt{77}}{11}cm\)               C. \frac{2\sqrt{77}}{11}cm\(\frac{2\sqrt{77}}{11}cm\)                    D. 3 cm

Đáp án bài tập trắc nghiệm

Câu 1.

Hình vẽ minh họa:

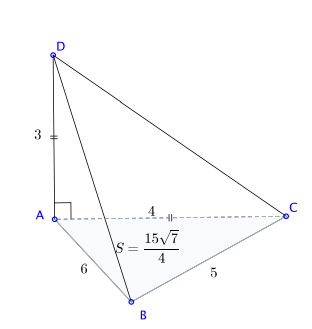
Tính được S_{ABC} = \frac{15\sqrt{7}}{4}\(S_{ABC} = \frac{15\sqrt{7}}{4}\).

Khoảng cách từ B đến (ACD)\((ACD)\) sẽ là đường cao hạ từ B của tam giác ABC.

Ta có: h_{B} = \frac{2S_{ABC}}{AC} = \frac{15\sqrt{7}}{8}\(h_{B} = \frac{2S_{ABC}}{AC} = \frac{15\sqrt{7}}{8}\).

Câu 2. 

Tính được S_{ABC} = \frac{15\sqrt{7}}{4}\(S_{ABC} = \frac{15\sqrt{7}}{4}\). Đường cao hạ từ A của tam giác ABC là:

h_{A} = \frac{2S_{ABC}}{BC} = \frac{3\sqrt{7}}{2}.\(h_{A} = \frac{2S_{ABC}}{BC} = \frac{3\sqrt{7}}{2}.\)

Khi đó gọi d là khoảng cách từ A đến mặt phẳng (BCD)\((BCD)\), ta có \frac{1}{d^{2}} = \frac{1}{h_{A}^{2}} + \frac{1}{AD^{2}} = \frac{11}{63}\(\frac{1}{d^{2}} = \frac{1}{h_{A}^{2}} + \frac{1}{AD^{2}} = \frac{11}{63}\). Suy ra d = \frac{3\sqrt{77}}{11}\(d = \frac{3\sqrt{77}}{11}\).

D. Bài tập tính khoảng cách giữa hai đường thẳng chéo nhau 

Bài toán 1. Cho hình chóp S.ABC\(S.ABC\) có đáy ABC là tam giác vuông tại A, cạnh AB = 2a,AC = a\(AB = 2a,AC = a\). Hình chiếu của S\(S\) lên mặt phẳng (ABC)\((ABC)\) là trung điểm M\(M\) của AB\(AB\). Góc giữa SC\(SC\) và đáy (ABC)\((ABC)\) bằng 60^{\circ}\(60^{\circ}\). Tính khoảng cách giữa AB và SC.

Hướng dẫn giải 

Hình vẽ minh họa:

Dựng hình bình hành ABCD như hình vẽ. Khoảng cách AB và SC đưa về được khoảng cách từ M đến (SCD).

Ta xét khối chóp S.MCD.

Tính được, MC = a\sqrt{2},SM =MC\tan60^{\circ} = a\sqrt{6}\(MC = a\sqrt{2},SM =MC\tan60^{\circ} = a\sqrt{6}\); gọi h_{M}\(h_{M}\) lả đường cao từ M của tam giác MCD, h_{M} = AC = a\(h_{M} = AC = a\).

Gọi tiếp d = d\lbrack M,(SCD)\rbrack\(d = d\lbrack M,(SCD)\rbrack\), ta có:

\frac{1}{d^{2}} = \frac{1}{h_{M}^{2}} +\frac{1}{SM^{2}} = \frac{1}{a^{2}} + \frac{1}{6a^{2}} =\frac{7}{6a^{2}}\(\frac{1}{d^{2}} = \frac{1}{h_{M}^{2}} +\frac{1}{SM^{2}} = \frac{1}{a^{2}} + \frac{1}{6a^{2}} =\frac{7}{6a^{2}}\)

Hay d = \frac{a\sqrt{42}}{7}\(d = \frac{a\sqrt{42}}{7}\).

Vậy khoảng cách giữa AB và SC bằng \frac{a\sqrt{42}}{7}\(\frac{a\sqrt{42}}{7}\).

Nhận xét. Do tính đặc biệt của hình trên, ta không cần tính diện tích tam giác MCD. Tuy nhiên trong trường hợp tổng quát, việc tính diện tích MCD và suy ra đường cao h_{M}\(h_{M}\) sẽ là cần thiết để tính nhanh khoảng cách. Bạn đọc vui lòng thực hành lại phương pháp Herong tính diện tích tam giác MCD để kiểm tra lại đáp án.

---------------------------------------------------------------

Bài viết Công thức tính nhanh khoảng cách (Tập 2) tiếp nối nội dung ở tập trước, mang đến những kỹ thuật mở rộng và bài tập ứng dụng nâng cao giúp học sinh rèn luyện tư duy không gian và tăng tốc độ giải bài. Đây là tài liệu ôn thi Toán 12 quan trọng, hỗ trợ học sinh nắm chắc các công thức tính khoảng cách giữa điểm, đường thẳng và mặt phẳng, từ đó xử lý linh hoạt các câu hỏi vận dụng cao trong đề thi THPT Quốc gia.

Với cách trình bày logic, công thức tổng hợp khoa học và ví dụ minh họa sát thực tế, tài liệu này giúp bạn tối ưu chiến lược làm bài thi trắc nghiệm Toán, củng cố kiến thức hình học không gian và đạt hiệu quả học tập tốt nhất.

Tải về Chọn file muốn tải về:

Công thức tính nhanh khoảng cách (Tập 2)

333 KB Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này! Đóng 79.000 / tháng Mua ngay Đặc quyền các gói Thành viên PRO Phổ biến nhất PRO+ Tải tài liệu Cao cấp 1 Lớp 30 lượt tải tài liệu Xem nội dung bài viết Trải nghiệm Không quảng cáo Làm bài trắc nghiệm không giới hạn Tìm hiểu thêm Mua cả năm Tiết kiệm tới 48%
  • Chia sẻ bởi: Ma Kết
1 6.453 Bài viết đã được lưu Bài trước Mục lục Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi Tìm bài trong mục này

  • A. CHUYÊN ĐỀ TRỌNG TÂM

    • Chuyên đề: Toán thực tế
      • Bài toán tối ưu diện tích
      • Bài toán thực tế về tối ưu chi phí
      • Bài toán Thực tế tối ưu diện tích và thể tích
      • Các bài toán tối ưu kinh tế
      • Bài toán thực tế tối ưu Quãng đường
    • Chuyên đề: Tính đơn điệu của hàm số
      • Tìm khoảng đơn điệu của hàm số y = f(x)
      • Tìm các khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị hàm số
      • Bài tập Tìm khoảng đơn điệu của hàm số cho bởi công thức
      • Bài tập Tìm khoảng đơn điệu của hàm số biết bảng biến thiên, đồ thị hàm số - Có đáp án
      • Tìm tham số m để hàm số đồng biến nghịch biến trên khoảng
      • Bài tập Tìm m để hàm số đồng biến nghịch biến trên khoảng
      • CASIO Tìm nhanh khoảng đơn điệu của hàm số
      • Chuyên đề Xét sự đồng biến, nghịch biến của hàm hợp, hàm ẩn
    • Chuyên đề: Cực trị của hàm số
      • Tìm cực trị của hàm số
      • Bài tập Tìm cực trị của hàm số cho bởi công thức
      • Tìm cực trị của hàm số khi biết bảng biến thiên, đồ thị hàm số
      • Bài tập Tìm cực trị của hàm số khi biết bảng biến thiên, đồ thị hàm số
      • Bài tập Tìm tham số m để hàm số có cực trị
      • Công thức tính nhanh cực trị của hàm số
      • Giải nhanh bài toán cực trị bằng máy tính cầm tay
      • Tính nhanh cực trị hàm trị tuyệt đối
      • Chuyên đề Tìm cực trị của hàm hợp, hàm ẩn
    • Chuyên đề: Đường tiệm cận của đồ thị hàm số
      • Tìm tiệm cận của đồ thị hàm số Toán 12
      • Bài tập Tìm tiệm cận của đồ thị hàm số
      • Tìm m để đồ thị hàm số có n tiệm cận
      • Bài tập Tìm tiệm cận của đồ thị hàm số thông qua bảng biến thiên
      • Bài tập Tiệm cận của đồ thị hàm số có chứa tham số
      • Xác định m để hàm số có tiệm cận đứng – ngang – xiên (Chuyên đề đầy đủ)
    • Chuyên đề: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
      • Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn
      • Bài tập Tìm GTLN, GTNN của hàm số khi biết BBT, đồ thị hàm số
      • Bài tập Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn
      • Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng
      • Bài tập Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng
      • Tìm giá trị lớn nhất nhỏ nhất của hàm chứa dấu giá trị tuyệt đối
      • Cách CASIO tìm nhanh GTLN – GTNN của hàm số
      • Bộ Bài Tập Thực Tế Tìm GTLN – GTNN (Có Đáp Án & Giải Thích Chi Tiết)
    • Chuyên đề. Khảo sát hàm số
      • Nhận dạng đồ thị hàm số Toán 12
      • Bài tập Xác định hàm số thích hợp với đồ thị
      • Bài tập Tương giao đồ thị hàm số cơ bản
      • Tương giao đồ thị hàm số bậc nhất/bậc nhất với đường thẳng
      • Tương giao đồ thị hàm số bậc 3 và đường thẳng
      • Tương giao của đường thẳng với hàm số trùng phương
      • Bài tập Tương giao đồ thị thông qua BBT, đồ thị của hàm số
      • Tìm m để phương trình sau có nghiệm lớp 12
      • Bài tập Tương giao đồ thị hàm số chứa tham số VDC
      • Tìm m để phương trình hàm hợp, hàm ẩn chứa tham số có n nghiệm
    • Chuyên đề. Vectơ và hệ tọa độ trong không gian
      • Bài tập Phân tích Vectơ trong không gian
      • Bài tập Hệ trục tọa độ trong không gian
      • Bài tập Tọa độ của Vectơ trong không gian ứng dụng thực tế
      • Bài tập Biểu diễn tọa độ các phép toán vectơ
      • Bài tập Ứng dụng tọa độ không gian giải bài toán hình học
    • Chuyên đề. Phương trình đường thẳng trong không gian
      • Tổng hợp công thức phương trình đường thẳng trong không gian
      • Bài tập Viết phương trình tham số và chính tắc đường thẳng có đáp án chi tiết
      • Bài tập Toán 12 Vị trí tương đối hai đường thẳng trong không gian (Đáp án cụ thể)
      • Bài tập Toán 12 Tìm hình chiếu của điểm lên đường thẳng và mặt phẳng có đáp án
      • Cách tính khoảng cách từ điểm đến đường thẳng
      • Cách tính khoảng cách giữa hai đường thẳng
    • Chuyên đề. Phương trình mặt phẳng trong không gian
      • Cách viết phương trình mặt phẳng trong không gian Oxyz
      • Tổng hợp công thức phương trình mặt phẳng trong không gian
    • Chuyên đề. Phương trình mặt cầu trong không gian
      • Viết phương trình mặt cầu
      • Sự tương giao và tiếp xúc của mặt cầu với mặt phẳng, đường thẳng
    • Chuyên đề. Nguyên hàm - Tích phân
      • Lý Thuyết Và Bài Tập Nguyên Hàm
      • Bảng Nguyên Hàm Đầy Đủ Nhất
      • Tích phân là gì? Khái niệm và các tính chất tích phân dễ hiểu nhất
      • Bài tập Tính tích phân I
      • Cách bấm máy tính tìm nguyên hàm F(x) của hàm số f(x)
      • Bài tập Tính Nguyên hàm Toán 12 Lời giải chi tiết từng bước
      • Chuyên đề Nguyên hàm hàm lượng giác Toán 12 Có hướng dẫn giải chi tiết
      • Ứng dụng hình học của tích phân: Tính diện tích, thể tích và chiều dài cung
      • Bài tập Ứng dụng hình học tích phân tính diện tích hình phẳng
      • Bài tập Ứng dụng hình học Tích phân tính thể tích
      • Cách dùng Casio giải bài toán tích phân thực tế nhanh và chính xác
      • Bài tập Tính tích phân có điều kiện
      • Tích phân hàm phân thức hữu tỉ: Phương pháp giải và ví dụ chi tiết
      • Bài tập Tích phân hàm phân thức
      • Tích phân hàm lượng giác: Phương pháp giải nhanh và ví dụ minh họa dễ hiểu
      • Bài tập Tích phân hàm lượng giác
    • Chuyên đề Thống kê
    • Chuyên đề Xác suất có điều kiện - Xác suất toàn phần
      • Cách tính xác suất có điều kiện
      • Cách tính Xác suất toàn phần. Công thức Bayes
    • Chuyên đề Hình học thường gặp
      • Hướng dẫn giải chi tiết các bài toán cực trị trong không gian Oxyz
      • Bài toán về quỹ tích - Vị trí tương đối
      • Cách giải nhanh tỉ số thể tích khối chóp tam giác
      • Cách tính Tỉ số thể tích khối chóp có đáy là hình bình hành
      • Cách tính nhanh Tỉ số thể tích khối lăng trụ tam giác
      • Cách tính Tỉ số thể tích khối hộp

  • B. CHUYÊN ĐỀ TRẮC NGHIỆM

    • Trắc nghiệm: Tìm khoảng đơn điệu của hàm số
    • Trắc nghiệm: Tìm khoảng đơn điệu của hàm số biết bảng biến thiên đồ thị hàm số
    • Trắc nghiệm: Tìm m để hàm số đồng biến nghịch biến trên khoảng
    • Trắc nghiệm: Tìm cực trị của hàm số cho bởi công thức
    • Trắc nghiệm: Tìm m để hàm số có cực trị
    • Trắc nghiệm: Tìm cực trị biết bảng biến thiên, đồ thị hàm số
    • Trắc nghiệm: Tìm m để hàm số có tiệm cận
    • Trắc nghiệm: Tìm tiệm cận của hàm số biết bảng biến thiên, đồ thị hàm số
    • Trắc nghiệm: Tìm tiệm cận của hàm số cho bởi công thức
    • Trắc nghiệm: Tìm GTLN, GTNN biết bảng biến thiên đồ thị hàm số
    • Trắc nghiệm: Tìm GTLN, GTNN của hàm số trên đoạn
    • Trắc nghiệm; Tìm GTLN, GTNN của hàm số trên khoảng
    • Trắc nghiệm đúng sai: Tìm giá trị lớn nhất nhỏ nhất của hàm số
    • Trắc nghiệm: Nhận dạng đồ thị hàm số
    • Trắc nghiệm: Tương giao đồ thị thông qua đồ thị, bảng biến thiên
    • Trắc nghiệm: Tương giao đồ thị thông qua hàm số cho trước
    • Trắc nghiệm: Tương giao đồ thị hàm số Vận dụng cao
    • Trắc nghiệm: Ứng dụng đạo hàm giải quyết vấn đề thực tiễn – Có đáp án chi tiết
    • Trắc nghiệm đúng sai: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị (Phần 1)
    • Trắc nghiệm đúng sai: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị (Phần 2)
    • Trắc nghiệm: Phân tích vectơ trong không gian Oxyz
    • Trắc nghiệm: Vecto trong không gian Mức độ VD - VDC
    • Trắc nghiệm: Hệ trục tọa độ trong không gian
    • Trắc nghiệm: Tọa độ của Vectơ trong không gian mức độ VD, VDC
    • Trắc nghiệm: Tích vô hướng của hai vecto trong không gian
    • Trắc nghiệm: Biểu thức tọa độ của các phép toán vectơ
    • Trắc nghiệm: Vị trí tương đối giữa hai đường thẳng
    • Trắc nghiệm: Phương trình đường thẳng (Nhận biết)
    • Trắc nghiệm: Phương trình đường thẳng (Thông hiểu)
    • Trắc nghiệm: Phương trình đường thẳng Mức độ Vận Dụng
    • Trắc nghiệm: Phương trình đường thẳng Vận dụng cao
    • Trắc nghiệm Viết phương trình tham số, phương trình chính tắc của đường thẳng
    • Trắc nghiệm: Tìm hình chiếu của điểm lên đường thẳng, mặt phẳng
    • Trắc nghiệm: Tính khoảng cách trong không gian
    • Trắc nghiệm đúng sai: Phương trình đường thẳng
    • Trắc nghiệm: Tính góc trong không gian
    • Trắc nghiệm: Phương trình mặt phẳng (Nhận biết)
    • Trắc nghiệm: Phương trình mặt phẳng (Thông hiểu Vận Dụng)
    • Trắc nghiệm: Ứng dụng tọa độ không gian giải bài toán hình học
    • Trắc nghiệm: Phương trình mặt cầu cơ bản
    • Trắc nghiệm: Phương trình mặt cầu mức độ Vận dụng
    • Trắc nghiệm: Phương trình mặt cầu mức độ Vận dụng cao
    • Trắc nghiệm: Tìm nguyên hàm của hàm số
    • Trắc nghiệm: Tìm nguyên hàm lượng giác
    • Trắc nghiệm: Sự tương giao tiếp xúc của mặt cầu với mặt phẳng đường thẳng
    • Trắc nghiệm: Tính tích phân I
    • Trắc nghiệm: Tính tích phân có điều kiện
    • Trắc nghiệm: Ứng dụng hình học tích phân
    • Trắc nghiệm đúng sai Ứng dụng tích phân giải bài toán thực tế
    • Trắc nghiệm: Ứng dụng nguyên hàm, tích phân trong thực tế
    • Trắc nghiệm: Tích phân hàm phân thức
    • Trắc nghiệm: Tích phân hàm lượng giác
    • Trắc nghiệm: Ứng dụng tích phân trong các bài toán thực tế
    • Trắc nghiệm: Tính phương sai và độ lệch chuẩn Có đáp án
    • Trắc nghiệm đúng sai: Phương sai và Độ lệch chuẩn
    • Trắc nghiệm: Tính phương sai và độ lệch chuẩn Có đáp án (Tiếp)
    • Trắc nghiệm đúng sai: Khoảng biến thiên và khoảng tứ phân vị
    • Trắc nghiệm Khoảng biến thiên và khoảng tứ phân vị Có đáp án
    • Trắc nghiệm: Khoảng biến thiên và khoảng tứ phân vị Có đáp án (Tiếp)
    • Trắc nghiệm: Xác suất có điều kiện (Nhận biết) – Có đáp án chi tiết
    • Trắc nghiệm: Xác suất có điều kiện (TH - VD) – Có đáp án chi tiết
    • Trắc nghiệm: Xác suất toàn phần Công thức Bayes (Nhận Biết)
    • Trắc nghiệm: Xác suất toàn phần Công thức Bayes (Thông Hiểu)
    • Trắc nghiệm: Xác suất toàn phần Công thức Bayes (VD - VDC)
    • Trắc nghiệm đúng sai: Xác suất có điều kiện có đáp án (Thông hiểu)
    • Trắc nghiệm đúng sai: Xác suất có điều kiện có đáp án (Mức khó)

  • Lớp 12 Lớp 12

  • Toán 12 Toán 12

  • Chuyên đề Toán 12 Chuyên đề Toán 12

  • Thi Tốt Nghiệp THPT Thi Tốt Nghiệp THPT

  • Thi THPT Quốc gia môn Toán Thi THPT Quốc gia môn Toán

  • Đoạn văn NLXH 200 chữ (5-7 dòng) Đoạn văn NLXH 200 chữ (5-7 dòng)

  • Thi THPT Quốc gia môn Văn Thi THPT Quốc gia môn Văn

  • Đề đọc hiểu môn Ngữ Văn Đề đọc hiểu môn Ngữ Văn

  • Thi THPT Quốc gia môn tiếng Anh Thi THPT Quốc gia môn tiếng Anh

  • Thi THPT Quốc gia môn Vật Lý Thi THPT Quốc gia môn Vật Lý

  • Thi THPT Quốc gia môn Hóa học Thi THPT Quốc gia môn Hóa học

  • Thi THPT Quốc gia môn Sinh học Thi THPT Quốc gia môn Sinh học

  • Thi THPT Quốc gia môn Lịch sử Thi THPT Quốc gia môn Lịch sử

  • Thi THPT Quốc gia môn Địa lý Thi THPT Quốc gia môn Địa lý

  • Thi THPT Quốc Gia môn Giáo dục Kinh tế và Pháp luật Thi THPT Quốc Gia môn Giáo dục Kinh tế và Pháp luật

Tham khảo thêm

  • Đề thi thử THPT Quốc gia năm 2017 môn Toán trắc nghiệm - Sở GD&ĐT Vĩnh Phúc

  • Ôn thi Đại học môn Toán - Chuyên đề: Tích phân

  • Đáp án tất cả các môn thi THPT Quốc Gia 2021 đợt 2

  • Tự ôn luyện thi môn Toán

  • Đáp án Toán THPT quốc gia 2021

  • Đề thi thử đánh giá năng lực ĐHQGHN 2016: Tư duy định lượng (môn Toán)

  • Công thức tích phân

  • Cách tìm hình chiếu của điểm lên đường thẳng và mặt phẳng

  • Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

  • 260 bài toán phương trình và hệ phương trình trong ôn thi đại học

🖼️

Thi THPT Quốc gia môn Toán

  • Đề thi thử đánh giá năng lực ĐHQGHN 2016: Tư duy định lượng (môn Toán)

  • Đáp án tất cả các môn thi THPT Quốc Gia 2021 đợt 2

  • Đáp án Toán THPT quốc gia 2021

  • Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

  • Ôn thi Đại học môn Toán - Chuyên đề: Tích phân

  • Công thức tích phân

Xem thêm 🖼️

Gợi ý cho bạn

  • Bộ câu hỏi rung chuông vàng tiếng Anh lớp 4

  • Phương pháp giải hệ phương trình thường gặp trong đề thi đại học

  • 62 bài Toán về số tự nhiên và chữ số - Có đáp án

  • 35 đề và gợi ý tập làm văn hay lớp 4

  • Bài tập tiếng Anh lớp 4 nâng cao có đáp án

  • Đề thi thử đánh giá năng lực ĐHQGHN 2016: Tư duy định lượng (môn Toán)

  • Đáp án Đề thi THPT quốc gia môn Toán năm 2019 chính thức từ Bộ GD&ĐT

  • Đề thi thử ĐHQGHN 2015 phần 1 Tư duy định lượng (môn Toán)

  • Đáp án chính thức của Bộ 2021

  • Ôn thi Đại học môn Toán - Chuyên đề: Số phức

Xem thêm

Từ khóa » Ct Tính Nhanh Khoảng Cách