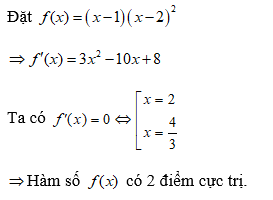Cực Trị Hàm Hợp Chứa Dấu Giá Trị Tuyệt đối Và Các Dạng Bài Tập Minh ...

Home » Toán Học » Cực trị hàm hợp chứa dấu giá trị tuyệt đối và các dạng bài tập minh họa chi tiết Toán Học Cực trị hàm hợp chứa dấu giá trị tuyệt đối và các dạng bài tập minh họa chi tiết admin.ta 16 Tháng Chín, 2021 34 Views 0 SaveSavedRemoved 0

Cực trị hàm hợp chứa dấu giá trị tuyệt đối là bài toán vô cùng thú vị. Nó thường xuất hiện là |f(x)| hoặc f(|x|), nếu không để ý kỹ bạn sẽ nhìn ra 2 cái là như nhau. Nhưng KHÔNG, chúng hoàn toàn khác nhau đấy ?

Hãy theo dõi ngay bài viết dưới đây để cùng xem sự khác nhau giữa chúng là gì cùng chúng tôi nhé !

Tham khảo bài viết khác: 

• Cực trị của hàm số là gì ? Quy tắc và hướng dẫn cách tìm cực trị hàm số đơn giản
• Cực trị hàm hợp là gì ? Hướng dẫn các bước tìm cực trị của hàm hợp chi tiết nhất ?

       Cực trị hàm hợp chứa dấu giá trị tuyệt đối

Tóm tắt nội dung

• 1        Cực trị hàm hợp chứa dấu giá trị tuyệt đối
  • 1.1     1. Cực trị của hàm số y = |f(x)|
  • 1.2     2. Cực trị của hàm số y = f(|x|)
  • 1.3     3. Cực trị của hàm số f (x) = ax^3 + bx^2 + cx + d
• 2        Bài tập tìm cực trị cho các hàm số có dấu giá trị tuyệt đối

    1. Cực trị của hàm số y = |f(x)|

– Để tìm cực trị của hàm số y = |f(x)| ta sẽ lập bảng bảng thiên hoặc vẽ đồ thị hàm số y = | f(x )| từ đồ thị hay bảng biến thiên của hàm y = f(x) .

Chú ý 1: Đồ thị hàm số y = | f(x) | gồm 2 phần:

+ Phần đồ thị y = f(x) nằm trên Ox

+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f(x) nằm dưới Ox

Chú ý 2: Số điểm cực trị của hàm số y = |f(x)| bằng tổng số điểm cực trị của hàm số y = f(x) và số nghiệm bội lẻ của phương trình f(x) = 0

    2. Cực trị của hàm số y = f(|x|)

Để tìm cực trị của hàm số y = f(|x|) ta sẽ lập bảng bảng thiên hoặc vẽ đồ thị hàm số y = f(|x|) từ đồ thị hay bảng biến thiên của hàm y = f(x) .

Tham khảo thêm Tuổi Mão nên mua xe màu gì ? Màu xe thu hút tài lộc, may mắn

Chú ý 1: Đồ thị hàm số y = f(|x|) gồm 2 phần:

+ Phần đồ thị y = f(x) nằm bên phải trục Oy (C1)

+ Phần lấy đối xứng (C1) qua Oy

Chú ý 2: Số điểm cực trị của hàm số y = f(|x|) bằng 2 lần số điểm cực trị dương của hàm số y = f(x) và cộng thêm 1.

    3. Cực trị của hàm số f (x) = ax^3 + bx^2 + cx + d

– Với hàm số f (x) = ax^3 + bx^2 + cx + d có 2 điểm cực trị x1, x2.

==> Khi đó hàm số y = | f(x) | có n điểm cực trị

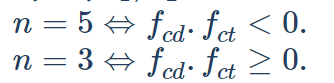
       Bài tập tìm cực trị cho các hàm số có dấu giá trị tuyệt đối

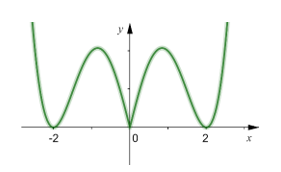
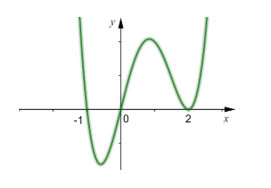
Bài tập 1: Cho hàm số y = f(x) có đồ thị (C) như hình vẽ bên. Hàm số y = f(|x|) có bao nhiêu điểm cực trị ?

– Hướng dẫn giải:

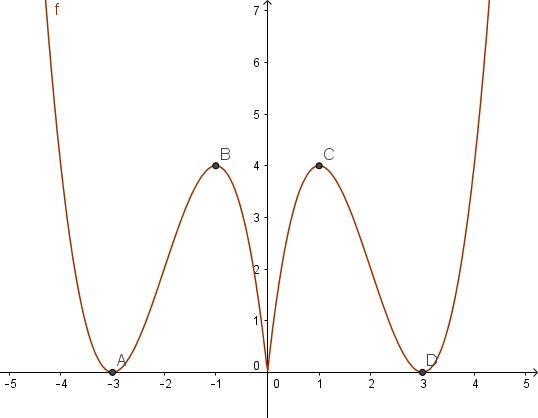
Đồ thị (C’) của hàm số y = f(|x|) được vẽ như sau.

+ Giữ nguyên phần đồ thị của(C) nằm bên phải trục tung ta được (C1)

+ Lấy đối xứng qua trục tung phần đồ thị của (C1) ta được(C2)

+ Khi đó (C’) = (C1)∪(C2) có đồ thị như hình vẽ dưới

Từ đồ thị (C’) ta thấy hàm số y = f(|x|) có 5 điểm cực trị.

Bài tập 2: Cho hàm số y = |(x – 1)(x – 2)^2|. Số điểm cực trị của hàm số là bao nhiêu ?

– Hướng dẫn giải:

=> Mặt khác phương trình f(x) = (x – 1)(x – 2)^2 = 0 có 1 nghiệm đơn x = 1

+> Ta có số điểm cực trị của hàm số y = | (x – 1)(x – 2)^2 | là tổng số điểm cực trị của hàm số f(x) = (x – 1)(x – 2)^2 và số nghiệm bội lẻ của phương trình f(x) = 0.

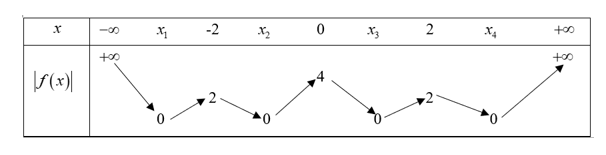
Bài tập 3: Cho hàm số y = f(x) có bảng biến thiên như sau. Đồ thị hàm số y = | f(x) | có bao nhiêu điểm cực trị ?

Tham khảo thêm Tuổi Mão nên mua xe màu gì ? Màu xe thu hút tài lộc, may mắn

– Hướng dẫn giải:

Đồ thị hàm y = |f(x)| gồm 2 phần.

+ Phần đồ thị y = f(x) nằm trên Ox

+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f(x) nằm dưới Ox

Đồ thị hàm số y = f(x) giao với trục Ox tại các điểm có hoành độ x1; x2; x3; x4

Từ đó ta có bảng biến thiên của y = |f(x)|

Từ bảng biến thiên này hàm số y = | f(x) | có 7 điểm cực trị.

Người xem: 554