Cực Trị (không điều Kiện) Của Hàm 2 Biến | Maths 4 Physics & More...
Có thể bạn quan tâm
Ở bài này ta chỉ xét cực trị của hàm hai biến z = f(x,y).
Cho hàm f(x,y) xác định trong miền D và điểm
1. Định nghĩa:
Ta nói là điểm cực tiểu (hoặc cực đại), nếu tồn tại
_lân cận của
sao cho:
( )
Nếu hàm số f đạt cực đại hay cực tiểu (địa phương) tại thì ta nói hàm f đạt cực trị (địa phương) tại
Nhận xét:
– Hàm số đạt cực tiểu (cực đại) tại
nếu:
– Nếu thay đổi dấu khi
thay đổi thì hàm số không đạt cực trị tại
Ví dụ: Bạn hãy xét xem hàm số có đạt cực trị tại M(0;0) hay không?
Xét là 1 điểm trong lân cận của M(0;0). Ta có:
Với
Với
Vậy thay đổi dấu nên hàm f không đạt cực trị tại M0.
2. Quy tắc tìm cực trị không điều kiện:
2.1 Định lý (Điều kiện cần)
Nếu hàm
đạt cực trị (địa phương) tại
và nếu f có các đạo hàm riêng tại
thì:
Chứng minh:
Giả sử hàm f đạt cực đại tại (trường hợp hàm f đạt cực tiểu tại M0 hoàn toàn tương tự ).
Khi đó, xét hàm ta có:
, với x trong 1 khoảng nào đó chứa x0.
Do đó, hàm g(x) đạt cực đại tại x0. Hay:
Mặt khác: . Vậy:
Tương tự, nếu xét hàm ta sẽ có:
Điểm mà tại đó
, được gọi là điểm dừng.
2.2 Định lý (Điều kiện đủ)
Giả sử hàm số
có các đạo hàm riêng đến cấp 2 liên tục trong lân cận của điểm dừng
Đặt:
Khi đó:
a. Nếu
và
(hay C > 0) thì f đạt cực tiểu tại M0.
b. Nếu
và
(hay C < 0) thì f đạt cực đại tại M0.
c. Nếu
thì f không đạt cực trị tại M0.
d. Nếu
ta chưa kết luận và cần phải xét cụ thể bằng cách dựa vào định nghĩa.
Ta công nhận không chứng minh định lý này. Việc chứng minh định lý này, dựa vào việc khai triển Taylor – Maclaurin cho hàm số 2 biến. Khi đó, ta sẽ xét dấu cho vi phân cấp 2 trong khai triển Taylor. Các bạn có thể xem chi tiết chứng minh và công thức Taylor trong giáo trình Toán học Cao cấp (Tập 3) của tác giả Nguyễn Đình Trí. Tuy nhiên, để xem chứng minh 1 cách dễ hiểu nhất, bạn có thể xem trong cuốn Giải tích toán học của tác giả Pixcunop (tập 2).
Ví dụ 1: Tìm cực trị của hàm số:
Ví dụ 2: Tìm cực trị của hàm số:
Đánh giá:
Chia sẻ:
- In
Thảo luận
58 bình luận về “Cực trị (không điều kiện) của hàm 2 biến”
Bình luận về bài viết này Hủy trả lời
Từ khóa » Tìm Cực Trị Của Hàm Số Z = X^3 + Y^3 - 3xy
-
Giải Tích Các Ví Dụ - Mathway
-
Tìm Cực Trị Z=3x2+y3−3xyz=3x^{2}+y^{3}-3xy - Diễn đàn Toán Học
-
[PDF] Cực Trị Hàm Nhiều Biến
-
Tìm điểm Cực Trị Của Hàm 2 Biến \(f(x,y) = {x^3} + {y^3} - 3xy\)
-
Bai5 CUC TRI HAM NHIEU BIEN - Tài Liệu Text - 123doc
-
Câu 1 (3 điểm): Tim Cực Trị Của Hàm Số Z=x^3 +3xy^2 - 15x
-
Tìm điểm Cực Trị Của Hàm 2 Biến \(f(x,y) = {x^3} + {y^3} - 3xy\) | 7scv
-
Tìm điểm Cực Trị Của Hàm 2 Biến (f(x,y) = {x^3} + {y^3} - 3xy)
-
Tìm Cực Trị Của Hàm Số Z(x,y)=x^{3}+y^{3}+3xy-30
-
Bài 4 Tìm Cực Trị Của Các Hàm Số Sa... | Xem Lời Giải Tại QANDA
-
TopList #Tag: Tìm Cực Trị Của Hàm Số Z = X^3 + Y^3 - 3xy - Học Tốt
-
[PDF] Slide Bài Ging Toán A3DH
-
Tìm Cực Trị Hàm 2 Biến - Theza2
-
TO TOÁ ÁN CAO CN CAO CẤ ẤP A3 P A3 Đ ĐẠ ẠI HI HỌ ỌC C
thay oi, thay giup em bai tap: tim cuc tri cua ham so: Z= X^3 =3Xy^2 -15X – 12Y. va Z= X^4+ Y^4 – 2X^2 + 4XY -2Y^2 +1 cam on thay.
ThíchThích
Được đăng bởi sweet_love_1890nd | 12/01/2010, 20:47 Reply to this commentminh dang hoc bang 2 lop ke toan, bo lau qua ko con nho gi, hom nay co bai nay ai tot bung giai ho minh cam on nhieu nha. 1/ Tim cuc tri ham 2 bien sau a/f(x,y)=x2 – 2x – y2 + 8y – 2 b/f(x,y)=-x2 + 2y2 + 6xy – 4x – 10y c/f(x,y)=(x+y-94)(4x+3y) – 6xy
ThíchThích
Được đăng bởi Nguyen Duy Tan | 28/10/2009, 23:07 Reply to this commentMấy bài này là những bài cơ bản mà em, em chỉ cần đọc nội dung bài giảng và các ví dụ minh họa là có thể giải được.
ThíchThích
Được đăng bởi 2Bo02B | 31/10/2009, 23:12 Reply to this commentthưa thầy, thầy cho em hỏi khi D(M)=0 thì mình sẽ giải bằng định nghĩa như thế nào ạh, thầy có thể lấy một bài minh hoạ được không ạh, em cảm ơn thầy!!!
ThíchThích
Được đăng bởi nhungbean | 13/10/2009, 15:29 Reply to this commentEm xem tại đây nhé: https://thunhan.wordpress.com/cung-trao-doi/trao-doi-ve-giai-tich/thao-luan-giai-tich-trng-2/comment-page-4/#comment-3953
ThíchThích
Được đăng bởi 2Bo02B | 14/10/2009, 20:44 Reply to this commentThầy ơi, cho e hỏi chút nhé. Nếu tính cực trị của hàm ko có điều kiện ấy, khi ta tính , ta có thể áp dụng định nghĩa và cho số gia delta X bằng số gia Delta Y, và Delta X bằng trừ Delta Y được không ạ?
, ta có thể áp dụng định nghĩa và cho số gia delta X bằng số gia Delta Y, và Delta X bằng trừ Delta Y được không ạ?
ThíchThích
Được đăng bởi duccuongxc01 | 29/09/2009, 17:13 Reply to this commentTất nhiên, trong trường hợp này phải dùng tới định nghĩa hoặc các công cụ khác. Còn dùng định nghĩa thì phải chứng minh là nó đúng với mọi giá trị của . Như vậy, em có thể cho các trường hợp đặc biệt của
. Như vậy, em có thể cho các trường hợp đặc biệt của  để khẳng định
để khẳng định  thay đổi dấu và từ đó kết luận hàm không đạt cực trị.
thay đổi dấu và từ đó kết luận hàm không đạt cực trị.
ThíchThích
Được đăng bởi 2Bo02B | 30/09/2009, 07:29 Reply to this commentthầy có thể dạy em phần tích phần đường loai 1 được ko ạ em ko thấy có phần tích phần đương loại 1 trong phần dạy của thầy ạ
ThíchThích
Được đăng bởi -T_L- | 22/06/2009, 17:50 Reply to this commentthầy ơi e giải được rùi. e cảm ơn!!!
ThíchThích
Được đăng bởi VuBinh | 16/06/2009, 23:08 Reply to this commentHelp me!!! Tìm cực trị của hàm số z =sinx +cosy +cos( x-y ) voi 0 ≤x,y ≤Π/2
ThíchThích
Được đăng bởi VuBinh | 16/06/2009, 16:10 Reply to this commentBài này làm bình thường, khi tìm điểm dừng chỉ lấy những giá trị x,y nằm trong đoạn [0; pi/2] Giải ra ta tìm được tọa độ điểm dừng là
ThíchThích
Được đăng bởi 2Bo02B | 16/06/2009, 20:00 Reply to this commentBài này em làm mãi ko ra mong thầy cứu em ạ! Tìm cực trị: z = x^3y^2(6-x-y) x,y>=0
ThíchThích
Được đăng bởi Thanh Xuân | 15/06/2009, 19:44 Reply to this commentMặc dù bài này có điều kiện x, y >= 0, nhưng đây không phải là mô hình bài toán cực trị có điều kiện. Vì mô hình bài toán cực trị điều kiện là tìm cực trị hàm z = f(x,y) với (x,y) thỏa mãn phương trình: g(x,y) = 0. Như vậy, bài này em áp dụng phương ph1ap tìm cực trị bình thường, nhưng khi xét điểm dừng, em chỉ xét những điểm thỏa: x, y >=0 thôi. Những điểm còn lại ta không cần quan tâm.
ThíchThích
Được đăng bởi 2Bo02B | 15/06/2009, 20:48 Reply to this commentTính cực trị: z = x^3+3xy^2-15x-12y Mong thầy giúp em ạ!
ThíchThích
Được đăng bởi Thanh Xuân | 15/06/2009, 19:34 Reply to this commentBài này em cứ mạnh dạn làm theo đúng các bước ở phương pháp trên đi. Rồi còn vướng chỗ nào thì Thầy sẽ hướng dẫn.
ThíchThích
Được đăng bởi 2Bo02B | 15/06/2009, 20:42 Reply to this commentbài này cần dựa vào định nghĩa phải ko a.nhưng em ko hiểu cách giải bài này .thầy hướng dẫn cho em .thanks ” khảo sát cực trị của hàm f(x,y)=x^4 + y^4 -x^2-2xy-y^2 “
ThíchThích
Được đăng bởi hmt | 15/06/2009, 16:07 Reply to this commentàh quên bài này có 3 điểm dừng (0,0),(-1,-1);(1,1) tại điểm (1,1)và (-1,-1) hàm đạt cực tiểu theo nghĩ hẹp. thầy hướng dẫn cho em tai điểm (0,0) là được rồi ạ. cám ơn thầy.
ThíchThích
Được đăng bởi hmt | 15/06/2009, 16:17 Reply to this commentEm xem tại đây nhé: https://thunhan.wordpress.com/cung-trao-doi/trao-doi-ve-giai-tich/thao-luan-giai-tich-trng-2/#comment-3958
ThíchThích
Được đăng bởi 2Bo02B | 15/06/2009, 18:43 Reply to this commentcho em hỏi làm bài này như thế nào: tìm cực trị của ham sau z = 5xy + 10/x +20/y em làm z’(x) = 5y -10/x^2 = 0 z’(y) = 5x -20/y^2 = 0 => x=1 y=2 => điểm dừng là M(1,2) A= z”xx(1,2)=20 , B=z”xy(1,2)=5 ,C= Z”yy(1,2)=5 B^2- AC = 25-100 = -75 và A=5 >0 => M(1,2) là cực tiểu
thầy cho em biết là em sai ở bước nào.em cám ơn thầy
ThíchThích
Được đăng bởi Quang | 13/06/2009, 09:27 Reply to this commentKết quả của em nhìn chung là chính xác rồi, chỉ có A = 20 (chứ ko phải A = 5) và không nên ghi là
không nên ghi là  .. Ngoài ra, em nên tính cụ thể
.. Ngoài ra, em nên tính cụ thể  và tính cụ thể giá trị cực tiểu mà hàm số đạt được là bao nhiêu.
và tính cụ thể giá trị cực tiểu mà hàm số đạt được là bao nhiêu.
ThíchThích
Được đăng bởi 2Bo02B | 13/06/2009, 13:11 Reply to this commentthưa thầy cho em hỏi bài nì: tìm cực trị của: Tọa độ điểm dừng là nghiệm hệ:
Tọa độ điểm dừng là nghiệm hệ:  ta tìm được các điểm dừng để đạo hàm riêng kxđ và = 0 là: (0,0) (1,0) (-1,0) (0,1) (0,-1) Xét dz cho từng trường hợp thì ta có dc là: (0,0) là cực đại, còn lại là cực tiểu Mặt khác dễ thấy rằng:
ta tìm được các điểm dừng để đạo hàm riêng kxđ và = 0 là: (0,0) (1,0) (-1,0) (0,1) (0,-1) Xét dz cho từng trường hợp thì ta có dc là: (0,0) là cực đại, còn lại là cực tiểu Mặt khác dễ thấy rằng:  là đồ thị là bán cầu tâm O bán kính r =1, nằm phía trên mp xOy có điểm cực đại (0,0) là hoàn toàn chính xác, nhưng các ngoài các điểm (1,0) (-1,0) (0,1) (0,-1) thì tất cả những điểm trên mp xOy đều là cực tiểu hết . Như vậy, thì đồ thị này có qũy tích điểm cực tiểu là đường tròn tâm O bk r =1 nằm trên xOy. Em thấy hai cách giải trên nó mâu thuẫn với nhau về điểm cực tiểu, em không biết cách nào đúng, thầy giúp em với
là đồ thị là bán cầu tâm O bán kính r =1, nằm phía trên mp xOy có điểm cực đại (0,0) là hoàn toàn chính xác, nhưng các ngoài các điểm (1,0) (-1,0) (0,1) (0,-1) thì tất cả những điểm trên mp xOy đều là cực tiểu hết . Như vậy, thì đồ thị này có qũy tích điểm cực tiểu là đường tròn tâm O bk r =1 nằm trên xOy. Em thấy hai cách giải trên nó mâu thuẫn với nhau về điểm cực tiểu, em không biết cách nào đúng, thầy giúp em với
ThíchThích
Được đăng bởi moneynghia | 29/03/2009, 21:59 Reply to this commentDựa vào kết quả hình học thì chắc chắn đúng rồi, nhưng ở đây 2 đạo hàm riêng còn không xác định với nữa mà. Bài này để đỡ rắc rối ta thấy
nữa mà. Bài này để đỡ rắc rối ta thấy  đạt cực trị khi
đạt cực trị khi  đạt cực trị. Như vậy, hoàn toàn có kết quả như hình học thôi.
đạt cực trị. Như vậy, hoàn toàn có kết quả như hình học thôi.
ThíchThích
Được đăng bởi 2Bo02B | 29/03/2009, 22:37 Reply to this commenttheo em hiểu bài này như vầy: theo đề ta có txđ x^2+y^2<=1 lấy đạo hàm như bạn : x= { 0,1,-1} y={0,1,-1} vậy tất cả các điểm là (0,0) (0,1) (0,-1) (1,0) (-1,0) (1,1) (1,-1) (-1,-1) (-1,1) theo txđ bỏ đi 4 điểm(1,1) (-1,-1) (-1,1) (1,-1) (4 điểm ở cuối) vậy giải sẽ dc kết quả giống bạn.còn phần hình học là sai rồi.vì ở đây chỉ xét trong mặt phẳng Oxy nên chỉ có 4 điểm cực tiểu thui. (em lười viết công thức lém xin lỗi ạ oaoaoa..)
ThíchThích
Được đăng bởi hmt | 15/06/2009, 17:16 Reply to this commentHàm số có thể đạt cực trị tại những điểm đạo hàm riêng cấp 1 triệt tiêu hoặc không tồn tại. Như vậy bài này, đạo hàm không tồn tại tại những điểm thuộc đường tròn tâm O, bán kính R = 1. Xét lại hàm số thì rõ ràng và
và 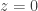 khi
khi  Vậy những điểm nằm trên đường tròn (O;1) đều là những điểm cực tiểu.
Vậy những điểm nằm trên đường tròn (O;1) đều là những điểm cực tiểu.
ThíchThích
Được đăng bởi 2Bo02B | 15/06/2009, 18:45 Reply to this commentthanks thầy nhiều. em biết thiếu nghiệm ở đâu rồi (thi tới nơi mà còn lơ tơ mơ we’ huhu…)
ThíchThích
Được đăng bởi hmt | 15/06/2009, 19:37