Đại Số 8 - Chuyên đề 8 - Bất Phương Trình Bậc Nhất Một ẩn
Có thể bạn quan tâm
Đề thi Toán 8
48 đề thi học sinh giỏi Toán 8 tự luyện
Đề kiểm tra HK1 môn Toán 8 huyện Thạch Thất 2019-2020 có đáp án
Đề kiểm tra giữa HK2 môn Toán 8 THCS Bình Hàn 2018-2019
Đề thi HK2 môn Toán 8 THCS Nam Từ Liêm năm 2018-2019
Đề kiểm tra giữa HK2 môn Toán 8 THPT chuyên Amsterdam 2018-2019
Series hay
- Dạng toán và phương pháp giải Toán lớp 6
- Phiếu bài tập - Toán lớp 6 - THCS Dịch Vọng Hậu
- Bài tập tuần - Toán lớp 7
- Bài tập tuần - Toán lớp 8
- Bài tập tuần - Toán lớp 9
- Ôn tập Hình học 9
- Dạng Toán ôn thi vào 10
- Đề cương ôn thi Toán vào 10 năm học 2017 - 2018
- Vẽ thêm yếu tố phụ để giải bài toán Hình học
- Các phương pháp chứng minh Hình học THCS
- Chuyên đề: Bất đẳng thức THCS
- Đề thi HSG Toán quốc gia
- SGK Toán cấp 2
Từ khóa bài viết
bài tập tuần bất đẳng thức góc phiếu bài tập phân số phương trình quận Hà Đông tam giác THCS Dịch Vọng Hậu THCS Lương Thế Vinh thi vào 10 tuyển sinh vào 10 đa thức đường thẳng đường tròn đề cương đề cương hk1 đề cương toán 7 đề khảo sát đề kiểm tra đề kiểm tra 45 phút đề kiểm tra giữa kì 2 đề kiểm tra hk1 đề kiểm tra hk2 đề kiểm tra học kì đề kiểm tra học kì 1 đề kiểm tra học kì 2 đề kscl đề thi giữa hk2 đề thi giữa kì 2 đề thi hk1 đề thi hk2 đề thi hsg đề thi hsg 6 đề thi hsg 7 đề thi hsg 8 đề thi hsg 9 đề thi học kì 1 đề thi học kì 2 đề thi thử đề thi thử vào 10 đề thi Toán 6 đề thi Toán 8 đề thi toán 9 đề thi vào 10 Toán Cấp 2 11/09/2018 Đại số 8, Toán 8Chuyên đề Toán 8- Đại số 8 – Chuyên đề 1 – Hằng đẳng thức đáng nhớ
- Đại số 8 – Chuyên đề 3 – Phân tích đa thức thành nhân tử
- Đại số 8 – Chuyên đề 4 – Chia đa thức
- Đại số 8 – Chuyên đề 6 – Phương trình bậc nhất một ẩn
- Đại số 8 – Chuyên đề 7 – Giải bài toán bằng cách lập phương trình
- Đại số 8 – Chuyên đề 8 – Bất phương trình bậc nhất một ẩn
- Hình học 8 – Chuyên đề 1 – Hình thang, hình thang cân
- Hình học 8 – Chuyên đề 2 – Đường trung bình của tam giác, hình thang
- Chuyên đề Tứ giác – Hình học 8
- Chuyên đề tam giác đồng dạng – Toán lớp 8
A. Lý thuyết
Mục lục
- 1 1. Bất đẳng thức
- 2 2. Liên hệ giữa thứ tự và phép cộng
- 3 3. Liên hệ giữa thứ tự và phép nhân
- 4 4. Bất phương trình một ẩn
- 4.1 4.1 Nghiệm của bất phương trình
- 4.2 4.2 Tập nghiệm của bất phương trình
- 4.3 4.3 Biểu diễn tập nghiệm
- 5 5. Bất phương trình bậc nhất một ẩn
- 5.1 5.1 Bất phương trình tương đương
- 5.2 5.2 Quy tắc chuyển vế
- 5.3 5.3 Quy tắc nhân
- 6 6. Phương trình chứa dấu giá trị tuyệt đối
1. Bất đẳng thức
| Ta gọi hệ thức $ a<b$ (hay $ a>b;$ $ a\ge b;$ $ a\le b$) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức. |
2. Liên hệ giữa thứ tự và phép cộng
| – Nếu $ a<b$ thì $ a+c<b+c$ – Nếu $ a>b$ thì $ a+c>b+c$
– Nếu $ a\le b$ thì $ a+c\le b+c$ – Nếu $ a\ge b$ thì $ a+c\ge b+c$ Khi cộng cùng một số vào cả hai vế của một bất đẳng thức thì được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho |
Ví dụ: Cho $ a>b\Rightarrow a+3>b+3$
3. Liên hệ giữa thứ tự và phép nhân
| Khi nhân cả hai vế của bất đẳng thức với cùng một số dương thì được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho. Với ba số a, b, c mà $ c>0$ ta có: – Nếu $ a<b$ thì $ ac<bc;$ nếu $ a\le b$ thì $ ac\le bc$ – Nếu $ a>b$ thì $ ac>bc;$ nếu $ a\ge b$ thì $ ac\ge bc$ Khi nhân cả hai vế của bất đẳng thức với cùng một số âm thì được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho. Với ba số a, b, c mà $ c<0$ ta có: – Nếu $ a<b$ thì $ ac>bc;$ nếu $ a\le b$ thì $ ac\ge bc$ – Nếu $ a>b$ thì $ ac<bc;$ nếu $ a\ge b$ thì $ ac\le bc$ |
Ví dụ: $ a>b\Rightarrow a.(-3)<b.\left( {-3} \right)$
4. Bất phương trình một ẩn
4.1 Nghiệm của bất phương trình
| $ x=a$ gọi là nghiệm của bất phương trình nếu ta thay $ x=a$ vào hai vế của bất phương trình thì được một bất đẳng thức đúng |
Ví dụ: x = 3 là nghiệm của bất phương trình $ 2x+3<10$.
$ VT=2.3+3=9;VP=10$. Vì $ 9<10$ nên x = 3 là nghiệm của bất phương trình.
4.2 Tập nghiệm của bất phương trình
| Tập nghiệm của bất phương trình là tập tất cả các giá trị của biến x thỏa mãn bất phương trình. |
4.3 Biểu diễn tập nghiệm
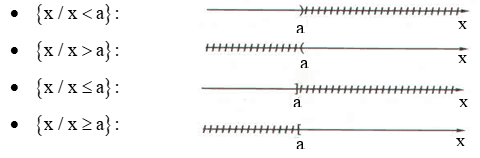
5. Bất phương trình bậc nhất một ẩn
| Hai bất phương trình có cùng tập nghiệm là hai bất phương trình tương đương. |
5.1 Bất phương trình tương đương
Ví dụ: Hai bất phương trình $ 2x+1>0$ và $ x>-\frac{1}{2}$ là hai bất phương trình tương đương.
5.2 Quy tắc chuyển vế
| Khi chuyển vế một hạng tử từ vế này sang vế kia của bất phương trình phải đổi dấu hạng tử đó. |
Ví dụ: $ x+3<0\Leftrightarrow x<-3$
5.3 Quy tắc nhân
| Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:; – Giữ nguyên chiều bất đẳng thức nếu đó là số dương – Đổi chiều bất đẳng thức nếu đó là số âm. |
Ví dụ: $ -x>-3\Leftrightarrow x<3$ (nhân cả hai vế với – 1 thì đổi chiều bất đẳng thức)
6. Phương trình chứa dấu giá trị tuyệt đối
| – Áp dụng định nghĩa giá trị tuyệt đối: – Giải phương trình không có dấu giá trị tuyệt đối – Chọn nghiệm thích hợp trong trường hợp đang xét – Tính chất: $ \left| x \right|\ge 0;$ $ \left| {-x} \right|=\left| x \right|;$ $ {{\left| x \right|}^{2}}={{x}^{2}}$ |
Ví dụ: $ \left| {2x} \right|=x-6$
– Với $ x\ge 0$ ta có: $ \left| {2x} \right|=x-6\Leftrightarrow 2x=x-6\Leftrightarrow x=-6$ (loại)
– Với $ x<0$ ta có: $ \left| {2x} \right|=x-6\Leftrightarrow -2x=x-6\Leftrightarrow x=2$ (loại)
B. Bài tập
Bài toán 1: Cho $ a>b,$ so sánh:
a) $ a-7$ và $ b-7$ c) $ a+30$ và $ b+30$ e) $ a-15$ và $ b-15$
b) $ 6a$ và $ 6b$ d) $ -5a$ và $ -5b$ f) $ a+5$ và $ b+3$
Bài toán 2: So sánh a và b nếu:
a) $ a-7\le b-7$ d) $ 35+a\ge 35+b$ g) $ a+13>b+13$
b) $ -5a<-5b$ e) $ 25+a\ge 25+b$ h) $ 7a-8$ < $ 7b-8$
c) $ a-10\le b-10$ f) $ -14a+7$ >$ -14b+7$ i) $ 2a<2b+1$
Bài toán 3: Cho $ a>0,b>0$ và $ a>b$. Chứng tỏ rằng $ \frac{1}{a}<\frac{1}{b}$.
Bài toán 4: Cho a, b là hai số bất kì, chứng tỏ rằng $ \frac{{{{a}^{2}}+{{b}^{2}}}}{2}\ge ab$.
Bài toán 5: Cho a, b là hai số dương, chứng tỏ rằng $ \frac{a}{b}+\frac{b}{a}\ge 2$.
Bài toán 6: Chứng minh bất đẳng thức:
a) $ {{a}^{2}}+{{b}^{2}}+1\ge ab+a+b$ d) $ {{x}^{2}}+{{y}^{2}}+{{z}^{2}}+3\ge 2\left( {x+y+z} \right)$
b) $ {{a}^{2}}+{{b}^{2}}+{{c}^{2}}\ge a\left( {b+c} \right)$ e) $ \frac{{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}{3}\ge {{\left( {\frac{{x+y+z}}{3}} \right)}^{2}}$
c) $ {{\left( {x+y} \right)}^{2}}\le 2\left( {{{x}^{2}}+{{y}^{2}}} \right)$
Bài toán 7: Chứng minh bất đẳng thức
a) $ \frac{1}{{1.3}}+\frac{1}{{3.5}}+…+\frac{1}{{\left( {2n-1} \right)\left( {2n+1} \right)}}<\frac{1}{2}$
b) $ \frac{1}{{{{1}^{2}}}}+\frac{1}{{{{2}^{2}}}}+…+\frac{1}{{{{n}^{2}}}}<\frac{5}{3}$ với $ n>1$
c) $ \frac{1}{{15}}<\frac{1}{2}.\frac{3}{4}…\frac{{99}}{{100}}<\frac{1}{{10}}$
Bài toán 8: Thử xem $ x=-1$ có là nghiệm của bất phương trình sau không?
a) $ 3x-7>2x+1$ c) $ 7-3x<2-5x$
b) $ -3x-1>x+1$ d) $ 5\left( {x-2} \right)>3x-1$
Bài toán 9: Kiểm tra xem $ x=-2$ có là nghiệm của bất phương trình sau không?
a) $ 3x+5>-9$ c) $ 10-4x>7x-12$
b) $ -5x<2x+3$ d) $ -8x-7<-6x-8$
Bài toán 10: Viết tập nghiệm của bất phương trình sau bằng kí hiệu tập hợp và biểu diễn tập nghiệm đó trên trục số:
a) $ x>4$ c) $ x\ge -1$ e) $ x>7$ g) $ x\ge -2$
b) $ x<-2$ d) $ x\le 3$ f) $ x<0$ h) $ x\le -3$
Bài toán 11: Cho tập hợp $ A=\left\{ {x\in \mathbb{N}/-10\le x\le 10} \right\}.$ Tìm $ x\in A$ là nghiệm của bất phương trình:
a) $ \left| x \right|<4$ b) $ \left| x \right|>7$
c) $ \left| x \right|\le 2$ d) $ \left| x \right|\ge 9$
Bài toán 12: Viết bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau:
a) Tổng của một số nào đó và 11 lớn hơn 17;
b) Hiệu của 15 và một số nào đó nhỏ hơn – 13;
c) Tổng của 3 lần số đó và 7 lớn hơn 8;
d) Hiệu của 10 và 5 lần số đó nhỏ hơn 15;
e) Tổng hai lần số đó và số 3 thì lớn hơn 18;
f) Hiệu của 5 và 3 lần số nào đó nhỏ hơn hoặc bằng 10.
Bài toán 13: Chứng minh các bất phương trình sau:
a) $ {{x}^{2}}+x+1>0$ có nghiệm c) $ \left( {x-1} \right)\left( {x-5} \right)+10<0$ vô nghiệm
b) $ -{{x}^{2}}+3x-3<0$ có nghiệm d) $ {{x}^{2}}+2x<2x$ vô nghiệm
Bài toán 14: Giải các bất phương trình sau:
| 1. $ x+7>-3$ | 16. $ 3x-6>x$ |
| 2. $ x+17<10$ | 17. $ 7x<5x-4$ |
| 3. $ x-4<8$ | 18. $ -5x\le 18+x$ |
| 4. $ x-15>5$ | 19. $ 4{{\left( {x-3} \right)}^{3}}-{{\left( {2x-1} \right)}^{2}}\ge 12x$ |
| 5. $ 5x+18>0$ | 20. $ 2x-x\left( {3x+1} \right)<15-3x\left( {x+2} \right)$ |
| 6. $ 3x-7\le 0$ | 21. $ 3x-5>2\left( {x-1} \right)+x$ |
| 7. $ 9-2x<0$ | 22. $ {{\left( {x+2} \right)}^{2}}-{{\left( {x-2} \right)}^{2}}>8x-2$ |
| 8. $ -11-3x\ge 0$ | 23. $ 1+x-\frac{{x-3}}{4}>\frac{{x+1}}{4}-\frac{{x-2}}{3}$ |
| 9. $ -3x>-4x+7$ | 24. $ 2{{x}^{2}}+2x+1-\frac{{15\left( {x-1} \right)}}{2}\ge 2x\left( {x+1} \right)$ |
| 10. $ 4x+2<3x+3$ | 25. $ 3\left( {4x+1} \right)-2\left( {5x+2} \right)>8x-2$ |
| 11. $ 5x<4x+4$ | 26. $ 4{{x}^{2}}-19×5-{{\left( {2x-3} \right)}^{2}}>0$ |
| 12. $ -6x-3>-7x+9$ | 27. $ 2{{x}^{3}}>x+1$ |
| 13. $ 5x<15$ | 28. $ 5+\frac{{x+4}}{5}<x-\frac{{x-2}}{2}+\frac{{x+3}}{3}$ |
| 14. $ -6x+18\ge 0$ | 29. $ x+1-\frac{{x-1}}{3}<\frac{{2x+3}}{2}+\frac{x}{3}+5$ |
| 15. $ -0,8x+32<0$ | 30. $ \frac{{{{{\left( {3x-2} \right)}}^{2}}}}{3}-\frac{{{{{\left( {2x-1} \right)}}^{2}}}}{3}\le x\left( {x+1} \right)$ |
Bài toán 15: Giải các bất phương trình sau (a là số cho trước):
a) $ 2x-3a\ge 0$
b) $ a+1-5x\ge 0$
c) $ \left( {a-1} \right)x+2a+1>0$ với $ a>1$
d) $ \left( {2a+1} \right)x-1-a\ge 0$ với $ a<-\frac{1}{2}$
e) $ \left( {{{a}^{2}}+1} \right)x+a-1<0$
f) $ \left( {{{a}^{2}}-2a+2} \right)x\ge 2a+3$
Bài toán 16: Viết thành bất phương trình và giải:
a) Tìm x sao cho biểu thức $ x-3,5$ nhận giá trị âm;
b) Tìm x sao cho biểu thức $ x+11$ nhận giá trị dương;
c) Tìm x sao cho biểu thức $ 3x-5$ lớn hơn 4;
d) Tìm x sao cho giá trị của biểu thức $ 5x-4$ lớn hơn giá trị của biểu thức $ 3x-12.$
Bài toán 17: Tìm các giá trị của x thỏa mãn cả hai bất phương trình:
$ \frac{{{{{\left( {x-3} \right)}}^{2}}}}{3}-\frac{{{{{\left( {2x-1} \right)}}^{2}}}}{{12}}\le x$ (1)
$ 2+\frac{{3\left( {x+1} \right)}}{3}<3-\frac{{x-1}}{4}$ (2)
Bài toán 18: Tìm các số nguyên x thỏa mãn cả hai bất phương trình:
$ \frac{{x-5}}{4}-\frac{{2x-1}}{2}\le 3$ (1)
$ \frac{{2x-3}}{3}<\frac{{x+1}}{2}$ (2)
Bài toán 19: Tìm giá trị của m để mỗi bất phương trình sau có nghiệm dương:
a) $ \frac{{x+1}}{{1-m}}+\frac{{x-1}}{{1+m}}=\frac{{x+m}}{{1+m}}+\frac{{2\left( {x-m} \right)}}{{1-m}}$
b) $ 4-m=\frac{2}{{x+1}}$
Bài toán 20: Tìm giá trị của m để mỗi bất phương trình sau có nghiệm âm
a) $ 0,5\left( {5x-1} \right)=4,5-2m\left( {x-2} \right)$
b) $ \frac{{3mx+12m+5}}{{9{{m}^{2}}-1}}=\frac{{2x-3}}{{3m+1}}-\frac{{3x-4m}}{{1-3m}}$
Bài toán 21: Tìm các giá trị nguyên của x để biểu thức $ A=\frac{{x-1}}{5}-\frac{{x-2}}{3}$ có giá trị lớn hơn 1 nhứng nhỏ hơn 3.
Bài toán 22: Với giá trị nào của a thì phương trình $ \frac{{a+1}}{{x-1}}=1-a$ có nghiệm dương nhỏ hơn 1.
Bài toán 23: Xác định m để bất phương trình $ \left( {{{m}^{2}}-4m+3} \right)x+m-{{m}^{2}}<0$ nghiệm đúng với mọi x.
Bài toán 24: Giải phương trình
| 1. $ \left| {2x-5} \right|=2-x$ | 11. $ \left| {3-2x} \right|=3x-7$ |
| 2. $ \left| {2x-7} \right|=17-x$ | 12. $ \left| {\frac{x}{2}-\frac{5}{4}} \right|=x-1$ |
| 3. $ \left| {3x-2} \right|=1-x$ | 13. $ \left| {x+2} \right|=2\left( {3-x} \right)$ |
| 4. $ \left| {2x-3} \right|=x$ | 14. $ \left| {3x} \right|-x-4=0$ |
| 5. $ \left| {3x} \right|=x+7$ | 15. $ \left| {6-x} \right|=2x-3$ |
| 6. $ \left| {5x} \right|=3x+8$ | 16. $ 9-\left| {-5x} \right|+2x=0$ |
| 7. $ \left| {-4,5x} \right|=6+2,5x$ | 17. $ {{\left( {x+1} \right)}^{2}}+\left| {x+10} \right|-{{x}^{2}}-12=0$ |
| 8. $ \left| {-4x} \right|=-2x+11$ | 18. $ \left| {4-x} \right|+{{x}^{2}}-\left( {5+x} \right)x=0$ |
| 9. $ \left| {x-9} \right|=2x+5$ | 19. $ 10x-10+\left| {3x-5} \right|-5\left( {2x-3} \right)=0$ |
| 10. $ \left| {3x-1} \right|=4x+1$ | 20. $ {{\left( {x-2} \right)}^{2}}+\left| {x-5} \right|-{{x}^{2}}-14=0$ |
Bài toán 25: Giải phương trình
a) $ \frac{{\left| x \right|-1}}{4}-\frac{1}{8}\left( {\frac{{\left| x \right|-5}}{4}-\frac{{14-2\left| x \right|}}{5}} \right)=\frac{{\left| x \right|-9}}{2}-\frac{7}{8}$
b) $ \frac{{7x+5}}{5}-x=\frac{{\left| {3x-5} \right|}}{2}$
c) $ x-\frac{{\left| {3x-2} \right|}}{5}=3-\frac{{2x-5}}{3}$
Bài toán 26: Giải phương trình
a) $ {{x}^{2}}-\left| x \right|=6$ e) $ \left| {x+1} \right|-\left| {2-x} \right|=0$
b) $ \left| {{{x}^{2}}-4} \right|={{x}^{2}}-4$ f) $ \left| x \right|-\left| {x-2} \right|=2$
c) $ \left| {2x-{{x}^{2}}-1} \right|=2x-{{x}^{2}}-1$ g) $ \left| {x-1} \right|+\left| {x-2} \right|=1$
d) $ \left| {{{x}^{2}}-3x+3} \right|=3x-{{x}^{2}}-1$ h) $ \left| {x-2} \right|+\left| {x-3} \right|+\left| {2x-8} \right|=9$
Bài toán 27: Giải phương trình
a) $ 3x\left| {x+1} \right|-2x\left| {x+2} \right|=12$
b) $ \frac{{{{x}^{2}}-4-\left| {x-2} \right|}}{2}=x\left( {x+1} \right)$
c) $ \frac{{{{x}^{3}}+{{x}^{2}}-x}}{{x\left| {x-2} \right|}}=1$
d) $ \frac{7}{{8x}}+\frac{{5-x}}{{4{{x}^{2}}-8x}}=\frac{{x-1}}{{2x\left( {x-2} \right)}}+\frac{1}{{8x-16}}$
e) $ \frac{{x+2}}{{{{x}^{2}}+2x+4}}-\frac{{x-2}}{{{{x}^{2}}-2x+4}}=\frac{6}{{x\left( {{{x}^{4}}+4{{x}^{2}}+16} \right)}}$
f) $ \frac{{{{x}^{2}}-x}}{{x+3}}-\frac{{{{x}^{2}}}}{{x-3}}=\frac{{7{{x}^{2}}-3x}}{{9-{{x}^{2}}}}$
Bài toán 28: Giải bất phương trình
a) $ \left| {2x+5} \right|\le \left| {7-4x} \right|$
b) $ \left| {\frac{{2-3\left| x \right|}}{{1+x}}} \right|\le 1$
c) $ \frac{{\left| {{{x}^{2}}-4x} \right|+3}}{{{{x}^{2}}+\left| {x-5} \right|}}\ge 1$
d) $ \frac{9}{{\left| {x-5} \right|-3}}\ge \left| {x-3} \right|$
e) $ \left| {2x-1} \right|\ge x-1$
f) $ \left| {2x+5} \right|>\left| {7-4x} \right|$
Bài toán 29: Giải và biện luận bất phương trình
a) $ -1\le \frac{{x+m}}{{mx+1}}\le 1$ b) $ \frac{{x-m}}{{x+1}}=\frac{{x-2}}{{x-1}}$ c) $ \frac{{ax-1}}{{x–1}}+\frac{b}{{x+1}}=\frac{{a\left( {{{x}^{2}}+1} \right)}}{{{{x}^{2}}-1}}$
Bài toán 30: Chứng minh các bất đẳng thức
a) $ {{a}^{2}}+{{b}^{2}}\ge \frac{1}{2}$ với $ a+b=1;$
b) $ {{a}^{2}}+{{b}^{2}}+{{c}^{2}}\ge \frac{1}{3}$ với $ a+b+c=1$
c) $ {{a}_{1}}^{2}+{{a}_{2}}^{2}+…+{{a}_{n}}^{2}\ge \frac{1}{n}$ với $ {{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}=1$
Bài toán 31: Cho biểu thức
$ M=\left[ {\frac{{3\left( {x+2} \right)}}{{2\left( {{{x}^{3}}+{{x}^{2}}+x+1} \right)}}+\frac{{2{{x}^{2}}-x-10}}{{2\left( {{{x}^{3}}+{{x}^{2}}+x+1} \right)}}} \right]:\left[ {\frac{5}{{{{x}^{2}}+1}}+\frac{3}{{2\left( {x+1} \right)}}-\frac{3}{{2\left( {x-1} \right)}}} \right].\frac{2}{{x-1}}$
a) Rút gọn M;
b) Tính giá trị của M biết $ \left| x \right|=\frac{1}{3};$
c) Tìm x biết $ \left| M \right|=2004;$
d) Tìm giá trị của x để $ M>0,$ $ M<0;$
e) Tìm các giá trị nguyên của x để giá trị của biểu thức M là số nguyên.
Bài toán 32: Trong một buổi lao động trồng cây, cô giáo chủ nhiệm đã phân công cho các tổ lần lượt như sau:
Tổ I trồng 20 cây và 4% số cây còn lại.
Tổ II trồng 21 cây và 4% số cây còn lại.
Tổ II trồng 22 cây và 4% số cây còn lại.
Cứ chia như vậy cho đến tổ cuối cùng thì vừa hết số cây và số cây mỗi tổ trồng đều bằng nhau. Hỏi lớp đó có bao nhiêu tổ, số cây lớp trồng được là bao nhiêu?
Bài toán 33: Trong một lớp có 14 học sinh giỏi Toán, 13 học sinh giỏi Văn. Số học sinh vừa giỏi Toán, vừa giỏi Văn bằng một nửa số học sinh không giỏi Toán mà cũng không giỏi Văn. Hỏi có bao nhiêu học sinh vừa giỏi Toán, vừa giỏi Văn, biết rằng số học sinh của lớp đó là 35.
Series Navigation<< Đại số 8 – Chuyên đề 7 – Giải bài toán bằng cách lập phương trìnhHình học 8 – Chuyên đề 1 – Hình thang, hình thang cân >>Bài viết liên quan
- Lý thuyết bất phương trình bậc nhất một ẩn cần ghi nhớ – Toán lớp 8
- Bất phương trình bậc nhất một ẩn
- Bất phương trình một ẩn, bất phương trình tương đương
Trả lời Hủy
Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *
Bình luận
Tên *
Email *
Trang web
Kho tài liệu PDF
Đề thi vào lớp 10
Kho tài liệu PDF
Bài viết mới
- 11 dạng toán về phân số – Số học 6
- Các dạng toán Tính tổng dãy số lũy thừa có quy luật – Số học 6
- Tập hợp và bài tập áp dụng – Số học 6
- Đề kiểm tra 15 phút – Đề 2 – Tính chất cơ bản của phân số
- Đề kiểm tra 15 phút – Đề 1 – Tính chất cơ bản của phân số
Nhiều người đọc
Sorry. No data so far.
Toán THCS
| Toán 6 | Sách Toán 6 |
| Toán 7 | Sách Toán 7 |
| Toán 8 | Sách Toán 8 |
| Toán 9 | Sách Toán 9 |
Lưu trữ
Lưu trữ Chọn tháng Tháng Tư 2020 (57) Tháng Ba 2020 (8) Tháng Hai 2020 (5) Tháng Một 2020 (20) Tháng Mười Hai 2019 (93) Tháng Mười Một 2019 (12) Tháng Mười 2019 (36) Tháng Chín 2019 (11) Tháng Tám 2019 (31) Tháng Bảy 2019 (1) Tháng Sáu 2019 (36) Tháng Năm 2019 (71) Tháng Tư 2019 (70) Tháng Ba 2019 (49) Tháng Hai 2019 (11) Tháng Một 2019 (16) Tháng Mười Hai 2018 (95) Tháng Mười Một 2018 (44) Tháng Mười 2018 (62) Tháng Chín 2018 (140) Tháng Sáu 2018 (34) Tháng Năm 2018 (10) Tháng Tư 2018 (23) Tháng Ba 2018 (13) Tháng Hai 2018 (34) Tháng Một 2018 (64) Tháng Mười Hai 2017 (222) Tháng Mười Một 2017 (103) Tháng Mười 2017 (70) Tháng Chín 2017 (26) Tháng Tám 2017 (35) Tháng Bảy 2017 (265) Tháng Sáu 2017 (28) Toán THCS © 2012 Liên hệ tài liệu đại họcTừ khóa » Bài Tập Bất Phương Trình Bậc Nhất Một ẩn
-
Giải Bất Phương Trình Bậc Nhất Một ẩn
-
15 Bài Tập Bất Phương Trình Bậc Nhất Một ẩn Có đáp án | Toán Lớp 8
-
Chuyên đề Bất Phương Trình Bậc Nhất Một ẩn - Toán THCS
-
Giải Bất Phương Trình Bậc Nhất Một Ẩn Lớp 8 - Kiến Guru
-
Giải Toán 8 Bài 4. Bất Phương Trình Bậc Nhất Một ẩn
-
Chuyên đề Bất Phương Trình Bậc Nhất Một ẩn
-
Bất Phương Trình Bậc Nhất Một ẩn - Toán 8
-
Chuyên đề: Bất Phương Trình Bậc Nhất Một ẩn - Toán Lớp 8
-
Bất Phương Trình Bậc Nhất Một ẩn Là Gì? - TopLoigiai
-
Toán Lớp 8 | Bất Phương Trình Bậc Nhất Một ẩn | Học Thật Tốt
-
Bài Tập Về Bất Phương Trình Bậc Nhất Một ẩn | Chuyên đề Toán 8
-
Bài Tập Bất Phương Trình Bậc Nhất Một ẩn Chọn Lọc, Có đáp án
-
Bất Phương Trình Bậc Nhất Một ẩn – Lý Thuyết & Bài Tập - I Toán - Itoan
-
Cách Giải Bài Toán Dạng: Giải Bất Phương Trình Bậc Nhất Một ẩn