Dạng 5: Bài Toán Cực Trị

* Thay đổi L để UL lớn nhất

Ta có: \(U_L = I.Z_L = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_L = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{L}^{2}}}}\) \(\Rightarrow U_L = \frac{U}{\sqrt{\frac{R^2+Z_{L}^{2}-2Z_LZ_C+Z_{C}^{2}}{Z_{L}^{2}}}} = \frac{U}{\sqrt{\frac{R^2+Z_{C}^{2}}{Z_{L}^{2}}-2\frac{Z_C}{Z_L}+1}} = \frac{U}{\sqrt{y}}\) Với \(\left\{\begin{matrix} y=(R^2 + Z_{C}^{2}).x^2 - 2Z_C.x + 1\\ x=\frac{1}{Z_L} \hspace{4,2cm} \end{matrix}\right.\) \(\left ( \begin{matrix} y = ax^2 + bx+ c\\ \left\{\begin{matrix} a = R^2 + Z_{C}^{2}\\ b=-2Z_C \ \ \ \ \\ c=1 \ \ \ \ \ \ \ \ \ \ \end{matrix}\right. \end{matrix} \right )\) Do U không đổi \(\Rightarrow (U_L)_{max} \Leftrightarrow y_{min} \Rightarrow x = -\frac{b}{2a}\) \(\Rightarrow \frac{1}{Z_L}=\frac{Z_C}{R^2 + Z_{C}^{2}} \Rightarrow Z_L=\frac{R^2 + Z_{C}^{2}}{Z_C} \Rightarrow U_{L\ max} = \frac{U}{R}\sqrt{R^2 + Z_{C}^{2}}\) * Giản đồ vecto 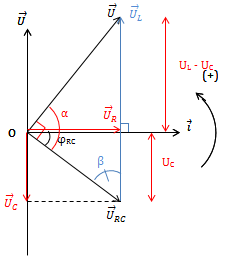Ta có: \(\frac{U_L}{\sin \alpha } = \frac{U}{\sin \beta } \Rightarrow U_L = \frac{U}{\sin \beta }.\sin \alpha\) Do U, \(\beta\) không đổi \(\Rightarrow U_{L\ max} \Leftrightarrow \sin \alpha = 1 \Rightarrow \alpha = \frac{\pi }{2}\) \(\cdot \ \overrightarrow{U}_{RC} \perp \overrightarrow{U} \Rightarrow U_{RC}^{2} = U_C.U_L \Rightarrow Z_{RC}^{2} = Z_C.Z_L \Rightarrow Z_L = \frac{R^2 + Z_{C}^{2}}{Z_C}\) \(\cdot \ U_{RC}.U = U_{R}.U_{L} \Rightarrow U_{L} = \frac{U}{U_R}.U_{RC}\) \(\cdot \ U_{R}^{2}= U_{C}(U_{L}-U_{C})\) \(\cdot \ U^{2}= (U_{L}-U_{C}).U_{L}\) \(U_{L}^{2}= U^2 + U_{RC}^{2}\) \(\Rightarrow U_{L}^{2}= U^2 + U_{R}^{2} + U_{C}^{2}\)

* Thay đổi C để UC lớn nhất Ta có: \(U_C = I.Z_C = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_C = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{C}^{2}}}}\) \(\Rightarrow U_C = \frac{U}{\sqrt{\frac{R^2+Z_{L}^{2}}{Z_{C}^{2}}-2\frac{Z_L}{Z_C}+1}} = \frac{U}{\sqrt{y}}\) Với \(\left\{\begin{matrix} y=(R^2 + Z_{L}^{2}).x^2 - 2Z_L.x + 1 \ \ \ (y = ax^2 + bx + c)\\ x=\frac{1}{Z_C} \hspace{8cm} \end{matrix}\right.\) Do U không đổi \(\Rightarrow U_{c\ max} \Leftrightarrow y_{min} \Rightarrow x = -\frac{b}{2a}\) \(\Rightarrow \frac{1}{Z_C}=\frac{Z_L}{R^2 + Z_{L}^{2}} \Rightarrow Z_C=\frac{R^2 + Z_{L}^{2}}{Z_L} \Rightarrow U_{C\ max} = \frac{U}{R}\sqrt{R^2 + Z_{L}^{2}}\)

* Thay đổi C để UC max (Giản đồ vecto) 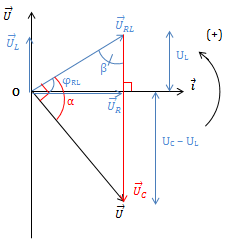Ta có: \(\frac{U_C}{\sin \alpha } = \frac{U}{\sin \beta } \Rightarrow U_C = \frac{U}{\sin \beta }.\sin \alpha\) Do U, \(\beta\) không đổi \(\Rightarrow U_{C\ max} = \frac{U}{\sin \beta }\) khi \(\sin \alpha =1 \Rightarrow \alpha =\frac{\pi}{2}\) \(\cdot \ \overrightarrow{U}_{RL} \perp \overrightarrow{U} \Rightarrow U_{RL}^{2} = U_L.U_C \Rightarrow Z_{RL}^{2} = Z_L.Z_C\) \(\Rightarrow Z_C = \frac{R^2 + Z_{L}^{2}}{Z_L}\) \(\cdot \ U.U_{RL} = U_{R}.U_{C} \Rightarrow U_{C} = \frac{U}{U_{R}}.U_{RL} = \frac{U}{R}.\frac{U_{RL}}{I}\) \(\Rightarrow U_{C} = \frac{U}{R}.Z_{RL}=\frac{U}{R}\sqrt{R^2 + Z_{L}^{2}}\) * Chú ý: (1) Thay đổi C thấy có 2 giá trị C1, C2 thì UC1 = UC2; khi C = C0 thì UC max: \(\Rightarrow x_1 + x_2 = -\frac{b}{a} = 2x_0 \Rightarrow \frac{1}{Z_{C_1}} + \frac{1}{Z_{C_2}} = \frac{2}{Z_{C_0}}\) ⇒ C1 + C2 = 2C0 (2) Thay đổi C để: \(\\ + \ U_{R \ max} = U\\ + \ U_{L \ max} = \frac{U}{R}.Z_L\\ + \ U_{RL \ max} = \frac{U}{R}.Z_{RL}\) ⇒ Cộng hưởng điện.

* Thay đổi \(\omega\) để UL max Ta có: \(U_L = I.Z_L = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_L = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{L}^{2}}}}\) \(\Rightarrow U_L = \frac{U}{\sqrt{\frac{R^2}{Z_{L}^{2}}+\left ( 1-\frac{Z_C}{Z_L} \right )^2}} = \frac{U}{\sqrt{\frac{R^2}{L\omega ^2}+\left ( 1-\frac{1}{LC\omega ^2} \right )^2}}\) \(\Rightarrow U_L = \frac{U}{\sqrt{\frac{R^2}{L^2 \omega ^2}+1-\frac{2}{LC \omega ^2}+\frac{1}{L^2C^2 \omega ^4}}} = \frac{U}{\sqrt{\frac{1}{L^2C^2 \omega ^4}-\left ( \frac{2}{LC}-\frac{R^2}{L^2} \right )\frac{1}{\omega ^2}+1}}\) \(\Rightarrow U_L = \frac{U}{\sqrt{y}}\) với \(\left\{\begin{matrix} y = \frac{1}{L^2C^2}.x^2 - \left ( \frac{2}{LC} - \frac{R^2}{L^2} \right ).x + 1\\ x = \frac{1}{\omega ^2} \hspace{4,6cm} \end{matrix}\right.\) Do U không đổi \(\Rightarrow (U_L)_{max} \Leftrightarrow y_{min} \Leftrightarrow x = -\frac{b}{2a}\) \(\Rightarrow \frac{1}{\omega ^2} = \frac{\frac{2}{LC}-\frac{R^2}{L^2}}{\frac{2}{L^2C^2}} = \left ( \frac{2}{LC}-\frac{R^2}{L^2} \right ).\frac{L^2C^2}{2}\) \(\Rightarrow \frac{1}{\omega ^2} = \frac{2LC - R^2C^2}{2} \Rightarrow \omega _L = \sqrt{\frac{2}{2LC - R^2C^2}}\) \(2LC - R^2C^2 > 0\Leftrightarrow CR^2 < 2L\) * Chú ý: Thay đổi \(\omega\) có 2 giá trị \(\omega _1, \omega _2\) thì \(U_{L_1} = U_{L_2}\); khi \(\omega = \omega _L\) thì UL max \(\Rightarrow x_1 + x_2 = -\frac{b}{a} = 2x_L \Rightarrow \frac{1}{\omega _{1}^{2}} +\frac{1}{\omega _{2}^{2}} = \frac{2}{\omega _{L}^{2}}\)

* Thay đổi \(\omega\) để UC max Ta có: \(U_C = I.Z_C = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_C = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{C}^{2}}}}\) \(\Rightarrow U_C = \frac{U}{\sqrt{\frac{R^2}{Z_{C}^{2}}+\left ( \frac{Z_L}{Z_C}-1 \right )^2}} = \frac{U}{\sqrt{R^2C^2\omega ^2+(LC\omega ^2 - 1)^2}}\) \(\Rightarrow U_C = \frac{U}{\sqrt{R^2C^2\omega ^2 + L^2C^2\omega ^4 - 2LC\omega ^2 + 1}}\) \(= \frac{U}{\sqrt{L^2C^2\omega ^4 - (2LC - R^2C^2)\omega ^2 + 1}} = \frac{U}{\sqrt{y}}\) Với \(\left\{\begin{matrix} y = L^2C^2x^2 - (2LC - R^2C^2)x + 1\\ x = \omega ^2 \hspace{5cm} \end{matrix}\right.\) Do U không đổi \(\Rightarrow U_{C\ max} \Leftrightarrow y_{min} \Rightarrow x = \frac{-b}{2a}\) \(\Rightarrow \omega ^2 = \frac{2LC - R^2C^2}{2L^2C^2} \Rightarrow \omega _C = \frac{1}{LC}.\sqrt{\frac{2LC - R^2C^2}{2}}\) * Chú ý: Thay đổi \(\omega\) có 2 giá trị \(\omega _1, \omega _2\) thì \(U_{C_1} = U_{C_2}\); khi \(\omega = \omega _C\) thì UC max \(\Rightarrow x_1 + x_2 = 2x_C \Rightarrow \omega _{1}^{2} + \omega _{2}^{2} = 2\omega _{C}^{2}\) Nhận xét: \(\cdot \ \omega _{0}^{2} = \frac{1}{LC}\) (CHĐ) \(\cdot \ \omega _{C} = \frac{1}{LC}.\sqrt{\frac{2LC - R^2C^2}{2}}\) \(\cdot \ \omega _{L} = \sqrt{\frac{2}{2LC - R^2C^2}}\) Ta có mối liên hệ \(\Rightarrow \omega _C \omega _L = \omega _{0}^{2}\)

VD1: Đặt điện áp \(u = 200\sqrt{2}\cos 100 \pi t\) (V) vào 2 đầu mạch RLC ghép nối tiếp có L thay đổi được. Thay đổi L để UL max = 250 V thì UR bằng bao nhiêu? Giải: 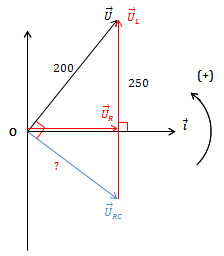\(\cdot \ U_{RC} = \sqrt{U_{L}^{2} - U^2} = \sqrt{250^{2} - 200^2} \Rightarrow U_{RC} = 150 \ V\) \(\cdot \ U_{R} = \frac{U.U_{RC} }{U_L} = \frac{200.150}{250} = 120\ V\)

VD2: Đặt điện áp \(u = 100\sqrt{2}\cos (100 \pi t - \frac{\pi }{3})\) (V) vào 2 đầu mạch gồm \(R = 50\Omega\) nối tiếp cuộn dây chỉ có \(L = \frac{2}{5 \pi }\) (H) và tụ C thay đổi được. Thay đổi C để điện áp hiệu dụng 2 đầu cuộn dây lớn nhất bằng bao nhiêu? Giải: Thay đổi C để \(U_{L\ max} = \frac{U}{R}.Z_L\) Với \(\left\{\begin{matrix} U = 100 \ V \hspace{2,8cm}\\ R = 50\Omega \hspace{3,2cm}\\ Z_L = L \omega =\frac{2 \pi}{5}.100\pi = 40\Omega \end{matrix}\right.\) \(\Rightarrow U_{L\ max} = \frac{100}{50}.40 = 80\ V\)