Đạo Hàm Của Hàm Hợp | Maths 4 Physics & More...
Có thể bạn quan tâm
1. Định nghĩa:
Giả sử phương trình (1) xác định với u, v là hàm số của các biến độc lập x và y:
(2) thì khi đó z được gọi là hàm số hợp của các biến số x và y thông qua 2 biến trung gian u và v.
Như vậy z cũng có thể biểu diễn như hàm 2 biến x, y: (3)
Ví dụ: Cho
Khi đó:
Tình huống:
Nếu ta cần khảo sát đạo hàm của hàm số hợp thì có thể viết hàm số dưới dạng tường minh theo 2 biến x, y. Tuy nhiên, với hàm trên thì việc lấy đạo hàm riêng sẽ rất khó khăn. Hoặc nếu hàm số chưa xác định được công thức, ví dụ:
hoặc
thì làm sao tính được các đạo hàm riêng
2. Định lý: (Tính từ (1), (2) mà không dùng (3)
Cho z = f(u,v) và u, v là các hàm của hai biến u = u(x,y) và v = v(x,y). Cho các hàm z, u, v khả vi tại các điểm tương ứng. Khi đó, z = f(u,v) có các đạo hàm riêng
xác định bởi công thức:
;
3. Quy tắc Xích để xác định công thức tính đạo hàm cho hàm hợp:
 – Dòng 1: Viết hàm cần tính đạo hàm z
– Dòng 1: Viết hàm cần tính đạo hàm z
– Dòng 2: Xác định các biến trung gian có trong hàm z. Ví dụ: (u,v)
– Dòng 3: xác định biến cần lấy đạo hàm. Ví dụ x
– Nối z với các biến trung gian u, v bằng những đoạn kẻ. Mỗi đoạn kẻ tương ứng với phép lấy đạo hàm.
– Nếu u, v là những biến phụ thuộc x thì nối u với x bằng 1 đường kẻ; nối v với x bằng 1 đường kẻ. Các đường kẻ trên chính là các phép toán lấy đạo hàm riêng.
– Tổng hợp tất cả các cách nối được từ z đến x ta sẽ có công thức tính đạo hàm của z theo x.
4. Một số trường hợp tổng quát:
 1. Với z = f(u,v, w) , trong đó u = u(t), v = v(t), w = w(t)
1. Với z = f(u,v, w) , trong đó u = u(t), v = v(t), w = w(t)
Khi đó: z là hàm số hợp của 1 biến số t thông qua 3 biến trug gian u, v, w.
Bấy giờ, đạo hàm của z theo t được xác định
(do z, u, v, w đều là hàm theo 1 biến t nên đạo hàm là đạo hàm thường)
Áp dụng: tính , nếu
, với
Tương tự quy tắc trên, ta có:
Nghĩa là:
Hay:
Ví dụ 1: Tính nếu
với y = f(x).
Trong ví dụ này, ta cần chú ý và phân biệt ý nghĩa của hai ký hiệu
Đầu tiên, ký hiệu chỉ z là hàm theo 1 biến x, trong khi đó, biểu thức xác định của z là:
nên với ký hiệu này ta sẽ hiểu là z là hàm số hợp của 1 biến x thông qua biến trung gian y.
Còn ký hiệu, chỉ đạo hàm riêng của z theo biến x, điều này được hiểu là z là hàm hai theo 2 biến độc lập x, y.
Như vậy:
Còn:
Ví dụ 2: Tìm biết
Bạn có thể lập sơ đồ xích cho 3 biến r, s, t để xác định công thức tính đạo hàm như sau:
 Dựa vào sơ đồ trên, ta có:
Dựa vào sơ đồ trên, ta có:
,
Việc còn lại bạn làm tiếp tục nhé.
Ví dụ 3: Tìm
Ta đặt: thì f là hàm số hợp của 2 biến x, y thông qua 2 biến trung gian u, v.
Khi đó:
4. Đạo hàm cấp 2 của hàm số hợp 2 biến:
Giả sử z là hàm số hợp theo 2 biến x, y thông qua 2 biến trung gian u, v. Khi đó ta đã có công thức tính đạo hàm riêng cấp 1 của z đối với 2 biến x, y. Vấn đề đặt ra là: vậy nếu cần tính tiếp tục đạo hàm riêng cấp 2 của hàm số hợp thì ta phải làm thế nào?
Ta chú ý, trong công thức:
Các đại lượng lại là các biểu thức theo u, v nên nó lại là những hàm số hợp của hai biến x, y thông qua 2 biến trung gian u, v.
Do đó:
(*)
Mặt khác, áp dụng quy tắc tính đạo hàm hàm số hợp cho 2 hàm . Ta có:
,
(**)
Từ (*), (**) ta có:
Hoàn toàn tương tự, ta tìm được công thức xác định (bạn thử tìm xem nhé)
Ví dụ áp dụng: Tìm nếu
Đáp số:
Tình huống:
Cho y là hàm theo biến số x xác định từ phương trình:
.Bạn thử tìm đạo hàm:
.
Nếu giải tìm được y theo x thì bài toán quá dễ dàng. Còn nếu không giải tìm được hàm y theo biến x thì thế nào đây?
Đánh giá:
Chia sẻ:
- In
Thảo luận
27 bình luận về “Đạo hàm của hàm hợp”
Bình luận về bài viết này Hủy trả lời
Từ khóa » đạo Hàm Riêng Cấp 1 Bằng Quy Tắc Mắt Xích
-
GIẢI TÍCH B2 (Vi Tích Phân Của Hàm Số Nhiều Biến) JAMES ... - Issuu
-
Bài Tập đạo Hàm Riêng Cấp 1 Của Hàm Nhiều Biến Bằng Quy Tắc
-
GIẢI TÍCH B2 (Vi Tích Phân Của Hàm Số Nhiều Biến) JAMES ...
-
Bai Tap Co Loi Giai Dao Hamieng_va_vi_phan - SlideShare
-
[Giải Tích] Đạo Hàm Của Hàm Nhiều Biến Số - Hai's Blog
-
Bài Tập đạo Hàm Riêng Cấp 1 Của Hàm Nhiều Biến Bằng Quy Tắc
-
GIẢI TÍCH B2 Vi Tích Phân Của Hàm Số Nhiều Biến - Tài Liệu Text
-
Bài Giảng Giải Tích B2 - ĐH Khoa Học Tự Nhiên TP. HCM - TailieuXANH
-
Slide Giai Tich B2 - 2018 | PDF - Scribd
-
[PDF] Đạo Hàm, Tích Phân ứng Dụng được Gì? - Interactive Mathematics
-
Cách Làm Bài Tập đạo Hàm Riêng Cấp 1 Và Cấp 2 - Học 3 Giây
-
Đạo Hàm – Wikipedia Tiếng Việt
-
Tìm Hiểu Cách Tính đạo Hàm Của Hàm Hợp Cực Hay Và Cực Dễ
cho em hỏi bài này Z= f(e^xy- e^(-xy)) Tính ∂z/∂x=? ∂z/∂y=?
ThíchThích
Được đăng bởi Tình Thái | 17/12/2016, 21:52 Reply to this commentthầy giúp em giải bài này được k ạ, tính đạo hàm riêng của hàm f(x,y)=tg(x+y).e^(x/y)
ThíchThích
Được đăng bởi diepvien007 | 03/03/2013, 13:05 Reply to this commentem cảm hơn thầy nhiều ,khi đọc bài của thầy em đã phần nào hiểu ra rất nhiều
ThíchThích
Được đăng bởi Thanh Thủy | 22/11/2012, 17:40 Reply to this commentThầy có thể vừa giải vừa nêu cách làm cho dạg bài sau gjúp em với ! Y={x^2 . e^(-x^2) khi |x|1} e xjn cám ơn thầy !
ThíchThích
Được đăng bởi Kartos | 28/12/2011, 18:18 Reply to this commentThầy cho em hỏi : côg thức ngắn gọn và dễ hiểu nhất về đạo hàm hàm 2 biến số . (thầy cứ xem như là em chưa học về đh hàm đa biến ) Em xin cám ơn !
ThíchThích
Được đăng bởi Kartos | 28/12/2011, 12:13 Reply to this commentThay cho em hoi dao ham cua ham z= xy+x.f(y/x) tinh nhu the nao a. Cam on thay.
ThíchThích
Được đăng bởi Thu thao | 03/12/2011, 18:50 Reply to this commentcảm ơn thầy nhiều lắm. em đang cần tìm hiểu đạo hàm cấp cao của hàm số hợp. đọc xong giải tỏa được nhiều khúc mắc ^^. hay lắm ạ
ThíchThích
Được đăng bởi Huỳnh | 03/12/2011, 16:58 Reply to this commentchỉ lý thuyết suôn ai hiểu chết liền.
ThíchThích
Được đăng bởi lê lộc | 08/11/2011, 18:30 Reply to this commentCảm ơn bạn đã góp ý. Có thể đối với người này thì dễ hiểu, đối với người khác thì rất khó hiểu. Chính vì vậy, chúng ta mới cần trao đổi để nắm rõ vấn đề. Nếu bạn bình tâm đọc, suy ngẫm các hướng dẫn và xem lại các ví dụ, có thể bạn sẽ nắm được nội dung của vấn đề. Nếu chỗ nào chưa rõ, hoặc không hiểu, bạn cứ mạnh dạn trao đổi để mọi người có thể hướng dẫn cho bạn. Quan điểm của tôi là không làm thay các bạn, mà chỉ định hướng, hướng dẫn để các bạn tự tin vào bản thân mình và tự tìm được các kết quả. Hy vọng bạn sẽ tìm được 1 chút gì đó hữu ích từ trang web này.
ThíchThích
Được đăng bởi 2Bo02B | 08/11/2011, 19:25 Reply to this commentThầy cho em hỏi đạo hàm riêng của 1/căn bậc 2 (x^2 + y^2 + z^2) theo từng biến thì tính thế nào ạ em xin cảm ơn thầy
ThíchThích
Được đăng bởi Hà Nguyễn | 02/11/2011, 03:33 Reply to this commentĐạo hàm riêng theo biến nào thì các biến khác là hằng số. Ta có: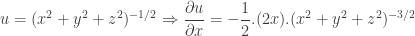 tương tự cho đạo hàm riêng theo biến y và z.
tương tự cho đạo hàm riêng theo biến y và z.
ThíchThích
Được đăng bởi 2Bo02B | 02/11/2011, 07:29 Reply to this comment