Đạo Hàm Riêng | Maths 4 Physics & More...
Có thể bạn quan tâm
I. Đạo hàm riêng cấp một:
Cho z = f(x,y) là hàm theo hai biến số độc lập x, y.
Bây giờ, ta cố định giá trị của biến số y (cho y là hằng số).
Như vậy, ta sẽ có hàm số theo 1 biến số x. Ta xem xét sự thay đổi của hàm số mới này theo biến số x.
Giả sử rằng hàm số z = f(x,y) (coi y là hằng số) có đạo hàm theo biến số x, thì giá trị đạo hàm này sẽ là:
Ta ký hiệu giới hạn trên là , trong đó biến x ở chỉ số dưới, ngầm chỉ rằng đạo hàm được lấy theo biến x khi cố định biến y. Và gọi là đạo hàm riêng của hàm f theo biến x.
Vậy: chúng ta định nghĩa đạo hàm riêng của hàm f(x, y) theo biến x tại điểm (x0, y0) như là đạo hàm thường của hàm f(x, y0) tại điểm x = x0
I.1 Định nghĩa:
Đạo hàm riêng theo biến x của hàm z = f(x, y) tại điểm (x0, y0) là giới hạn (nếu có)
và được ký hiệu là đọc là “del f del x” “del z del x”.
Rõ ràng ta có:
Tương tự, ta có đạo hàm riêng theo biến số y:
Nhận xét:
1. Để chỉ ký hiệu đạo hàm riêng, ta dùng ký hiệu thay cho ký hiệu
(vốn dùng để ký hiệu đạo hàm thường – đạo hàm của hàm 1 biến)
2 . Để tính đạo hàm riêng theo biến x, ta chỉ việc xem các biến còn lại là các hằng số và lấy đạo hàm như hàm số 1 biến số x.
3 . Các quy tắc lấy đạo hàm thường vẫn đúng trong trường hợp lấy đạo hàm riêng.
4. Trong thực hành, để tính , dựa vào định nghĩa, ta có hai cách:
- Cách 1: tìm
, suy ra
( trong trường hợp hàm số
xác định tại (x0, y0).
- Cách 2: Theo định nghĩa, Lập hàm
tìm
, suy ra giá trị
thì đây chính là giá trị
5. Khi hàm số z = f(x, y) có các đạo hàm riêng theo các biến, vecto có các thành phần lần lượt là các đạo hàm riêng theo các biến của hàm f được gọi là vecto gradient, ký hiệu
Ta còn dùng ký hiệu thay cho
. Ta sẽ đề cập chi tiết về grad f trong các phần sau.
II.2 Các ví dụ:
Ví dụ 1. Tính biết
Ta tính các đạo hàm riêng theo 2 cách:
Cách 1:
Suy ra:
Do đó:
Cách 2: Tính :
Thay giá trị y = 1, ta nhận được: là hàm theo một biến (biến x). Lúc này:
tương tự: là hàm theo một biến y và
Cả hai cách trên ta có cùng 1 kết quả. Bấy giờ, ta suy ra:
Tuy nhiên, để tìm thì rõ ràng cách 1 là tổng quát hơn, còn cách 2 chỉ có thể tìm được giá trị của đạo hàm tại 1 điểm cụ thể.
Ví dụ 2: Cho hàm
Tìm
Với hàm số f(x,y) này, ta không thể tìm hàm đạo hàm riêng , rồi suy ra giá trị đạo hàm riêng tại (0,0), vì hai hàm
chỉ xác định với mọi (x,y) khác (0, 0).
Do đó, ta phải dùng định nghĩa để tính giá trị . Ta có:
Tương tự, ta cũng nhận được
Nhận xét:
1. Trong trường hợp này, ta có thể sử dụng cách 2 để tìm .
2. Ta đã biết: đối với hàm số 1 biến, nếu hàm số có đạo hàm tại x0 thì sẽ liên tục tại điểm đó. Tuy nhiên, Theo lý thuyết về giới hạn hàm số hai biến, ta đã biết hàm số trên không liên tục tại điểm (0, 0) mặc dù hàm số trên có 2 đạo hàm riêng tại (0,0). Vì vậy, việc tồn tại đạo hàm riêng chưa đảm bảo sự liên tục của hàm số.
Đánh giá:
Chia sẻ:
- In
Trang: 1 2
Thảo luận
50 bình luận về “Đạo hàm riêng”
Bình luận về bài viết này Hủy trả lời
Từ khóa » đạo Hàm Riêng Cấp 1 Arctan X/y
-
Tìm Đạo Hàm - D/dx Arctan(x/y) - Mathway
-
Bài Tập đạo Hàm Riêng, đạo Hàm Theo Hướng Có đáp án - 123doc
-
Bài 1 Tính Các đạo Hàm Riêng Cấp 1
-
[PDF] BÀI GIẢNG TOÁN CAO CẤP A1
-
đạo Hàm Riêng Arctan Y/x | Lịchcắttó
-
[PDF] BÀI TẬP HỌC PHẦN TOÁN CAO CẤP - FITA-VNUA
-
[PDF] Bài Giảng Toán Cao Cấp PGS.TS Lê An
-
01 GT2 Dao Ham Rieng By DAT NGUYEN - Issuu
-
P2: Các Công Thức Tính đạo Hàm Cần Nhớ (4) - YouTube
-
[TOÁN CAO CẤP - CHUYÊN ĐỀ 12] BÀI 12.1 - ĐẠO HÀM RIÊNG ...
-
Bai Tap Co Loi Giai Dao Hamieng_va_vi_phan - SlideShare
Dạ, Em chào Thầy. ở ví dụ 2: Thầy nói đạo hàm theo biến x và đạo hàm theo biến y của hàm f không xác định tại điểm (0,0). Không biết Thầy có đánh máy nhầm không. Hàm f không khả vi, nhưng đạo hàm riêng luôn tồn tại tại mọi điểm xác định.
ThíchThích
Được đăng bởi hoanen | 16/01/2011, 21:55 Reply to this commenttheo mình không nhầm đâu bạn nếu bạn cứ máy móc sử dụng công thức tính đạo hàm riêng thì sẽ đưa bạn đến dạng vô định của đạo hàm riêng tại điểm (0,0) , ý của bài toán là muốn bạn phải sử dụng định nghĩa để tính đạo hàm riêng thôi mà
ThíchThích
Được đăng bởi hoivudai | 15/02/2011, 23:17 Reply to this commentThầy giúp em giải câu này ạ: z=(x-2y).cos(x-2y)+arctg(x+2y) tinh Z”xx ;Z”yy
ThíchThích
Được đăng bởi xuan tien | 04/01/2011, 06:56 Reply to this commentBài này là dạng đạo hàm riêng theo biến x của hàm 2 biến, nên bạn cứ lấy đạo hàm bình thường thôi mà. Ta có: Z”xx =(z’x)’x nên trước tiên bạn tìm z’x. Sau đó, lấy đạo hàm của z’x theo biến x lần nữa thì bạn sẽ có kết quả. Ví dụ: z’x = 1.cos(x-2y) + (x-2y).1.(-sin(x-2y)) + 1/(1+(x+2y)^2) Bạn làm tiếp nhé.
ThíchThích
Được đăng bởi Vũ Hoàng | 04/01/2011, 17:06 Reply to this commente cám ơn thầy nhiều. thầy giảng dễ hiểu quá.
ThíchThích
Được đăng bởi thanh tâm | 03/01/2011, 09:00 Reply to this commentthầy ơi giải giúp e. giải pt x.z’(x)+y.z’(y)=0. bằng cách đặt x= rcosφ, y= rsinφ. đây là pt của hàm 2 biến với z’(x) la đạo hàm của z’ theo biến x, còn z’(y) là đạo hàm của z’ theo biến y.
ThíchThích
Được đăng bởi thanh tâm | 02/01/2011, 08:00 Reply to this commentTa có: z là hàm theo 2 biến (x;y), còn (x;y) lại là hàm theo hai biến (r, φ) nên z là hàm số hợp của 2 biến (r, φ) thông qua 2 biến trung gian (x,y). Khi đó: sử dụng công thức đạo hàm hàm hợp, em có: Từ đó, em tìm được z'(x), z'(y) theo z'(r) và z'(φ) và thế vào pt, em sẽ có pt là:
Từ đó, em tìm được z'(x), z'(y) theo z'(r) và z'(φ) và thế vào pt, em sẽ có pt là: 
ThíchThích
Được đăng bởi 2Bo02B | 02/01/2011, 22:27 Reply to this commentthầy ơi giúp em bài này với ạ: 1. Tính biểu thức
Tính biểu thức 
ThíchThích
Được đăng bởi ngaymai | 30/11/2010, 19:28 Reply to this commentEm chú ý: g(v) là một hàm tổng quát chưa biết, ta chỉ biết nó phụ thuộc vào v = y – x. Như vậy, g là hàm theo 2 biến x, y được định nghĩa thông qua biến trung gian v. Vậy g là hàm hợp. Vậy, em lấy đạo hàm của g theo biến y bằng quy tắc đạo hàm hàm hợp. Cụ thể: Suy ra:
Suy ra:  Hay:
Hay:  Tức là:
Tức là:  vậy:
vậy: 
ThíchThích
Được đăng bởi 2Bo02B | 30/11/2010, 22:29 Reply to this commentThầy giúp em bài này với ạ, em sắp thi cuối kì rồi mà em vẫn chưa nắm được phần đạo hàm 1. Tìm u’x nếu có 2 phương trình: Ở đó y = y(x); u = u(x)
Ở đó y = y(x); u = u(x)
ThíchThích
Được đăng bởi ngaymai | 28/11/2010, 20:04 Reply to this commentĐề bài cho y = y(x); u = u(x), xác định bởi hệ pt. Nghĩa là: y và u là 2 hàm ẩn theo biến số x. Em xem phần đạo hàm của hàm số ẩn nhé. Đây là trường hợp hệ hàm ẩn. Pp chung là em lấy đạo hàm hệ pt theo biến số x. Em sẽ có hpt mới với 2 ẩn là u’x và y’x. Giải hpt mới này, em sẽ tìm được u’x theo u, x, y. Cụ thể:

ThíchThích
Được đăng bởi 2Bo02B | 28/11/2010, 21:31 Reply to this commentthầy ơi em hỏi chút sao khi tính Y’x lại còn cả Y thế tính Y’x thì làm thế nào ak.
ThíchThích
Được đăng bởi giag | 03/12/2010, 16:37 Reply to this commentEm xem bài đạo hàm hàm ẩn nhé. Vì là hàm ẩn nên có nhiều bài không thể tìm được cụ thể dạng tường minh của hàm số y theo biến số x. Nên kết quả y’ (tốc độ thay đổi giá trị của hàm số) sẽ phụ thuộc vào hàm số y. Trong thực tế, vẫn có những hàm có đạo hàm y’ phụ thuộc y. Ví dụ: . Tuy nhiên, trong trường hợp này, do ta tìm được hàm y nên kq khi thế
. Tuy nhiên, trong trường hợp này, do ta tìm được hàm y nên kq khi thế  vào thì y’ không còn phụ thuộc y.
vào thì y’ không còn phụ thuộc y.
ThíchThích
Được đăng bởi 2Bo02B | 04/12/2010, 21:33Thầy Thụ Nhân kính mến!
Em thấy các tài liệu hiện hành không thống nhất trong việc kí hiệu đạo hàm riêng cấp cao. Theo cách của thầy (và một số giáo trình khác, ví dụ [b]Giải Tích, tập 1, Nguyễn Xuân Liêm, NXB GD 1997[/b]) thì
Tuy nhiên, trong một số tài liệu (điển hình là cuốn [b]Toán cao cấp, tập II(A2), Nguyễn Văn Khuê (cb), Phạm Ngọc Thao, Lê Mậu Hải, Nguyễn Đình Sang; NXB GD 1997[/b] – giáo trình chính thức của ĐHSPHN), thì
Rõ ràng không phải lúc nào hai cách viết này cũng cho cùng một kết quả. Vậy thì phải có một cách viết sai? Hay đang có một sự không thống nhất trong cách viết ở đây? Em thật sự thấy bối rối. Rất mong lời giải đáp của thầy.
Em cảm ơn thầy.
ThíchThích
Được đăng bởi Duc Lam | 29/05/2010, 13:50 Reply to this commentThầy hướng dẫn dùm em bài này :cho z=e^(xy) trong đó y=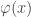 . Biết
. Biết 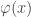 khả vi. Em ko biết cách tính đạo hàm y theo x.
khả vi. Em ko biết cách tính đạo hàm y theo x.
ThíchThích
Được đăng bởi histrix | 16/03/2010, 15:52 Reply to this commentThưa thầy, em muốn hỏi cách tính đạo hàm riêng bậc 2 của hàm nhiều biến (kiểu hàm hợp và hàm ẩn). Trong sách có ghi công thức này nhưng em ko hiểu, nhờ thầy chỉ dạy: Giả sử cho hàm ẩn: z^2(z+3x)+3y, CMR: (d2z/dx2)+(d2z/dy2)=(2xz-2z)/(z^2+x)^3. Trong sách em có ghi công thức như sau: d2z/dx2=d/dx(dz/dx). Em ko hiểu chỗ này! Mong thầy sớm hồi âm. Em xin cảm ơn!
ThíchThích
Được đăng bởi histrix | 15/03/2010, 08:47 Reply to this commentTheo lý thuyết, ký hiệu có nghĩa là đạo hàm riêng theo biến x của hàm đạo hàm riêng cấp 1:
có nghĩa là đạo hàm riêng theo biến x của hàm đạo hàm riêng cấp 1: 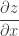 Khi đó: nếu em đặt
Khi đó: nếu em đặt  thì
thì  chính là đạo hàm riêng theo biến x của hàm g(x,y) nên ký hiệu:
chính là đạo hàm riêng theo biến x của hàm g(x,y) nên ký hiệu:  Hay:
Hay:  . Khi đó, ta có thể ký hiệu thành
. Khi đó, ta có thể ký hiệu thành 
ThíchThích
Được đăng bởi 2Bo02B | 15/03/2010, 14:18 Reply to this commentem cảm ơn thầy. H em hiểu rồi, vì trong sách có bài ví dụ, nhưng là của hàm e^x, hoặc ra kết quả lun. Thầy giảng dễ hiểu lắm ạ! 🙂
ThíchThích
Được đăng bởi histrix | 15/03/2010, 22:39 Reply to this commente chào Thầy!Thầy giúp dùm e bài này nha Thầy.e ko biết chèn công thức vô nên Thầy thông cảm.Biết z(z^2 + 3x) + 3y =0. CMR : đạo hàm z 2 lần theo x + đạo hàm z 2 lần theo y =2z(x-1)/(z^2 + x)^3. Thầy giúp dùm e nha!!e cám ơn thầy nhiều!!
ThíchThích
Được đăng bởi Thanh Tuyền | 14/03/2010, 21:58 Reply to this commentDựa vào yêu cầu của bài toán Ta có: z là hàm ẩn theo 2 biến x, y được xác định bởi pt: Do đó, sử dụng công thức đạo hàm hàm ẩn, em tìm được
Do đó, sử dụng công thức đạo hàm hàm ẩn, em tìm được  Từ đó, em tìm được
Từ đó, em tìm được  (em lưu ý ở đây khi lấy đạo hàm thì z là hàm theo biến x nhé). Nghĩa là:
(em lưu ý ở đây khi lấy đạo hàm thì z là hàm theo biến x nhé). Nghĩa là:  Em làm tương tự với
Em làm tương tự với  Ráp vào em sẽ có điều cần chứng minh. Em có thể tham khảo thêm phần đạo hàm hàm số ẩn để hiểu rõ hơn nhé.
Ráp vào em sẽ có điều cần chứng minh. Em có thể tham khảo thêm phần đạo hàm hàm số ẩn để hiểu rõ hơn nhé.
ThíchThích
Được đăng bởi 2Bo02B | 15/03/2010, 14:16 Reply to this commentthầy ơi cho em hỏi để nhận biết hai đạo hàm đối nhau x,y trong giai toán đạo hàm thi ta căn cứ và dựa vào dấu hiệu nhận biết nào thưa thầy. Em cảm ơn thầy nhiều!
ThíchThích
Được đăng bởi Đinh luyện | 04/03/2010, 14:46 Reply to this commentNếu trong hàm z= f(x,y), x, y có vai trò như nhau thì sau khi em tính , em chỉ cần thế x bằng y và y bằng x (đổi vai trò của x, y) thì em sẽ được
, em chỉ cần thế x bằng y và y bằng x (đổi vai trò của x, y) thì em sẽ được  . Cái này là hệ quả được suy ra từ định nghĩa của đạo hàm riêng.
. Cái này là hệ quả được suy ra từ định nghĩa của đạo hàm riêng.
ThíchThích
Được đăng bởi 2Bo02B | 04/03/2010, 20:42 Reply to this commentThưa Thầy, em muốn biết bản chất F”xy thì tính đạo hàm của hàm số theo x trước rồi mới tính theo y hay là ngược lại vậy ạ. Tại vì có nhiều tài liệu viết khác nhau quá nên em ko biết làm sao, với lại vì tính đối xứng của đạo hàm riêng cấp 2 mà người ta để nhầm lẫn ko biết tính đạo hàm theo biến nào trước, mong thầy trả lời giúp em sớm nhất trong 1 ngày được không ạ, em đang rất cần, em cảm ơn thầy nhiều lắm ạ !!!
ThíchThích
Được đăng bởi Nguyen Tien Anh | 17/12/2009, 19:19 Reply to this commentĐúng như em nói, hiện có 2 trường phái về ký hiệu F”xy. Một trường phái là ký hiệu (theo thứ tự từ trái sang phải), một trường phái ký hiệu
(theo thứ tự từ trái sang phải), một trường phái ký hiệu  (theo thứ tự từ phải sang trái). Do đó, khi đọc giáo trình, trước tiên, em nên coi phần định nghĩa đạo hàm cấp hai của hàm nhiều biến, để biết cách mà người viết ký hiệu. Tuy vậy, đối với những hàm số liên tục, có đạo hàm riêng liên tục thì việc lấy đạo hàm không phụ thuộc thứ tự lấy, nên lấy cách nào cũng không sao.
(theo thứ tự từ phải sang trái). Do đó, khi đọc giáo trình, trước tiên, em nên coi phần định nghĩa đạo hàm cấp hai của hàm nhiều biến, để biết cách mà người viết ký hiệu. Tuy vậy, đối với những hàm số liên tục, có đạo hàm riêng liên tục thì việc lấy đạo hàm không phụ thuộc thứ tự lấy, nên lấy cách nào cũng không sao.
ThíchThích
Được đăng bởi 2Bo02B | 17/12/2009, 21:34 Reply to this comment