Đáp án đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GDĐT Đà Nẵng (2018 ...

Mục lục nội dung Đáp án đề thi tuyển sinh lớp 10 môn ToánSở GDĐT Đà Nẵng (2018-2019)

Đáp án đề thi tuyển sinh lớp 10 môn Toán

Sở GDĐT Đà Nẵng (2018-2019)

Bài 1. (1,5 điểm)

a, Trục căn thức ở mẫu của biểu thức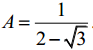 

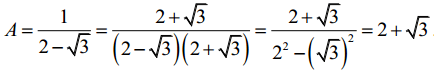
b, Cho a ≥ 0, a ≠ 4. Chứng minh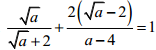 

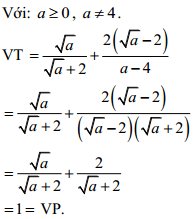
Vậy đẳng thức đã được chứng minh

Bài 2. ( 2,0 điểm)

a, Giải hệ phương trình

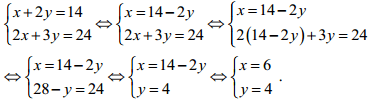
Vậy nghiệm của hệ phương trình là (x; y) = (6;4)  

b) Giải phương trình

Điều kiện: x ≠ 1.

 

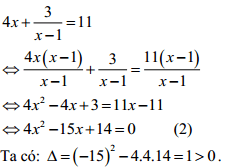
Vậy phương trình (2) có 2 nghiệm phân biệt là: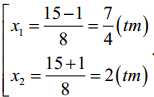 

Vậy phương trình đã cho có tập nghiệm là: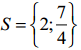

Bài 3. (1,5 điểm)

+) Vẽ đồ thị hàm số

x	-4	-2	0	2	4
y	-8	-2	0	-2	-8

Khi đó đồ  thị hàm số  có hình dạng là 1 Parabol và đi qua các điểm (-4; -8);  (-2; -2); (0;0); (2; -2); (4; -8) .

+) Vẽ đô thị hàm sô: y = x - 4.

x	0	4
y	-4	0

Khi đó đồ thị hàm số y = x - 4 là một đường thẳng và đi qua các điểm (0; -4) ; (4; 0) .

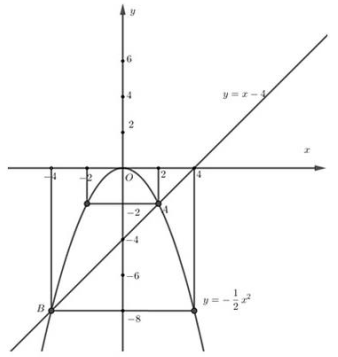
+) Phương trình hoành độ giao điểm của hàm số  và y = x - 4 là:

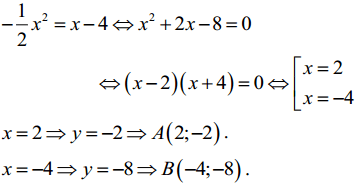
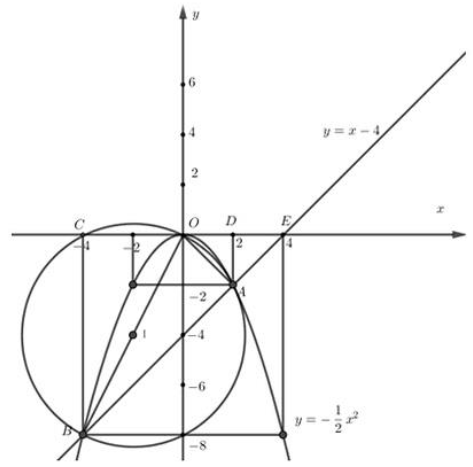
Xét tam giác OAE ta có: OD = DE = OE = 2 cm; AD = 2 cm nên tam giác OAE vuông tại A.

Khi đó ta có : OA ⊥ AB nên tam giác OAB vuông tại A.

Ta có tâm đường tròn ngoại tiếp tam giác OAB là trung điểm của cạnh huyền OB và bán kính của đường tròn 

Ta có: Áp dụng định lí Pitago trong tam giác vuông OBC có:

OB2 = OC2 + BC2 = 42 + 82 = 80

Vậy bán kính đường tròn ngoại tiếp tam giác OAB là 

Bài 4. (1,0 điểm)

Phưong trình có hai nghiệm phân biệt x1, x2 ⇔ ∆' > 0.

⇔ (m-1)2 -4m + 11 > 0

⇔m2 - 2m +1 - 4m +11 > 0

⇔m2 - 6m + 12 > 0

⇔m2 - 6m + 9 + 3 > 0

⇔ (m - 3) + 3 > 0.

Vì (m -3)2 ≥ 0 m ⇒ (m -3)2 + 3 > 0 m ⇒ ∆’> 0 m .

Hay phương trình đã cho luôn có hai nghiệm phân biệt x1, x2 với mọi m .

Áp dụng hệ thức Vi - ét ta có: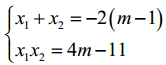 

Vì x1, x2 là nghiệm của phưong trình x2 + 2(m -1)x + 4m -11 = 0 nên ta có:

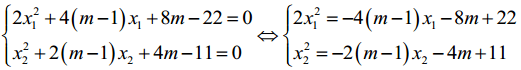
2(x1 -1)2 + (6 – x2 ) (x1x2 + 11) = 72

⇔ -4 (m - 1) x1 - 8m + 22 - 4x1 + 6x1x2 - x1(-2 (m - 1) x2 - 4m + 11) - 11x2 = 4

⇔ 4mx1 + 4x1 - 8m + 22 – 4x1 + 6x1x2 + 2 (m - 1) x1x2 + 4mx1 -11x1 -11x2 = 4

⇔(2m + 4) x1x2 - 11( x1 + x2) = 8m - 18

⇔(2m + 4)( 4m - 11) + 22 (m - 1) = 8m - 18

⇔ 8m2 - 22m + 16m - 44 + 22m - 22 = 8m - 18

⇔ 8m2 + 8m - 48 = 0

⇔m2 + m - 6 = 0

⇔m2 - 2m + 3m - 6 = 0

⇔m (m - 2) + 3 (m - 2) = 0

⇔ (m + 3)( m - 2) = 0

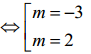
Vậy m = -3 hoặc m = 2 thỏa mãn yêu cầu bài toán.

Bài 5.(1,0 điểm)

Gọi độ dài một cạnh góc vuông lớn hơn của tam giác vuông là x (cm), (7 < x < 17) .

Khi đó độ dài cạnh góc vuông còn lại của tam giác vuông đó là : x - 7 (cm). Áp dụng định lí Pi - ta - go cho tam giác vuông này ta có phương trình :

x2 +(x - 7 )2 =172

⇔ 2x2 - 14x + 49 = 289

⇔ 2x2 -14x - 240 = 0

⇔ 2 (x -15)( x + 8) = 0

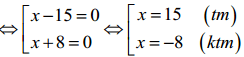
⇒ độ dài cạnh còn lại của tam giác vuông là: 15 – 7=8 cm

Vậy diện tích của tam giác vuông đó là :

Bài 6.( 3,0 điểm)

 

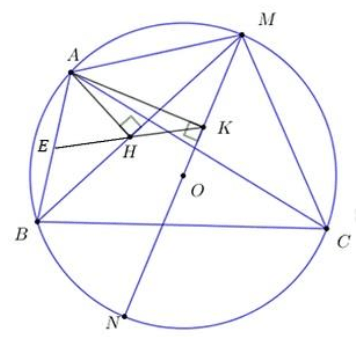
a, Bốn điểm A, H, K, M cùng nằm trên một đường tròn.

Xét tứ giác AHKM ta có: ∠AHM = ∠AKM = 90° (gt).

Mà hai góc này là góc kề cạnh HK và cùng nhìn đoạn AM .

⇒AHKM là tứ giác nội tiếp (dấu hiệu nhận biết).

Hay bốn điểm A, H, K, M cùng nằm trên một đường tròn ( đpcm ) .

b, AH.AK = HBMK.

Ta có:

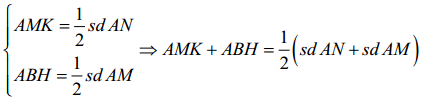
Mà sdAN + sdAM = sdMAN = 180°=> ∠AMK + ∠ABH = 90°.

Mà ∠ABH + ∠BAH = 90° (tam giác ABH vuông tại H).

⇒ ∠AMK = ∠BAH .

Xét tam giác AMK và tam giác BAH có:

∠AKM = ∠BHA = 90°

∠AMK = ∠BAH (cmt)

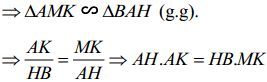
c) Khi điểm M di động trên cung nhỏ AC thì đường thẳng HK luôn qua một điểm cố định. Kéo dài HK cắt AB tại

Ta có ∠MAK = ∠MHK (hai góc nội tiếp cùng chắn cung MK ).

Lại có ∠MHK = ∠EHB ( đối đỉnh)

=> ∠MAK = ∠EHB

Do   => ∠MAK = ∠ABH = ∠EBH

=> ∠EHB = ∠EBH     => ∆EHB cân tại E.

=> EH = EB (1).

Ta có ∠EBH + ∠EAH = 90° (Tam giác ABH vuông tại H).

∠EHB + ∠EHA = ∠AHB = 90°

=> ∠EAH = ∠EHA => ∆EAH cân tại E

=> EA = EH (2).

Từ (1) và (2) => EA = EB =>E là trung điểm của AB . Do A, B cố định => E cố định.

Vậy khi M di chuyển trên cung nhỏ AC thì HK luôn đi qua trung điểm của AB (đpcm) .