Đề Cương ôn Tập Học Kì 1 Môn Toán Lớp 11
Có thể bạn quan tâm
-
-

-
Mầm non
-
Lớp 1
-
Lớp 2
-
Lớp 3
-
Lớp 4
-
Lớp 5
-
Lớp 6
-
Lớp 7
-
Lớp 8
-
Lớp 9
-
Lớp 10
-
Lớp 11
-
Lớp 12
-
Thi vào lớp 6
-
Thi vào lớp 10
-
Thi Tốt Nghiệp THPT
-
Đánh Giá Năng Lực
-
Khóa Học Trực Tuyến
-
Hỏi bài
-
Trắc nghiệm Online
-
Tiếng Anh
-
Thư viện Học liệu
-
Bài tập Cuối tuần
-
Bài tập Hàng ngày
-
Thư viện Đề thi
-
Giáo án - Bài giảng
-
Tất cả danh mục
-
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp
-
- Hôm nay +3
- Ngày 2 +3
- Ngày 3 +3
- Ngày 4 +3
- Ngày 5 +3
- Ngày 6 +3
- Ngày 7 +5
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo xf xxxf xxxf xxyx xyxxyxyxyxyxf xxx fxxx fxxxxxooxxoxxxxxxxx x x xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxx
xf xxxf xxxf xxyx xyxxyxyxyxyxf xxx fxxx fxxxxxooxxoxxxxxxxx x x xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxx  xxxxxxxxxxxxxx xxxxxxxxxxxx-+=xxxx--=xx xx xxxx xx xxxxxxxxxxxx xxxxxxxxxx xxxxxxxxxxx xxxxxxxxx
xxxxxxxxxxxxxx xxxxxxxxxxxx-+=xxxx--=xx xx xxxx xx xxxxxxxxxxxx xxxxxxxxxx xxxxxxxxxxx xxxxxxxxx  0 xyxy xx
0 xyxy xx Nội dung ôn thi học kì I môn Toán lớp 11
Đề cương ôn tập học kì 1 môn Toán lớp 11 vừa được VnDoc.com sưu tập và xin gửi tới bạn đọc để bạn đọc cùng tham khảo và có thêm tài liệu ôn tập. Đề cương gồm có 9 trang gồm kiến thức các phần Đại số và Hình học trong toán 11 học kì 1, phía cuối là một số đề thi tham khảo. Mời bạn đọc cùng tham khảo chi tiết bài viết dưới đây nhé.
ĐỀ CƯƠNG ÔN TẬP TOÁN 11HỌC KÌ 1 – CHUẨN VÀ NÂNG CAO
I. HÀM SỐ LƯỢNG GIÁC – PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Tìm tập xác định của mỗi hàm số sau đây:
a.
Điều kiện xác định:
Vậy tập xác định của hàm số là:
b.
Điều kiện xác định của hàm số:
Vậy tập xác định của hàm số là:
c.
Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số là:
d.
Điều kiện xác định của hàm số:
Vậy tập xác định của hàm số là:
2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a.
Ta có:
Giá trị lớn nhất của hàm số là:
Giá trị nhỏ nhất của hàm số là:
b.
Ta có:
Giá trị lớn nhất của hàm số là:
Giá trị nhỏ nhất của hàm số là:
c.
Tương tự câu trên ta dễ dàng chỉ ra
Giá trị lớn nhất của hàm số là:
Giá trị nhỏ nhất của hàm số là:
d.
Ta có:
Giá trị lớn nhất của hàm số là:
Giá trị nhỏ nhất của hàm số là:
f.
Ta có:
Giá trị lớn nhất của hàm số là:
Giá trị nhỏ nhất của hàm số là:
1.3. Giải phương trình lượng giác cơ bản:
Hướng dẫn giải
a.
Vậy phương trình có nghiệm hoặc
b.
Vậy phương trình có nghiệm hoặc
c.
Điều kiện:
Phương trình tương đương:
Vậy phương trình có nghiệm
d.
Vậy phương trình có nghiệm
Các câu còn lại học sinh tự giải
1.4. Giải các phương trình lượng giác sau đây:
Hướng dẫn giải
a.
b.
Vậy phương trình có nghiệm:
1.5. Tìm các nghiệm của phương trình sau trong khoảng đã cho:
a/ 2sin2x + 1 = 0 với 0 < x < π
b/ cot(x - 5) = √3 với -π < x < π
Hướng dẫn giải
a.
Do phương trình có nghiệm nằm trong khoảng nên ta xét các trường hợp như sau:
Với ta có:
Với
Vậy trên khoảng phương trình có nghiệm
1. 6. Giải các phương trình sau:
1. 7. Giải phương trình:
1. 8. Giải phương trình:
![]()
1. 9. Giải phương trình:
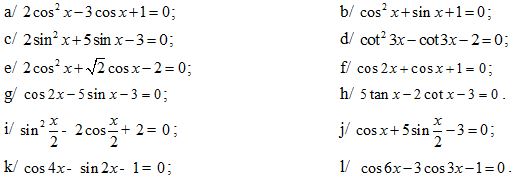
1. 10. Giải các phương trình:
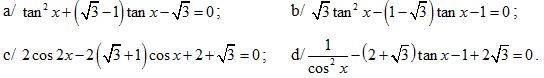
1. 11. Giải phương trình:

1. 12. Giải phương trình:

1. 13. Giải phương trình:
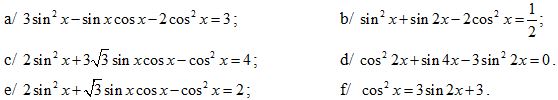
II. TỔ HỢP – XÁC SUẤT
2. 1. Có bao nhiêu số tự nhiên có hai chữ số mà hai chữ số của nó đều chẵn?
2. 2. Từ các chữ số 0, 1, 2, 3, 4, 5, 6, có thể tạo nên bao nhiêu số tự nhiên có hai chữ số khác nhau?
2. 3. Từ các chữ số 2, 3, 4, 6, 7 có thể lập được bao nhiêu số tự nhiên bé hơn 100?
2. 4. Cho tập hợp X = {0, 1, 2, 3, 4, 5, 6, 7, 8}. Từ các phần tử của tập X có thể lập bao nhiêu số tự nhiên trong các trường hợp sau:
a/ Số đó có 4 chữ số khác nhau từng đôi một.
b/ Số đó là số chẵn và có 4 chữ số khác nhau từng đôi một.
2. 5. Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau và chia hết cho 5?
2. 6. Có tối đa bao nhiêu số máy điện thoại có 7 chữ số bắt đầu bằng số 8 sao cho:
a/ Các chữ số đôi một khác nhau.
b/ Các chữ số tùy ý.
2. 7. a/ Có bao nhiêu cách chọn 3 người từ 10 người để thực hiện cùng một công việc?
b/ Có bao nhiêu cách chọn 3 người từ 10 người để thực hiện ba công việc khác nhau?
2. 8. Trong một cuộc thi có 16 đội tham dự, giả sử rằng không có hai đội nào cùng điểm.
a/ Nếu kết quả cuộc thi là chọn ra ba đội có điểm cao nhất thì có bao nhiêu cách chọn?
b/ Nếu kết quả cuộc thi là chọn ra các giải nhất, nhì, ba thì có bao nhiêu sự lựa chọn?
2. 9. Từ các chữ số 2, 3, 4, 5, 6, 7, 8 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau và lớn hơn 8600?
2. 10. Cho 10 điểm nằm trên một đường tròn.
a/ Có bao nhiêu đoạn thẳng mà hai đầu là hai trong số 10 điểm đã cho?
b/ Có bao nhiêu vectơ khác ![]() có gốc và ngọn trùng với hai trong số 10 điểm đã cho?
có gốc và ngọn trùng với hai trong số 10 điểm đã cho?
c/ Có bao nhiêu tam giác mà các đỉnh là ba trong số 10 điểm đã cho?
V. Quan hệ song song trong không gian
Bài 1. Cho hình chóp S.ABCD. Điểm M và N lần lượt thuộc các cạnh BC và SD.
a. Tìm I = BN (SAC).
b. Tìm J= MN (SAC).
c. Chứng minh I, J, C thẳng hàng
d. Xác định thiết diện của hình chóp với (BCN)
Bài 2. Cho tứ diện ABCD. Gọi E và F lần kượt là trung điểm của AD và CD và G trên đoạn AB sao cho GA= 2GB.
a. Tìm M = GE (BCD),
b. Tìm H = BC (EFG). Suy ra thiết diện của (EFG) với tứ diện ABCD. Thiết diện là hình gì?
c. Tìm (DGH) (ABC).
Bài 3. Cho hình chóp SABCD. Gọi O = ACBD. Một mặt phẳng (α) cắt SA, SB, SC, SD tại A’, B’, C’, D’. Giả sử AB
C’D = E, A’B’
C’D’ = E’.
a. Chứng minh: S, E, E’ thẳng hàng
b. Chứng minh A’C’, B’D’, SO đông quy.
Bài 4. Cho hình chóp SA BCD có đáy ABCD là hình bình hành.
a. Tìm (SAC) (SBD); (SAB)
(SCD), (SBC)
(SAD).
b. Một mặt phẳng qua CD, cắt SA và SB tại E và F. Tứ giác CDEF là hình gì? Chứng tỏ giao điểm của DE và CF luôn luôn ở trên 1 đường thẳng cố đinh.
c. Gọi M, N là trung điểm SD và BC. K là điểm trên đoạn SA sao cho KS = 2KA. Hãy tìm thiết diện của hình chop SABCD về(MNK)
Bài 5. Cho 2 hình bình hành ABCD và ABEF không đồng phẳng.
a. Gọi O và O’ là tâm của ABCD và ABEF. Chứng minh OO’//(ADF) và (BCE)
b. Gọi M, N là trọng tâm của ABD và
ABE. Chứng minh MN // (CEF)
Bài 6. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC, CD.
a. Chứng minh rằng MN // (ABD)
b. Gọi G và G’ lần lượt là trọng tâm ABC và
ACD. Chứng minh rằng GG’ // (BCD)
Bài 7. Cho hình chóp S.ABCD, đáy là hình thang ABCD với AB // CD và AB = 2CD
a. Tìm (SAD) (SCD).
b. M là trung điểm SA, tìm (MBC) (SAD) và (SCD)
c. Một mặt phẳng di động qua AB, cắt SC và SD tại H và K. Tứ giác ABHK là hình gì?
d. Chứng minh giao điểm của BK và AH luôn nằm trên 1 đường thẳng cố định.
Bài 8. Cho hình chóp SABCD. Gọi M, N, P lần lượt là trung điểm của SA, SD, BD
a. Chứng minh AD //(MNP)
b. NP // (SBC)
c. Tìm thiết diện của (MNP) với hình chóp. Thiết diện là hình gì?
Bài 9. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi M, N lần lượt là trung điểm của SA và SC.
a. Xác định thiết diện của hình chóp khi cắt bởi các mặt phẳng lần lượt qua M, N và song song với mặt phẳng (SBD).
b. Gọi I và J lần lượt là giao điểm của AC với hai mặt phẳng nói trên. Chứng minh .
Mời các bạn tải file đầy đủ về tham khảo.
Trên đây VnDoc.com vừa giới thiệu tới bạn đọc Đề cương ôn tập học kì 1 môn Toán lớp 11, chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Bài viết tổng hợp lại toàn bộ nội dung lý thuyết và các bài tập kèm theo trong học kì 1.... Mong rằng qua đây bạn đọc có thêm thật nhiều tài liệu và tổng hợp được kiến thức môn Toán để ôn tập tốt hơn nhé. Để giúp bạn đọc có thêm nhiều tài liệu học tập hơn nữa, VnDoc.com mời bạn đọc cùng tham khảo thêm một số tài liệu học tập các môn được chúng tôi biên soạn và tổng hợp tại các mục sau Ngữ văn 11, Tiếng Anh 11, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11...
- Đề cương ôn tập học kì 1 môn Vật lý lớp 11
- Đề cương ôn tập học kì 1 môn Ngữ văn lớp 11
- 20 bộ đề thi học kì 1 môn Toán lớp 11
- 20 bộ đề thi học kì 1 môn Toán lớp 1
Đề cương ôn tập học kì 1 môn Toán lớp 11
243,1 KB-
Tải file định dạng .DOC
54,5 KB
- Chia sẻ bởi:
 Kim Ngưu
Kim Ngưu

Có thể bạn quan tâm
Xác thực tài khoản!Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhấtTham khảo thêm
-
Đề thi học kì 1 môn Toán lớp 11 trường THPT Lê Hồng Phong, Đăk Lăk năm học 2015 - 2016
-
Cách tính góc giữa đường cao và mặt bên
-
Bộ 50+ bài tập trắc nghiệm Đường thẳng vuông góc với mặt phẳng (Có đáp án)
-
Cách chứng minh hai mặt phẳng vuông góc
-
Xác định thiết diện của hình chóp và lăng trụ khi cắt bởi mặt phẳng
-
Lý thuyết và bài tập Toán 11: Giới hạn của hàm số
-
Bộ 50+ bài tập Trắc nghiệm Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
-
Đề thi học kì 1 môn Toán lớp 11 trường THPT Trần Quang Khải, Hà Nội năm học 2015 - 2016
-
Đề kiểm tra học kì 1 môn Toán lớp 11 năm học 2014 - 2015 trường THPT Châu Thành 1, Đồng Tháp
-
Xác định góc giữa cạnh bên và mặt phẳng đáy
-
 Lớp 11
Lớp 11 -
 Đề thi học kì 1 lớp 11
Đề thi học kì 1 lớp 11 -
 Toán 11
Toán 11
Toán 11
-
Xác định thiết diện của hình chóp và lăng trụ khi cắt bởi mặt phẳng
-
Lý thuyết và bài tập Toán 11: Giới hạn của hàm số
-
Bộ 50+ bài tập Trắc nghiệm Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
-
Cách chứng minh hai mặt phẳng vuông góc
-
Bộ 50+ bài tập trắc nghiệm Đường thẳng vuông góc với mặt phẳng (Có đáp án)
-
Xác định góc giữa cạnh bên và mặt phẳng đáy

Gợi ý cho bạn
-
Trọng tâm của tứ diện là gì?
-
Bài tập tiếng Anh lớp 10 Unit 1 Family life nâng cao
-
20 bộ đề thi học kì 1 Toán 11
-
Bài tập cuối tuần môn Toán lớp 6 Cánh diều - Tuần 1
-
Bảng công thức lượng giác dùng cho lớp 10 - 11 - 12
-
TOP 13 Viết thư cho ông bà để hỏi thăm và kể về tình hình gia đình em lớp 4
-
Được 18-20 điểm khối A1 nên đăng ký trường nào?
-
Bài tập xác suất lớp 11 có đáp án
Từ khóa » Bài Tập ôn Thi Hk1 Toán 11
-
Đề ôn Tập Học Kì 1 Toán Lớp 11 Có đáp án Và Lời Giải Chi Tiết
-
Đề Thi HK1 Toán 11
-
Đề Cương ôn Thi Học Kì 1 Môn Toán Lớp 11 Năm 2021
-
180 Đề Thi Học Kì 1 Lớp 11 Môn Toán – Có Hướng Dẫn Giải Và đáp án
-
Ôn Tập Học Kì 1 - Toán 11 - Thầy Nguyễn Văn Đức - YouTube
-
Ôn Tập HK1 - Môn Toán Lớp 11 - Thầy Giáo: Nguyễn Công Chính
-
Đề Kiểm Tra Học Kì 1 Toán 11 Mới Nhất Có Đáp Án - Kiến Guru
-
Đề Cương ôn Tập HK1 Toán Lớp 11 Cơ Bản Và Nâng Cao
-
Đề Cương ôn Tập Học Kì 1 Lớp 11 Môn Toán 2021
-
Đề Cương ôn Tập Học Kỳ 1 Toán 11 (đầy đủ) - MathVn.Com
-
Đề Thi Học Kì 1 Toán 11 - Hướng Dẫn Giải
-
[PDF] ĐỀ CƯƠNG ÔN THI HỌC KỲ 1 TOÁN 11
-
Đề Thi Cuối Kì 1 Toán 11
-
ĐÁP ÁN ĐỀ THI TOÁN 11-HK1 | THPT MARIE CURIE



























