Đề Số 11 - Đề Kiểm Tra Học Kì 1 - Toán 6
Có thể bạn quan tâm
Đề bài
I. Trắc nghiệm (2 điểm):
Câu 1 :Cho tập hợp M = {4; 13; 7; 25}. Cách viết nào sau đây là đúng?
A.\(14 \in M\)
B.\({\rm{\{ 13; 25\} }} \in {\rm{M}}\)
C.\(25 \notin M\)
D.\({\rm{\{ 4; 7\} }} \subset {\rm{M}}\)
Câu 2 : Kết quả của phép tính: \({7^6}:{7^2}\) là:
A.\({49^3}\) B. 1
C.\({7^4}\) D.\({7^8}\)
Câu 3 : Kết quả phân tích ra thừa số nguyên tố nào sau đây là đúng.
A.\(84 = {2^2}.21\)
B.\(340 = {2^3}.5.17\)
C.\(92 = 2.46\)
D.\(228 = {2^2}.3.19\)
Câu 4 : ƯCLN(126; 144) là:
A.6 B.10
C.15 D.18
Câu 5 : Tập hợp nào chỉ gồm các số nguyên tố:
A.{3; 5; 7; 11}
B.{3; 10; 7; 13}
C. {13; 15; 17; 19}
D. {1; 2; 5; 7}
Câu 6 : Cho biết –12 + x = 3. Giá trị của x là
A.x = 9 B. x = 15
C.x = –15 D.x = –9
Câu 7 : Cho ba điểm D, H, G thẳng hàng. Nếu DG + HG = DH thì:
A.D nằm giữa H và G
B.G nằm giữa D và H
C.H nằm giữa D và G
D.Một kết quả khác
Câu 8 : Cho hình vẽ. Khi đó:
A.Hai tia Ax, By đối nhau
B. Hai tia AB, BA đối nhau
C. Hai tia Ay, AB đối nhau
D. Hai tia By, Bx đối nhau

II. Tự luận (8 điểm)
Bài 1: Thực hiện phép tính (Tính nhanh nếu có thể)
a) 18.25 + 75.18 – 1200
b) \({6^7}:{6^5} + {3.3^2} - {2017^0}\)
c) \({\rm{\{ [}}(20 - 2.3).5{\rm{]}} + 2 - 2.6\} \,\,:\,\,2\, + \,{(4.5)^2}\)
Bài 2: Tìm x, biết:
a) x + 7 = –23 + 5
b) \({2^{x + 1}} - 8 = 8\)
c) \((4x - 16):{3^2} = 4\)
Bài 3:Một trường có khoảng 700 đến 800 học sinh. Tính số học sinh của trường, biết rằng khi xếp hàng 40 học sinh hay 45 học sinh đều thừa 3 người.
Bài 4: Trên tia Ax, vẽ hai điểm M và N sao cho AM = 3cm; AN = 5cm.
a) Tính độ dài MN.
b) Gọi I là trung điểm của MN. Tính độ dài đoạn thẳng MI.
c) Vẽ tia Ay là tia đối của tia Ax. Trên tia Ay xác định điểm H sao cho AH = 3cm. Chứng tỏ A là trung điểm của đoạn thẳng HM.
Bài 5: Tìm số tự nhiên n để \((3n + 5)\,\, \vdots \,\,(n + 1)\)
Lời giải chi tiết
I. Trắc nghiệm (2 điểm)
| 1D | 2C | 3D | 4D |
| 5A | 6B | 7B | 8D |
II. Tự luận
Bài 1
\(\begin{array}{l}a)\,18.25 + 75.18 - 1200\\\,\,\,\, = 18.(25 + 75) - 1200\\\,\,\,\, = 18.100 - 1200\\\,\,\,\, = 1800 - 1200\\\,\,\,\, = \,\,600\\{\rm{c)}}\,{\rm{\{ [}}(20 - 2.3).5{\rm{]}} + 2 - 2.6\} \,\,:\,\,2\, + \,{(4.5)^2}\\\,\,\, = {\rm{\{ [}}(20 - 6).5{\rm{]}} + 2 - 12\} \,\,:\,\,2\, + \,{20^2}\\\,\,\, = {\rm{\{ [14}}.5{\rm{]}} + 2 - 12\} \,\,:\,\,2\, + \,400\\\,\,\, = \,{\rm{\{ 70 + 2}} - {\rm{12\} :}}\,\,{\rm{2 + }}\,\,{\rm{400}}\\\,\,\,{\rm{ = }}\,\,{\rm{(72}} - {\rm{12\} :}}\,\,{\rm{2 + }}\,\,{\rm{400}}\\\,\,\,{\rm{ = }}\,\,{\rm{60}}\,\,{\rm{:}}\,\,{\rm{2}}\,\,{\rm{ + }}\,\,{\rm{400}}\\\,\,\,{\rm{ = 30}}\,\,{\rm{ + }}\,\,{\rm{400}}\\\,\,\,{\rm{ = 430}}\end{array}\)
\(b)\,{6^7}:{6^5} + {3.3^2} - {2017^0}\)
\(={6^2} + {3^3} - 1\)
\(= \,\,36\, + 27 - 1\)
\(= \,\,\,63 - 1\)
\(=62\)
Bài 2
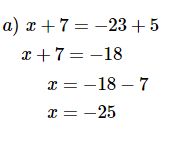
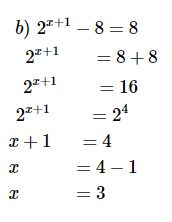
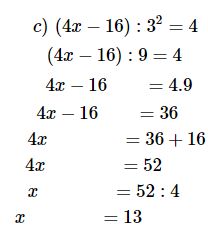
Bài 3
Gọi x (học sinh) là số học sinh của trường \(\left( {700 < x < 800,\;\;x \in N} \right).\)
Vì khi xếp hàng 40 học sinh hay 45 học sinh đều thừa 3 người nên suy ra \((x - 3)\,\, \vdots \,\,40\,\,;\,\,\,(x - 3)\,\, \vdots \,\,45\), hay \(x - 3 \in BC\,(40;\,\,45)\)
Ta có: \(40\, = {2^3}.5\,\,\,;\,\,\,\,\,45 = {3^2}.5\).
\(\begin{array}{l}BCNN(40;45) = {2^3}{.3^2}.5 = 360\\BC\left( {40;\;45} \right) = B\left( {360} \right) = \left\{ {0;\;360;\;720;\;1080;....} \right\}\end{array}\).
Do đó: \(x - 3 \in \left\{ {0\,;\,\,360\,;\,\,720\,;\,\,1080;\,\,...} \right\}\)
Suy ra \(x \in \left\{ {3\,;\,\,363\,;\,\,723\,;\,\,1083;\,\,...} \right\}\)
Lại có \(700 < x < 800\) nên \(x = 723.\)
Vậy trường đó có 723 học sinh.
Bài 4

a) Trên tia Ax ta có \(AM < AN\;\left( {do\;3cm\; < \;5cm} \right)\)nên điểm M nằm giữa hai điểm A và N.
\(\begin{array}{l} \Rightarrow AM + MN = AN\\ \Rightarrow MN = AN - AM = 5 - 3 = 2cm\end{array}\)
b) Vì I là trung điểm của MN nên \(MI = IN = \dfrac{1}{2}MN\,\,\,\)
\( \Rightarrow \,\,\,MI = 2:\,\,2 = 1cm\).
c) Ta có điểm H thuộc tia Ay, điểm M thuộc tia Ax và tia Ay là tia đối của tia Ax nên A là điểm nằm giữa hai điểm H và M.
Lại có AH = AM = 3cm.
Suy ra điểm A là trung điểm của đoạn thẳng HM.
Bài 5
Ta có : \(3n + 5 = 3n + 3 + 2 = 3\left( {n + 1} \right) + 2.\)
Khi đó ta có: \((3n + 5):(n + 1) = \dfrac{{3.(n + 1)}}{{n + 1}} + \dfrac{2}{{n + 1}} = 3 + \dfrac{2}{{n + 1}}\).
Để \(3n + 5\) chia hết cho \(n + 1\) thì 2 phải chia hết cho \(n + 1\), suy ra \(n + 1 \in U\left( 2 \right).\)
Lại có: \(U\left( 2 \right) = \left\{ { - 2; - 1;\;1;\;2} \right\}.\)
Ta có bảng sau:
| n + 1 | –2 | –1 | 1 | 2 |
| n | –3 | –2 | 0 | 1 |
Vì n là số tự nhiên nên \(n \in {\rm{\{ 0;}}\,\,1{\rm{\} }}\).Vậy để \(3n + 5\) chia hết cho \(n + 1\) thì \(n \in {\rm{\{ 0}}\,{\rm{;}}\,\,{\rm{1\} }}\).
Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 6 tại Tuyensinh247.com
Loigiaihay.com
Từ khóa » Tính Nhanh Lớp 6 Học Kì 2
-
Tham Khảo 2 Đề Toán 6 Học Kì 2 Hay Nhất Năm Học 2015 – 2016
-
Các Bài Toán Tính Nhanh Lớp 6 - Trọn Bộ Bài Luyện Tập Tính Nhanh
-
Một Số Bài Toán Tính Nhanh Lớp 6 - Học Toán 123
-
Đề Thi Học Kì 2 Toán 6 Sách Mới Năm 2022
-
Một Số Bài Toán Tính Nhanh Và Tìm X Lớp 6 - Abcdonline
-
Lớp 6 - Ôn Tập Học Kì II -Thực Hiện Phép Tính - Cô Bùi Thanh Bình
-
Các Dạng Toán Lớp 6 Học Kì 2 Hay Nhất - TopLoigiai
-
Các Bài Toán Tính Nhanh Nâng Cao Lớp 6 Hay Nhất - TopLoigiai
-
Đề ôn Tập Học Kì 2 Môn Toán Lớp 6 - Luyện Tập Đại Số Và Hình Học ...
-
Tuyển Tập Các Bài Toán Nâng Cao Lớp 6 Học Kì 2 Có đáp án
-
Top 8 Các Bài Toán Tính Nhanh Lớp 6 Có đáp An 2022
-
Đề Thi Giữa Học Kì 1 Môn Toán Lớp 6 Năm 2019 - 2020 - Đề 2