Đề Thi Giữa Kì 1 Toán 9 Năm Học 2020 - 2021 - Đề 2

Có thể bạn quan tâm

Đề thi giữa kì 1 Toán 9 năm 2023 - Đề 2 Đề kiểm tra giữa kì 1 Toán 9 có đáp án Bài trước Tải về Bài sau Lớp: Lớp 9 Môn: Toán Dạng tài liệu: Đề thi Loại: Tài liệu Lẻ Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Đề kiểm tra giữa kì 1 Toán 9 năm học 2022 - 2023

Đề thi giữa học kì 1 Toán 9 – Đề số 2
Đáp án đề kiểm tra giữa kì 1 Toán 9 – Đề số 2

Mời các bạn tham khảo Đề thi giữa kì 1 lớp 9 môn Toán năm 2023 được VnDoc biên soạn và đăng tải sau đây. Đề thi giữa kì Toán 9 này kèm theo đáp án sẽ là tài liệu hay cho các em học sinh ôn luyện trước kì thi, chuẩn bị cho kì thi sắp tới đạt kết quả cao. Dưới đây là nội dung chi tiết đề thi, các em tham khảo nhé.

Xem thêm: Đề kiểm tra giữa học kì 1 môn Toán lớp 9 Đề 1

Đề thi giữa học kì 1 Toán 9 – Đề số 2

Bài 1 (1 điểm): Tìm điều kiện để các căn thức dưới đây có nghĩa:

a) $\sqrt {16 - 4x}$ $\sqrt {16 - 4x}$

b) $\sqrt {3x + 7}$ $\sqrt {3x + 7}$

Bài 2 (2 điểm): Rút gọn các biểu thức dưới đây:

a) $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$ $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$

b) $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}}$ $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}}$

Bài 3 (2 điểm): Cho hai biểu thức $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$ $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$và $N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$ $N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$

a) Rút gọn biểu thức P = M:N

b) Tính giá trị của biểu thức P tại $x = 4 - 2\sqrt 3$ $x = 4 - 2\sqrt 3$

Bài 4 (2 điểm): Giải phương trình:

a) ${x^2} - 8x - 9 = 0$ ${x^2} - 8x - 9 = 0$

b) $\sqrt {5x + 4} = x + 2$ $\sqrt {5x + 4} = x + 2$

Bài 5 (3 điểm): Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm.

a) Chứng minh tam giác ABC là tam giác vuông.

b) Vẽ đường cao AH (H ∈ BC). Tính độ dài của BH, HC và AH.

c) Trên tia đối của tia BA, lấy điểm D sao cho BD = BC. Chứng minh: ${\mathop{\rm AD}\nolimits} .BC = \frac{{{{{\mathop{\rm CD}\nolimits} }^2}}}{2}$ ${\mathop{\rm AD}\nolimits} .BC = \frac{{{{{\mathop{\rm CD}\nolimits} }^2}}}{2}$

d) Tính diện tích tam giác BCD

Đáp án đề kiểm tra giữa kì 1 Toán 9 – Đề số 2

Bài 1:

a) Để biểu thức $\sqrt {16 - 4x}$ $\sqrt {16 - 4x}$ có nghĩa thì $16 - 4x \ge 0 \Leftrightarrow x \le 4$ $16 - 4x \ge 0 \Leftrightarrow x \le 4$

b) Để biểu thức $\sqrt {3x + 7}$ $\sqrt {3x + 7}$ có nghĩa thì $3x + 7 \ge 0 \Leftrightarrow x \ge \frac{{ - 7}}{3}$ $3x + 7 \ge 0 \Leftrightarrow x \ge \frac{{ - 7}}{3}$

Bài 2:

a) $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$ $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$

$A = \sqrt {36.2} - 2.\frac{1}{2} + \sqrt {16.2} + \sqrt {81.2}$ $A = \sqrt {36.2} - 2.\frac{1}{2} + \sqrt {16.2} + \sqrt {81.2}$

$A = 6\sqrt 2 - 1 + 4\sqrt 2 + 9\sqrt 2$ $A = 6\sqrt 2 - 1 + 4\sqrt 2 + 9\sqrt 2$

$A = 19\sqrt 2 - 1$ $A = 19\sqrt 2 - 1$

b) $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}} = \frac{{\sqrt 7 + 4 + \sqrt 7 - 4}}{{\left( {\sqrt 7 - 4} \right)\left( {\sqrt 7 + 4} \right)}} = \frac{{2\sqrt 7 }}{{7 - 16}} = \frac{{2\sqrt 7 }}{{ - 9}} = \frac{{ - 2\sqrt 7 }}{9}$ $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}} = \frac{{\sqrt 7 + 4 + \sqrt 7 - 4}}{{\left( {\sqrt 7 - 4} \right)\left( {\sqrt 7 + 4} \right)}} = \frac{{2\sqrt 7 }}{{7 - 16}} = \frac{{2\sqrt 7 }}{{ - 9}} = \frac{{ - 2\sqrt 7 }}{9}$

Bài 3:

a) $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$ $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$; điều kiện $x \ge 1$ $x \ge 1$

$M = \frac{{\sqrt x + \sqrt {x - 1} - \left( {\sqrt x - \sqrt {x - 1} } \right)}}{{\left( {\sqrt x - \sqrt {x - 1} } \right)\left( {\sqrt x + \sqrt {x - 1} } \right)}} = \frac{{2\sqrt {x - 1} }}{{x - \left( {x - 1} \right)}} = 2\sqrt {x - 1}$ $M = \frac{{\sqrt x + \sqrt {x - 1} - \left( {\sqrt x - \sqrt {x - 1} } \right)}}{{\left( {\sqrt x - \sqrt {x - 1} } \right)\left( {\sqrt x + \sqrt {x - 1} } \right)}} = \frac{{2\sqrt {x - 1} }}{{x - \left( {x - 1} \right)}} = 2\sqrt {x - 1}$

$N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$ $N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$; điều kiện $x \ge 0;x \ne 25$ $x \ge 0;x \ne 25$

$P = M:N = 2\sqrt {x - 1} .\frac{{\sqrt x - 5}}{{\sqrt {x - 1} }} = 2\left( {\sqrt x - 5} \right)$ $P = M:N = 2\sqrt {x - 1} .\frac{{\sqrt x - 5}}{{\sqrt {x - 1} }} = 2\left( {\sqrt x - 5} \right)$

Vậy $P = 2\left( {\sqrt x - 5} \right)$ $P = 2\left( {\sqrt x - 5} \right)$

b) Tại $x = 4 - 2\sqrt 3$ $x = 4 - 2\sqrt 3$(tm) thì $\sqrt x = \sqrt {4 - 2\sqrt 3 } = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} = \sqrt 3 - 1$ $\sqrt x = \sqrt {4 - 2\sqrt 3 } = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} = \sqrt 3 - 1$

Có $P = 2\left( {\sqrt 3 - 1 - 5} \right) = 2\left( {\sqrt 3 - 6} \right) = 2\sqrt 3 - 12$ $P = 2\left( {\sqrt 3 - 1 - 5} \right) = 2\left( {\sqrt 3 - 6} \right) = 2\sqrt 3 - 12$

Vậy tại $x = 4 - 2\sqrt 3$ $x = 4 - 2\sqrt 3$ thì $P = 2\sqrt 3 - 12$ $P = 2\sqrt 3 - 12$

Bài 4:

a) ${x^2} - 8x - 9 = 0$ ${x^2} - 8x - 9 = 0$

$\Leftrightarrow {x^2} + x - 9x - 9 = 0$ $\Leftrightarrow {x^2} + x - 9x - 9 = 0$

$\Leftrightarrow x\left( {x + 1} \right) - 9\left( {x + 1} \right) = 0$ $\Leftrightarrow x\left( {x + 1} \right) - 9\left( {x + 1} \right) = 0$

$\Leftrightarrow \left( {x - 9} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 9\\ x = - 1 \end{array} \right.$ $\Leftrightarrow \left( {x - 9} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 9\\ x = - 1 \end{array} \right.$

Vậy S = {-1; 9}

b) $\sqrt {5x + 4} = x + 2$ $\sqrt {5x + 4} = x + 2$(1)

Điều kiện $5x + 4 \ge 0 \Leftrightarrow x \ge \frac{{ - 4}}{5}$ $5x + 4 \ge 0 \Leftrightarrow x \ge \frac{{ - 4}}{5}$

(1) $\Leftrightarrow \left\{ \begin{array}{l} x + 2 \ge 0\\ 5x + 4 = {\left( {x + 2} \right)^2} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ 5x + 4 = {x^2} + 4x + 4 \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} x + 2 \ge 0\\ 5x + 4 = {\left( {x + 2} \right)^2} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ 5x + 4 = {x^2} + 4x + 4 \end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ {x^2} - x = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ \left[ \begin{array}{l} x = 0\\ x = 1 \end{array} \right.\left( {tm} \right) \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ {x^2} - x = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ \left[ \begin{array}{l} x = 0\\ x = 1 \end{array} \right.\left( {tm} \right) \end{array} \right.$

Vậy S = {0; 1}

Bài 4:

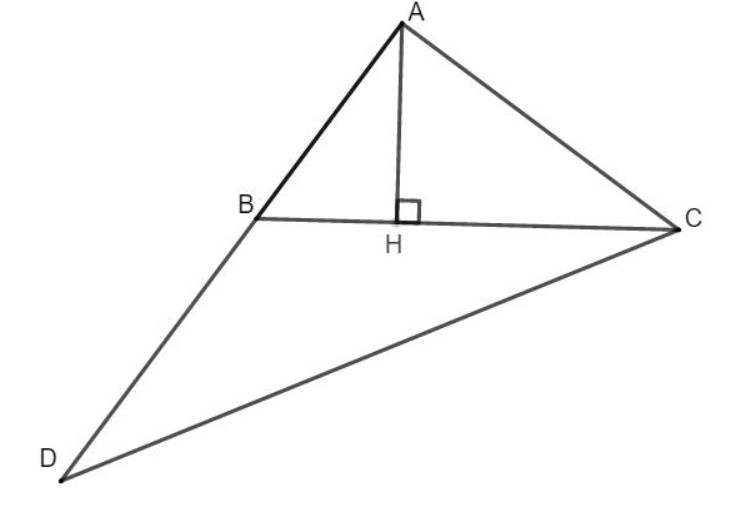
Đề thi giữa học kì 1 Toán 9 năm học 2020 - 2021 - Đề 2

a) Xét ∆ABC có:

$\left. \begin{array}{l} {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {6^2} + {8^2} = 100\\ {{\mathop{\rm BC}\nolimits} ^2} = {10^2} = 100 \end{array} \right\} \Rightarrow {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm BC}\nolimits} ^2}$ $\left. \begin{array}{l} {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {6^2} + {8^2} = 100\\ {{\mathop{\rm BC}\nolimits} ^2} = {10^2} = 100 \end{array} \right\} \Rightarrow {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm BC}\nolimits} ^2}$

⇒ABC vuông tại A (Pitago đảo)

b) Xét ∆ABC vuông tại A(cmt), có AH ⊥ BC:

+ ${{\mathop{\rm AB}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .BC$ ${{\mathop{\rm AB}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .BC$(hệ thức lượng trong tam giác vuông)

$\Rightarrow {\mathop{\rm BH}\nolimits} = \frac{{{{{\mathop{\rm AB}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{36}}{{100}} = \frac{9}{{25}}$ $\Rightarrow {\mathop{\rm BH}\nolimits} = \frac{{{{{\mathop{\rm AB}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{36}}{{100}} = \frac{9}{{25}}$(cm)

+ ${{\mathop{\rm AC}\nolimits} ^2} = {\mathop{\rm CH}\nolimits} .CB$ ${{\mathop{\rm AC}\nolimits} ^2} = {\mathop{\rm CH}\nolimits} .CB$(hệ thức lượng trong tam giác vuông)

$\Rightarrow {\mathop{\rm CH}\nolimits} = \frac{{{{{\mathop{\rm AC}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{64}}{{100}} = \frac{{16}}{{25}}$ $\Rightarrow {\mathop{\rm CH}\nolimits} = \frac{{{{{\mathop{\rm AC}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{64}}{{100}} = \frac{{16}}{{25}}$(cm)

+ ${{\mathop{\rm AH}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .HC$ ${{\mathop{\rm AH}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .HC$(hệ thức lượng trong tam giác vuông)

$\Rightarrow {{\mathop{\rm AB}\nolimits} ^2} = \frac{9}{{25}}.\frac{{16}}{{25}} \Rightarrow {\mathop{\rm AB}\nolimits} = \frac{{12}}{{25}}$ $\Rightarrow {{\mathop{\rm AB}\nolimits} ^2} = \frac{9}{{25}}.\frac{{16}}{{25}} \Rightarrow {\mathop{\rm AB}\nolimits} = \frac{{12}}{{25}}$(cm)

c) + Có AD = AB + BD = 6 + 10 = 16 (cm)

+ Xét ∆ADC vuông tại A có:

${{\mathop{\rm AD}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm CD}\nolimits} ^2}$ ${{\mathop{\rm AD}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm CD}\nolimits} ^2}$(Pitago)

$\Rightarrow {\mathop{\rm CD}\nolimits} = \sqrt {{{16}^2} + {8^2}} = 8\sqrt 5$ $\Rightarrow {\mathop{\rm CD}\nolimits} = \sqrt {{{16}^2} + {8^2}} = 8\sqrt 5$(cm)

+ Có AD.BC = 16.10 = 160

Và $\frac{{C{D^2}}}{2} = \frac{{320}}{2} = 160$ $\frac{{C{D^2}}}{2} = \frac{{320}}{2} = 160$

Vậy ${\mathop{\rm AD}\nolimits} .BC = \frac{{C{D^2}}}{2}$ ${\mathop{\rm AD}\nolimits} .BC = \frac{{C{D^2}}}{2}$

d) + ${{\mathop{\rm S}\nolimits} _{\Delta ABC}} = \frac{1}{2}{\mathop{\rm AB}\nolimits} .AC = \frac{1}{2}.6.8 = 24$ ${{\mathop{\rm S}\nolimits} _{\Delta ABC}} = \frac{1}{2}{\mathop{\rm AB}\nolimits} .AC = \frac{1}{2}.6.8 = 24$ (cm2)

+ ${{\mathop{\rm S}\nolimits} _{\Delta {\mathop{\rm ACD}\nolimits} }} = \frac{1}{2}{\mathop{\rm A}\nolimits} {\mathop{\rm D}\nolimits} .AC = \frac{1}{2}.16.8 = 64$ ${{\mathop{\rm S}\nolimits} _{\Delta {\mathop{\rm ACD}\nolimits} }} = \frac{1}{2}{\mathop{\rm A}\nolimits} {\mathop{\rm D}\nolimits} .AC = \frac{1}{2}.16.8 = 64$(cm2)

Vậy S∆BCD = 64 – 24 = 40 (cm2)

...........................

Để tham khảo thêm các đề thi khác, mời các bạn vào chuyên mục Đề thi giữa kì 1 lớp 9 với đầy đủ các môn, giúp các em ôn luyện trước kì thi, đồng thời cũng là tài liệu hay cho thầy cô tham khảo ra đề.

Từ khóa » đề Thi Giữa Kì Toán 9 2021

Đề Thi Giữa Kì 1 Toán 9 Năm Học 2020 - 2021 - Đề 2

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Đề kiểm tra giữa kì 1 Toán 9 năm học 2022 - 2023

Đề thi giữa học kì 1 Toán 9 – Đề số 2

Đáp án đề kiểm tra giữa kì 1 Toán 9 – Đề số 2

TOP 3 Đề Thi Giữa Kì 1 Toán 9 Năm 2021 - 2022 (Có Ma Trận, đáp án)

Đề Thi Giữa Kì 2 Toán 9 Năm 2021 - 2022 (7 Đề)

Đề Thi Giữa HK1 Toán 9 - Toán THCS

[Năm 2021] Đề Thi Giữa Kì 1 Toán Lớp 9 Có đáp án (10 đề)

Đề Thi Giữa Học Kì 1 Lớp 9 Môn Toán Mới Nhất

Đề Thi Giữa Kì 2 Toán 9 Năm Học 2021 - 2022 Đề 1

Đề Thi Giữa Kì 1 Toán 9 Năm 2021 - 2022 (đề 8)

Top 12 Đề Kiểm Tra Giữa Kì Toán 9

Đề Thi Giữa Học Kì 1 Lớp 9 Năm 2021 - 2022 - Tuyensinh247

Top 12 Đề Toán Giữa Kì 1 Lớp 9

Top 29 đề Thi Giữa Kì Môn Toán Lớp 9 2022

Đề Thi Giữa Học Kì 1 Lớp 9 Môn Toán Năm 2021-2022

Đề Thi Giữa Kì 1 Lớp 9 Chọn Lọc Có đáp án Mới Nhất

ĐỀ THI GIỮA HỌC KÌ 1 MÔN TOÁN LỚP 9 NĂM HỌC 2021-2022

Toán Học Lớp 9 - Đề Thi Giữa HK2 - Năm Học 2021 - 2022 - YouTube

Đề Thi Giữa Kì 1 Toán 9 Năm 2020 – 2021 Trường THCS Đống Đa

Toán Lớp 9 Tập 1: Tuyển Tập Bộ đề Thi Giữa Kì 1 Các Trường THCS Hà ...

Liên Hệ