Đề Thi Học Kì 1 Môn Toán Lớp 7 Năm 2019

Bài 1  (2 điểm) Thực hiện từng bước phép tính :

a) \(\sqrt {\dfrac{9}{{16}}}  - 0,\left( 3 \right) - \left( { - \dfrac{2}{9}} \right) + \dfrac{1}{{2019}} - \dfrac{3}{5} \)\(+ {\left( {\dfrac{1}{6}} \right)^2} + \dfrac{{ - 1}}{{15}}\)

b) \(\dfrac{{ - {{22}^{33}}{{.33}^{55}}.{{\left( { - 55} \right)}^{22}}}}{{{{\left( { - 6} \right)}^{33}}.{{\left( { - 15} \right)}^{22}}{{.11}^{111}}}}\)

Bài 2 (1,5 điểm): Tìm \(x\) biết :

a) \(\left| {3 - 2x} \right| + \sqrt {\dfrac{9}{{25}}}  = \sqrt {\dfrac{{16}}{{25}}} \)

b) \(\dfrac{{2x - 1}}{{ - 2}} = \dfrac{{ - 50}}{{2x - 1}}\,\,\,\left( {x \ne \dfrac{1}{2}} \right)\)

Bài 3 (2 điểm): Có \(3\) gói tiền: gói thứ nhất gồm toàn tờ bạc \(20000\) đồng, gói thứ hai gồm toàn tờ bạc \(50000\) đồng, gói thứ ba gồm toàn tờ bạc \(100000\) đồng. Biết số tiền ở ba gói bằng nhau và gói thứ nhất hơn gói thứ ba \(68\) tờ giấy bạc. Hỏi mỗi loại có bao nhiêu tờ giấy bạc và tổng số tiền ở cả ba gói là bao nhiêu ?

Bài 4 (1 điểm):

a)Vẽ đồ thị hàm số \(y = \dfrac{3}{2}x\).

b) Cho \(A\left( {12;18} \right)\) và \(B\left( {20;25} \right)\). Hỏi đồ thị của hàm số trên đi qua điểm nào trong hai điểm đã cho? Giải thích?

Bài 5 (3,5 điểm): Cho tam giác \(ABC\) vuông tại \(A\left( {AB < AC} \right).\) Tia \(BD\) là tia phân giác của \(\widehat {ABC}\left( {D \in AC} \right)\). Trên cạnh \(BC,\) lấy điểm \(E\) sao cho \(BE = BA.\)

a) Chứng minh : \(\Delta ABD = \Delta EBD\) và \(DE \bot BC.\)

b) \(BA\) và \(ED\) cắt nhau tại \(F.\) Chứng minh : \(\Delta DAF = \Delta DEC\) và \(BF = BC.\)

c) Gọi \(H\) là giao điểm của \(BD\) và \(FC.\) Chứng minh : \(BH\) là đường trung trực của đoạn thẳng \(FC.\)

d) Gọi \(M\) là trung điểm của \(EC.\) Trên tia đối của tia \(MF\) lấy điểm \(K\) sao cho \(MK = MF.\)

Chứng minh : ba điểm \(A,\,E,\,K\) thẳng hàng.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

Bài 1 (VD):

Phương pháp:

Sử dụng kiến thức về căn bậc hai.

Qui ước \({a^0} = 1.\)

Và \({\left( {{a^m}} \right)^n} = {a^{m.n}};\,\dfrac{{{a^m}}}{{{a^n}}} = {a^{m - n}}\) 

Cách giải:

a) \(\sqrt {\dfrac{9}{{16}}}  - 0,\left( 3 \right) - \left( { - \dfrac{2}{9}} \right) + \dfrac{1}{{2019}} \)\(- \dfrac{3}{5} + {\left( {\dfrac{1}{6}} \right)^2} + \dfrac{{ - 1}}{{15}}\)

\(= \sqrt {\dfrac{9}{{16}}}  - 3 \cdot 0,\left( 1 \right) + \dfrac{2}{9} + \dfrac{1}{{2019}} \)\( - \dfrac{3}{5} + \dfrac{1}{{36}} - \dfrac{1}{{15}}\)

\(= \dfrac{3}{4} - 3 \cdot \dfrac{1}{9} + \dfrac{2}{9} + \dfrac{1}{{2019}} - \dfrac{3}{5} \)\(+ \dfrac{1}{{36}} - \dfrac{1}{{15}}\)

\( = \dfrac{3}{4} - \dfrac{3}{9} + \dfrac{2}{9} + \dfrac{1}{{36}} - \left( {\dfrac{3}{5} + \dfrac{1}{{15}}} \right) \)\(+ \dfrac{1}{{2019}}\)

\(= \dfrac{3}{4} - \dfrac{1}{9} + \dfrac{1}{{36}} - \dfrac{{10}}{{15}} + \dfrac{1}{{2019}}\)

\(= \dfrac{{27 - 4 + 1}}{{36}} - \dfrac{2}{3} + \dfrac{1}{{2019}}\)

\(= \dfrac{2}{3} - \dfrac{2}{3} + \dfrac{1}{{2019}}\\ = \dfrac{1}{{2019}} \cdot\)  

b) \(\dfrac{{ - {{22}^{33}}{{.33}^{55}}.{{\left( { - 55} \right)}^{22}}}}{{{{\left( { - 6} \right)}^{33}}.{{\left( { - 15} \right)}^{22}}{{.11}^{111}}}}\)

\( = \dfrac{{ - {{22}^{33}}{{.33}^{55}}{{.55}^{22}}}}{{ - {6^{33}}{{.15}^{22}}{{.11}^{111}}}}\)

\(\begin{array}{l} = \dfrac{{ - {{1.2}^{33}}{{.11}^{33}}{{.3}^{55}}{{.11}^{55}}{{.5}^{22}}{{.11}^{22}}}}{{ - {{1.2}^{33}}{{.3}^{33}}{{.3}^{22}}{{.5}^{22}}{{.11}^{111}}}}\\ = \dfrac{{{2^{33}}{{.11}^{33 + 55 + 22}}{{.3}^{55}}{{.5}^{22}}}}{{{2^{33}}{{.3}^{33 + 22}}{{.5}^{22}}{{.11}^{111}}}}\\ = \dfrac{{{2^{33}}{{.11}^{110}}{{.3}^{55}}{{.5}^{22}}}}{{{2^{33}}{{.3}^{55}}{{.5}^{22}}{{.11}^{111}}}}\\ = \dfrac{1}{{11}}\end{array}\)

Bài 2 (VD):

Phương pháp:

Áp dụng các quy tắc chuyển vế đổi dấu và kiến thức về GTTĐ để tìm \(x\).

Cách giải:

a)  \(\left| {3 - 2x} \right| + \sqrt {\dfrac{9}{{25}}}  = \sqrt {\dfrac{{16}}{{25}}} \)

\(\begin{array}{l}\left| {3 - 2x} \right| + \dfrac{3}{5} = \dfrac{4}{5}\\\left| {3 - 2x} \right| = \dfrac{4}{5} - \dfrac{3}{5}\\\left| {3 - 2x} \right| = \dfrac{1}{5}\end{array}\)

TH1 :

\(\begin{array}{l}3 - 2x = \dfrac{1}{5}\\2x = 3 - \dfrac{1}{5}\\2x = \dfrac{{14}}{5}\\x = \dfrac{{14}}{5}:2\\x = \dfrac{7}{5}\end{array}\)

TH2 :

\(\begin{array}{l}3 - 2x =  - \dfrac{1}{5}\\2x = 3 + \dfrac{1}{5}\\2x = \dfrac{{16}}{5}\\x = \dfrac{{16}}{5}:2\\x = \dfrac{8}{5}\end{array}\)

Vậy \(x = \dfrac{7}{5}\) hoặc \(x = \dfrac{8}{5}\).

b) \(\dfrac{{2x - 1}}{{ - 2}} = \dfrac{{ - 50}}{{2x - 1}}\,\,\,\left( {x \ne \dfrac{1}{2}} \right)\)

\(\begin{array}{l}{\left( {2x - 1} \right)^2} =  - 2.\left( { - 50} \right)\\{\left( {2x - 1} \right)^2} = 100\end{array}\)

\(2x - 1 = 10\) hoặc \(2x - 1 =  - 10\)

TH1:

 \(\begin{array}{l}2x - 1 = 10\\2x = 10 + 1\\2x = 11\\x = \dfrac{{11}}{2}\end{array}\)

TH2:

\(\begin{array}{l}2x - 1 =  - 10\\2x =  - 10 + 1\\2x =  - 9\\x = \dfrac{{ - 9}}{2}\end{array}\)

Vậy \(x = \dfrac{{11}}{2}\) hoặc \(x =  - \dfrac{9}{2}\).

Bài 3 (VD):

Phương pháp:

- Gọi số tờ tiền của mỗi loại là \(a,b,c.\)

- Dựa vào đề bài, viết các tỉ lệ thức liên quan, áp dụng tính chất dãy tỉ số bằng nhau để tìm lời giải cho bài toán.

Cách giải:

Gọi số tờ tiền của mỗi loại giấy bạc \(20000\) đồng, \(50000\) đồng và \(100000\) đồng lần lượt là \(a,b,c\left( {a,b,c \in {\mathbb{N}^*},a > 68} \right)\)

Số tiền ở ba gói lần lượt là : \(20\,000a\) đồng; \(50000b\) đồng và \(100000c\) đồng.

Do số tiền ở ba gói là bằng nhau nên ta có : \(20000a = 50000b = 100000c\)

Chia cả ba vế cho \(100000\) ta được tỉ lệ thức:

\(\dfrac{a}{5} = \dfrac{b}{2} = \dfrac{c}{1}\)

Mà gói thứ nhất hơn gói thứ ba \(68\) tờ giấy bạc hay \(a - c = 68\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{a}{5} = \dfrac{b}{2} = \dfrac{c}{1} = \dfrac{{a - c}}{{5 - 1}} = \dfrac{{68}}{4} = 17\)

\( \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{5} = 17 \Rightarrow a = 17.5 = 85\\\dfrac{b}{2} = 17 \Rightarrow b = 17.2 = 34\\\dfrac{c}{1} = 17 \Rightarrow c = 17.1 = 17\end{array} \right.\)

Vậy có \(85\) tờ \(20000\) đồng, \(34\) tờ \(50000\) đồng và \(17\) tờ \(100000\) đồng.

Khi đó mỗi gói có số tiền là :

\(20000 \times 85 = 1700000\) (đồng)

Tổng số tiền ở cả ba gói là :

\(1700000 \times 3 = 5100000\) (đồng)

Bài 4 (VD):

Phương pháp:

a) Lấy hai điểm thuộc đồ thị hàm số :

- Cho \(x = 0\) tìm giá trị của \(y.\)

- Cho \(x = 1\) tìm giá trị tương ứng của \(y.\)

Nối hai điểm vừa tìm được, ta có đồ thị của hàm số.

b) Vận dụng kiến thức : Điểm \(A\left( {{x_A},{y_A}} \right)\) thuộc đồ thị của hàm số \(y = ax\) khi \({y_A} = a{x_A}.\)

Cách giải:

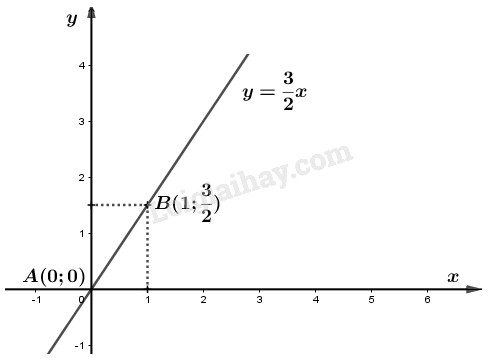
a)Vẽ đồ thị hàm số \(y = \dfrac{3}{2}x\)

Khi \(x = 0\) thì \(y = \dfrac{3}{2} \cdot 0 = 0\)

Khi \(x = 1\) thì \(y = \dfrac{3}{2} \cdot 1 = \dfrac{3}{2}\)

Vẽ đường thẳng đi qua hai điểm \(A\left( {0;0} \right);\,B\left( {1;\dfrac{3}{2}} \right)\), từ đó ta có đồ thị của hàm số \(y = \dfrac{3}{2}x\).

b) Cho \(A\left( {12;18} \right)\) và \(B\left( {20;25} \right)\). Hỏi đồ thị của hàm số trên đi qua điểm nào trong hai điểm đã cho? Giải thích?

Ta có :

\(18 = \dfrac{3}{2} \cdot 12\) nên điểm \(A\left( {12;18} \right)\) nằm trên đồ thị của hàm số \(y = \dfrac{3}{2}x\)

\(25 \ne \dfrac{3}{2} \cdot 20\) nên điểm \(B\left( {20;25} \right)\) không nằm trên đồ thị của hàm số \(y = \dfrac{3}{2}x\).

Bài 5 (VD):

Phương pháp:

- Nhớ lại kiến thức về các trường hợp bằng nhau của tam giác vuông rồi chứng minh.

Chú ý : Hai tam giác bằng nhau có các cặp cạnh và cặp góc tương ứng bằng nhau.

- Đường trung trực của một đoạn thẳng thì vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.

- Sử dụng tiên đề Ơclit chứng minh ba điểm thẳng hàng: Qua một điểm nằm ngoài đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

Cách giải:

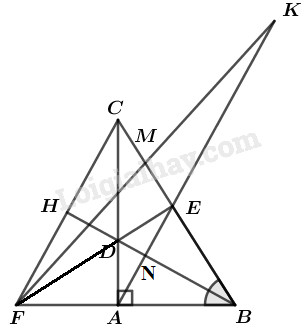
a) Chứng minh : \(\Delta ABD = \Delta EBD\) và \(DE \bot BC.\)

Xét \(\Delta ABD\) và \(\Delta EBD\) có

Cạnh \(BD\) chung.

\(\widehat {ABD} = \widehat {EBD}\) (\(BD\) là tia phân giác của góc \(B\))

\( \Rightarrow \Delta ABD = \Delta EBD\left( {ch - gn} \right)\)

\( \Rightarrow \widehat {DAB} = \widehat {DEB}\) (cặp góc tương ứng)

Mà \(\widehat {DAB} = 90^\circ \left( {gt} \right)\) nên \(\widehat {DEB} = 90^\circ \) hay \(DE \bot BC\)(đpcm)

b) \(BA\) và \(ED\) cắt nhau tại \(F.\) Chứng minh : \(\Delta DAF = \Delta DEC\) và \(BF = BC.\)

Từ câu a, \(\Delta ABD = \Delta EBD\)\( \Rightarrow DA = DE\) (cạnh tương ứng)

Xét hai tam giác vuông \(\Delta DAF\) và \(\Delta DEC\) ta có :

\(DA = DE\) (chứng minh trên)

\(\widehat {FDA} = \widehat {CDE}\) (cặp góc đối đỉnh)

\( \Rightarrow \Delta DAF = \Delta DEC\left( {gn - cgv} \right)\)

\( \Rightarrow AF = CE\) (cặp cạnh tương ứng)

Mà \(BA = BE\left( {gt} \right)\)

\( \Rightarrow AF + AB = CE + BE\) hay \(BF = BC.\)

c) Gọi \(H\) là giao điểm của \(BD\) và \(FC.\) Chứng minh : \(BH\) là đường trung trực của đoạn thẳng \(FC.\)

Xét tam giác \(BHC\) và \(BHF\) có :

\(BH\) là cạnh chung

\(\widehat {CBH} = \widehat {FBH}\left( {gt} \right)\)

\(BC = BF\left( {cmt} \right)\)

\( \Rightarrow \Delta BHC = \Delta BHF\left( {c - g - c} \right)\)

\( \Rightarrow CH = FH\) (cạnh tương ứng) (1)

\(\angle CHB = \angle FHB\) (góc tương ứng)

Mà \(\angle CHB + \angle FHB = {180^0}\) nên \(\angle CHB = \angle FHB = {90^0}\)\( \Rightarrow BH \bot CF\) (2)

Từ (1) và (2) suy ra \(BH\) là đường trung trực của đoạn thẳng \(CF\) (định nghĩa đường trung trực).

d) Gọi \(M\) là trung điểm của \(EC.\) Trên tia đối của tia \(MF\) lấy điểm \(K\) sao cho \(MK = MF.\)

Chứng minh : ba điểm \(A,\,E,\,K\) thẳng hàng.

Xét \(\Delta MCF\) và \(\Delta MEK\) có:

\(\begin{array}{l}MC = ME\left( {gt} \right)\\MK = MF\left( {gt} \right)\end{array}\)

\(\widehat {CMF} = \widehat {EMK}\) (đối đỉnh)

\( \Rightarrow \Delta MCF = \Delta MEK\left( {c - g - c} \right)\)

\( \Rightarrow \widehat {MKE} = \widehat {MFC}\) (góc tương ứng)

Mà hai góc này ở vị trí so le trong nên \(EK//CF\) (1)

Nối \(E\) với \(A\) cắt \(BD\) tại \(N\).

Xét \(\Delta ABN\) và \(\Delta EBN\) có:

\(\begin{array}{l}BA = BE\left( {gt} \right)\\\widehat {ABN} = \widehat {EBN}\left( {gt} \right)\\BN\,chung\end{array}\)

\( \Rightarrow \Delta ABN = \Delta EBN\left( {c - g - c} \right)\)

\( \Rightarrow \widehat {ANB} = \widehat {ENB}\) (góc tương ứng)

Mà \(\widehat {ANB} + \widehat {ENB} = {180^0}\) nên \(\widehat {ANB} = \widehat {ENB} = {90^0}\)\( \Rightarrow AE \bot BN\) hay \(AE \bot BH\)

Mà \(CF \bot BH\left( {cmt} \right)\) nên \(AE//CF\) (từ vuông góc đến song song)

Ta có: \(AE//CF,EK//CF\) nên theo tiên đề Ơ clit, có một và chỉ một đường thẳng đi qua \(E\) và song song \(CF\).

Vậy ba điểm \(A,E,K\) thẳng hàng (đpcm). 

HẾT

Loigiaihay.com