Đề Thi THPT Quốc Gia – NGUYỄN MINH HIẾU

Trang chủ » đề Toán 2018 Mã 101 Pdf » Đề Thi THPT Quốc Gia – NGUYỄN MINH HIẾU

Có thể bạn quan tâm

Skip to content

Tag: Đề Thi THPT Quốc Gia

Đề thi và lời giải chi tiết đề thi tốt nghiệp môn Toán 2022 của bộ Giáo dục và Đào tạo!

Đề thi và lời giải chi tiết để tham khảo tốt nghiệp môn Toán 2022 của bộ Giáo dục và Đào tạo!

Lời giải chi tiết đề thi Tốt nghiệp THPT 2021, môn Toán, khóa ngày 7/7/2021.

Mã đề 101

Click to access 2021made101-2.pdf

Mã đề 105

Click to access 2021made105-1.pdf

Tài liệu tổng hợp các đề thi (tham khảo và chính thức) của bộ GD và ĐT từ năm 2017 đến năm 2020. Các câu hỏi đều được phân dạng và sắp xếp từ dễ đến khó. Tài liệu bao gồm các câu hỏi với đáp án và lời giải chi tiết nhằm giúp học sinh tham khảo sau khi đã tự mình làm bài tập.

Click to access plchthptqg2017-2020-loigiai.pdf

Tài liệu tổng hợp các đề thi (tham khảo và chính thức) của bộ GD và ĐT từ năm 2017 đến năm 2020. Các câu hỏi đều được phân dạng và sắp xếp từ dễ đến khó. Tài liệu chỉ bao gồm các câu hỏi không có đáp án và lời giải nhằm giúp học sinh tự mình khám phá lời giải của riêng mình!

Click to access plchthptqg2017-2020-de.pdf

Câu 36 Có bao nhiêu giá trị nguyên của tham số m để hàm số y=x^8+(m-2)x^5-(m^2-4)x^4+1 đạt cực tiểu tại x=0? A. 3. B. 5. C. 4. D. Vô số.

Lời giải

Chọn phương án C.

Ta có y'=8x^7+5(m-2)x^4-4(m^2-4)x^3=x^3\left( 8x^4+5(m-2)x-4(m^2-4) \right) .

Đặt f(x)=8x^4+5(m-2)x-4(m^2-4), ta xét hai trường hợp:

• TH1: f(0)=0\Leftrightarrow m^2-4=0\Leftrightarrow m=\pm 2.

Với m=2\Rightarrow y'=8x^7\Rightarrow x=0 là điểm cực tiểu.

Với m=-2\Rightarrow y'=x^4\left( 8x^4-20\right) \Rightarrow x=0 không phải là điểm cực tiểu.

• TH2: f(0)\neq 0\Leftrightarrow m^2-4\neq 0\Leftrightarrow m\neq \pm 2.

Hàm số đạt cực tiểu tại x=0 khi và chỉ khi y'=x^3.f(x) đổi dấu từ - qua + khi qua x=0.

Điều này tương đương với \lim\limits_{x\to 0}f(x)>0\Leftrightarrow m^2-4<0\Leftrightarrow -2<m<2.

Kết hợp ta có bốn giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Câu 37 Cho hình lập phương ABCD. A'B'C'D' có tâm O. Gọi I là tâm hình vuông A'B'C'D' và M là điểm thuộc đoạn thẳng OI sao cho MO=2MI (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng (MC'D') và (MAB) bằng

Hinh37a

A. \dfrac{6\sqrt{85}}{85}. B. \dfrac{7\sqrt{85}}{85}. C. \dfrac{17\sqrt{13}}{65}. D. \dfrac{6\sqrt{13}}{65}.

Lời giải Chọn phương án B.

Hinh37b

Gọi P,Q lần lượt là trung điểm của D'C' và AB.

Ta có \begin{cases} MP\perp C'D' \parallel AB\\ MQ\perp AB \end{cases}\Rightarrow AB\perp (MPQ).

Suy ra (MAB)\perp (MPQ) và (MC'D')\perp (MPQ).

Do đó góc giữa (MAB) và (MC'D') bằng góc giữa MQ và MP.

Đặt AB=a, ta có OI=\dfrac{a}{2}\Rightarrow MI=\dfrac{1}{3}OI=\dfrac{a}{6}.

Gọi K là tâm của ABCD, ta có MK=IK-MI=\dfrac{5a}{6}.

Suy ra MP=\sqrt{MI^2+IP^2}=\dfrac{\sqrt{10}a}{6}, MQ=\sqrt{MK^2+KQ^2}=\dfrac{\sqrt{34}a}{6}, PQ=\sqrt{2}a.

Vậy \cos\alpha=|\cos \widehat{PMQ}|=\dfrac{\left|MP^2+MQ^2-PQ^2\right|}{2MP.MQ}=\dfrac{7\sqrt{85}}{85}.

Câu 42 Cho khối lăng trụ ABC. A'B'C', khoảng cách từ C đến đường thẳng BB' bằng 2, khoảng cách từ A đến các đường thẳng BB' và CC' lần lượt bằng 1 và \sqrt{3}, hình chiếu vuông góc của A lên mặt phẳng \left(A'B'C'\right) là trung điểm M của B'C' và A'M=\dfrac{2\sqrt{3}}{3}. Thể tích của khối lăng trụ đã cho bằng A. 2. B. 1. C. \sqrt{3}. D. \dfrac{2\sqrt{3}}{3}.

Lời giải

Chọn phương án A.

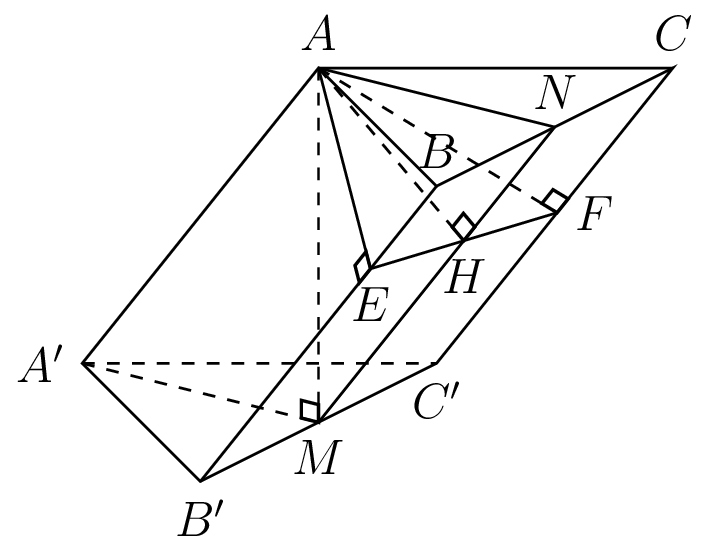
Hinh42b

Gọi E, F là hình chiếu của A trên BB' và CC'.

Ta có \begin{cases} AE\perp AA'\\ AF\perp AA' \end{cases}\Rightarrow AA'\perp (AEF)\Rightarrow BB'\perp EF.

Từ đó suy ra EF=d(F,BB')=d(C,BB')=2\Rightarrow \triangle AEF vuông tại A.

Gọi N trung điểm BC và H=MN\cap EF, ta có AH=\dfrac{1}{2}EF=1.

Dễ thấy \triangle AMN vuông tại A và có đường cao AH.

Do đó \dfrac{1}{AM^2}=\dfrac{1}{AH^2}-\dfrac{1}{AN^2}=\dfrac{1}{4}\Rightarrow AM=2.

Lại có MN=\sqrt{AM^2+AN^2}=\dfrac{4}{\sqrt{3}}\Rightarrow S_{BCC'B'}=MN.EF=\dfrac{8}{\sqrt{3}}.

Vậy V_{ABC.A'B'C'}=3V_{ABCC'}=\dfrac{3}{2}V_{A.BCC'B'}=\dfrac{1}{2}S_{BCC'B'}.\mathrm{d}(A,EF)=\dfrac{1}{2}.\dfrac{8}{\sqrt{3}}.\dfrac{\sqrt{3}}{2}=2.

Câu 43 Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1;17]. Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng A. \dfrac{1728}{4913}. B. \dfrac{1079}{4913}. C. \dfrac{23}{68}. D. \dfrac{1637}{4913}.

Lời giải

Chọn phương án D.

Mỗi bạn có 17 khả năng viết số nên số phần tử không gian mẫu là 17^3=4913.

Ta chia các số tự nhiên từ 1 đến 17 thành 3 nhóm: Nhóm I gồm các số chia hết cho 3 có 5 số; nhóm II gồm các số chia cho 3 dư 1 gồm 6 số; nhóm III gồm các số chia cho 3 dư 2 có 6 số.

Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên có tổng chia hết cho 3 gồm các trường hợp sau:

• TH1: Ba số đều chia hết cho 3 có 5^3=125 cách.

• TH2: Ba số đều chia cho 3 dư 1 có 6^3=216 cách.

• TH3: Ba số đều chia cho 3 dư 2 có 6^3=216 cách.

• TH4: Một số chia hết cho 3, một số chia cho 3 dư 1 và một số chia cho 3 dư 2 có 5.6.6.3!=1080 cách.

Từ đó suy ra số cách viết thỏa mãn yêu cầu bài toán là 125+216+216+1080=1637.

Vậy xác suất cần tìm là \dfrac{1637}{4913}.

Câu 50

Cho hai hàm số y=f(x), y=g(x). Hai hàm số y=f'(x) và y=g'(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=g'(x). Hàm số h(x)=f(x+4)-g\left(2x-\dfrac{3}{2}\right) đồng biến trên khoảng nào dưới đây?

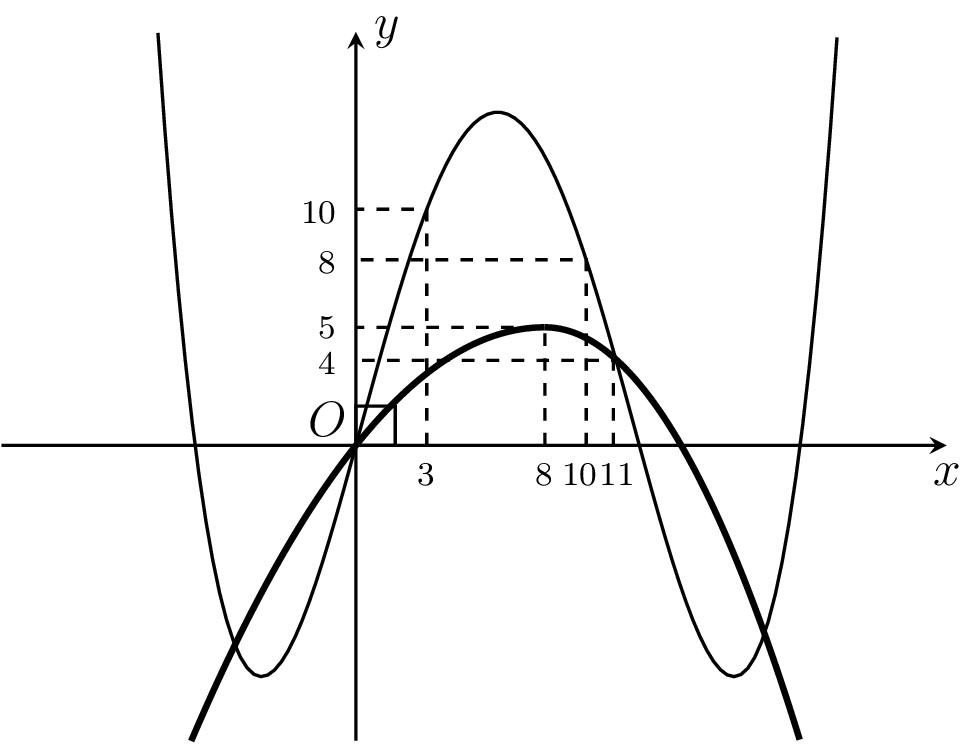Hinh50a A. \left(5;\dfrac{31}{5}\right). B. \left(\dfrac{9}{4};3\right). C. \left(\dfrac{31}{5};+\infty \right). D. \left(6;\dfrac{25}{4}\right).

Lời giải

Chọn phương án B.

Ta có h'(x)=f'(x+4)-2g'\left(2x-\dfrac{3}{2}\right).

Xét x=6,1, ta có h'(6,1)=f'(10,1)-2g'(10,7); từ đồ thị ta có f'(10,1)<f'(10)=8 và 2g'(10,7)>2g'(11)=8\Rightarrow h'(6,1)<0 nên loại phương án A và D.

Xét x=6,25, ta có h'(6,25)=f'(10,25)-2g'(11); từ đồ thị ta có f'(10,25)<f'(10)=8 và 2g'(1)=8\Rightarrow h'(6,25)<0 nên loại phương án C.

Tải về đề thi theo liên kết sau: 2018.Made101; Tải về hướng dẫn giải chi tiết đầy đủ theo liên kết sau: 2018.Made101.DA.

TẢI VỀ HƯỚNG DẪN GIẢI CHI TIẾT

TẢI VỀ ĐỀ THI VÀ ĐÁP ÁN

TẢI VỀ HƯỚNG DẪN GIẢI

TẢI VỀ ĐỀ THI VÀ ĐÁP ÁN

Lượt truy cập

  • 1,570,578 hits

BÀI VIẾT MỚI

  • Đề thi tốt nghiệp môn Toán 2022
  • Đề tham khảo tốt nghiệp môn Toán 2022
  • Giải chi tiết đề thi Tốt nghiệp THPT 2021, môn Toán, mã đề 101 và 105
  • Phân loại câu hỏi trong các đề thi THPTQG của Bộ GD và ĐT (lời giải)
  • Phân loại câu hỏi trong các đề thi THPTQG của Bộ GD và ĐT
  • Giải chi tiết đề thi THPT Quốc Gia 2018, mã đề 101 môn Toán
  • Định lý Ceva và ứng dụng
  • Giải chi tiết đề thi thử môn Toán năm 2018 trường THPT Đặng Thức Hứa lần 1
  • Giải chi tiết đề thi thử môn Toán năm 2018 Sở Giáo dục và Đào tạo Bắc Giang lần 1
  • Giải chi tiết đề thi thử môn Toán năm 2018 Sở Giáo dục và Đào tạo Nam Định lần 2

Bài viết phổ biến

  • Tích phân của hàm số chứa dấu giá trị tuyệt đối
  • Giải chi tiết đề tham khảo 2018 môn Toán của Bộ GD và ĐT
  • Điều Kiện Để Hàm Số Đơn Điệu Trên Một Khoảng Cho Trước
  • Cài đặt LaTeX trên Windows
  • Vẽ đồ thị hàm số trên LaTeX bằng METAPOST
  • Mẫu soạn đáp án đề thi đại học bằng LaTeX
  • Tạp chí Epsilon
  • Soạn Đề Thi Trắc Nghiệm Bằng LaTeX

THẺ

Các Nhà Toán Học Hình Học Phẳng Hệ Phương Trình Khảo Sát Hàm Số LaTeX METAPOST Nhị Thức Newton Toán Lớp 10 Toán Lớp 11 Toán Lớp 12 Toán Thi THPT Quốc Gia Tích Phân Tạp Chí Toán Học Tổ Hợp Xác Suất Đề Minh Họa THPTQG Đề Thi Cao Học Đề Thi Học Sinh Giỏi Tỉnh Đề Thi THPT Quốc Gia Đề Thi Thử THPTQG

  • Subscribe Subscribed
    • NGUYỄN MINH HIẾU
      • Join 74 other subscribers Sign me up
    • Already have a WordPress.com account? Log in now.
    • NGUYỄN MINH HIẾU
    • Subscribe Subscribed
    • Sign up
    • Log in
    • Report this content
    • View site in Reader
    • Manage subscriptions
    • Collapse this bar
Loading Comments... Write a Comment... Email (Required) Name (Required) Website Design a site like this with WordPress.comGet started

Từ khóa » đề Toán 2018 Mã 101 Pdf