Đề Thi Thử Vào Lớp 10 Môn Toán đề Số 23

Có thể bạn quan tâm

Click vào đề thi

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Cho biểu thức A = 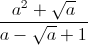$\frac{a^{2}+\sqrt{a}}{a-\sqrt{a}+1}$ - $\frac{2a+\sqrt{a}}{\sqrt{a}}$ + 1.

Câu 1: Rút gọn A.

Câu 2: Tìm giá trị nhỏ nhất của A.

Cho parabol (P) có đỉnh O(0; 0) và đi qua điểm (- 2; $\frac{4}{3}$ ).

Câu 3: Viết phương trình parabol (P) và vẽ parabol đó.

Câu 4: Viết phương trình đường thẳng cắt parabol (P) tại hai điểm lần lượt có hoành độ là 2 và – 1.

Câu 5: Tìm trên parabol (P) các điểm cách đều hai trục tọa độ.

Cho phương trình: x2 – mx – 4 = 0 (m là tham số).

Câu 6: Chứng minh rằng phương trình có hai nghiệm phân biệt với mọi m.

Câu 7: Tìm giá trị lớn nhất của biểu thức : A = 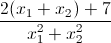$\frac{2(x_{1}+x_{2})+7}{x_{1}^{2}+x_{2}^{2}}$ .

Câu 8: Tìm các giá trị của m sao cho hai nghiệm của phương trình đều là số nguyên.

Cho hình vuông ABCD, điểm E thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc với DE, cắt DE ở H và cắt đường thẳng DC ở K.

Câu 9: Chứng minh rằng BHCD là tứ giác nội tiếp.

Câu 10: Tính số đo 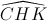$\widehat{CHK}$ .

Câu 11: Chứng minh hệ thức: KC.KD = KH.KB.

Câu 12: Khi điểm E di chuyển trên cạnh BC thì điểm H di chuyển trên đường nào?

Câu 13: Chứng minh rằng với a và b không âm, ta có : 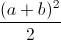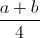$\frac{(a+b)^{2}}{2}$ + $\frac{a+b}{4}$ ≥ a√b + b√a.

Từ khóa » đề Số 23