Đề Thi Toán Lớp 5 Học Kì 1
Có thể bạn quan tâm
Mục Lục
- Đề 1 thi học kì 1 môn Toán lớp 5
- Đáp án đề thi học kì 1 môn Toán lớp 5
- Đề 2 thi học kì 1 môn Toán lớp 5
- Đáp án đề Toán 5 học kì 1
- Đề 3 thi học kì 1 môn Toán lớp 5
- Đề 4 thi Toán lớp 5 học kì 1
- Đáp án: Đề 4 kiểm tra học kì 1 Môn Toán lớp 5
- Đề 5 thi Toán lớp 5 học kì 1Phần I: Phần trắc nghiệm (6 điểm):
- Đáp án: Đề 5 kiểm tra học kì 1 Môn Toán lớp 5
- ĐỀ 6 THI HỌC KÌ 1 MÔN TOÁN LỚP 5
- Phần II. Tự luận (4 điểm)
- Đáp án & Thang điểm
- Đề số 7 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 8 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 9 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 10 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 11 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 12 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 13 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 14 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 9 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 10 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 11 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 12 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 13 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 14 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 15 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 16 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 17 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 18 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 19 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 20 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 21 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 22 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 23 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 24 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 25 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 26 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 27 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 28 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 29 – Đề kiểm tra học kì 1 – Toán lớp 5
- Đề số 30 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề 1 thi học kì 1 môn Toán lớp 5
| UBND THÀNH PHỐ……TRƯỜNG TH……….Họ và tên:Lớp 5……………………………. | KIỂM TRA ĐỊNH KÌ CUỐI HỌC KÌ INĂM HỌC: …Môn: TOÁN 5.Thời gian: 40 phút(Không kể thời gian giao đề) |
Chọn câu trả lời đúng nhất ở các câu 1, câu 3, câu 5, câu 6, câu 8 và thực hiện theo yêu cầu ở các câu 2, câu 4,câu 7, câu 9, câu 10.
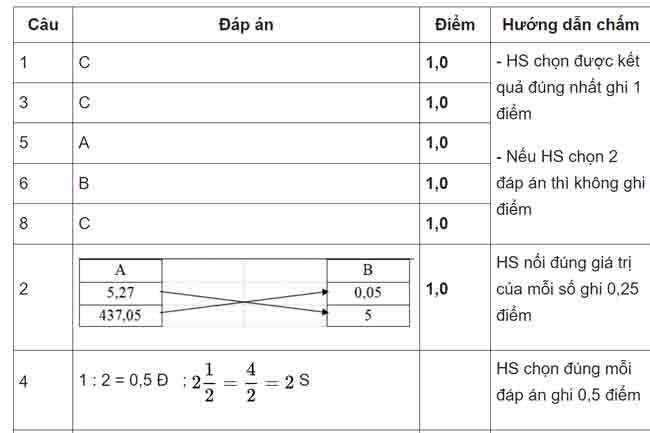
Câu 1: (1 điểm) (M1) Số thập phân “tám đơn vị, hai phần nghìn” được viết là:

Câu 3: (1 điểm) (M2) Số lớn nhất trong các số: 7,85 ; 6,58 ; 8,95 là:
A. 7,85B. 6.58C. 8,95
Câu 4: (1 điểm) (M1) Đúng ghi Đ, sai ghi S

Câu 5. (1 điểm) (M3) Một hình chữ nhật có chiều dài 2 m và chiều rộng 5 m thì diện tích hình chữ nhật trên là:
A. 10m2B. 10 mC. 100m2
Câu 6. ( 1điểm) (M1) Một con voi nặng 3tấn. Hỏi con voi đó nặng bao nhiêu ki-lô-gam?
A. 30kgB. 3000kgC. 30kg
Câu 7: (1 điểm) Đặt tính rồi tính. (M2)
a. 5,1 + 4,6b. 7,4 – 3,1c. 2,5 x 2d. 8,8 : 4
Câu 8: (1 điểm) (M3) Lớp 5A có 40 học sinh, trong đó số học sinh nữ là 30 em còn lại là học sinh nam. Tỉ số phần trăm của học sinh nữ và học sinh lớp 5A là:
A. 0,75B. 0,75%C. 75%
Câu 9: (1 điểm). (M3) Mua 3kg đường hết 45.000 đồng. Hỏi mua 5kg đường như thế hết bao nhiêu tiền?
Câu 10: (1điểm) (M4) Tính nhanh
16 x 40 + 16 x 460 + 16 x 500
Đáp án đề thi học kì 1 môn Toán lớp 5


Đề 2 thi học kì 1 môn Toán lớp 5
| Trường Tiểu học………………Họ và tên:…………………Lớp: 5A | BÀI KIỂM TRA ĐỊNH KÌ CUỐI HỌC KÌ IMôn : Toán – Lớp 5Năm học: …Thời gian làm bài: 40 phút |
Khoanh vào chữ cái trước câu trả lời đúng (Câu 1, 2, 3, 4, 8):
Câu 1 (1 điểm).
a, Hỗn số 2 34/1000 được viết dưới dạng số thập phân là:
A. 2,034B. 0,234C. 23,4D. 2,34
b, Chữ số 8 trong số 36,082 thuộc hàng nào?
A. Hàng đơn vịB. Hàng phần mườiC. Hàng phần trămD. Hàng phần nghìn
Câu 2 (1 điểm). Trong các số: 69,54; 9,07; 105,8; 28,3. Số bé nhất là:
A. 69,54B. 9,07C. 105,8D. 28,3
Câu 3 (1 điểm). Số thập phân thích hợp để viết vào chỗ chấm của 6hm2 47m2 = ……hm2 là:
A. 6,0047B. 6,047C. 6,47D. 0,647
Câu 4 (1 điểm). Tìm x, biết: x x 0,125 = 1,09. Vậy x là:
A. 0,872B. 87,2C. 8,72D. 872
Câu 5 (1 điểm). Đặt tính rồi tính:
a, 493,58 + 38,496 b, 970,5 – 184,68 c, 24,87 x 5,6 d, 364,8 : 3,04…………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………
Câu 6 (1 điểm). Đúng ghi Đ, sai ghi S vào ô trống:
a. Tỉ số phần trăm của hai số 10,26 và 36 là 2,85%. ☐
b. 65% của một số là 78. Vậy số đó là: 120. ☐
Câu 7 (1 điểm). Viết số thích hợp vào chỗ chấm để được câu trả lời đúng:
Mua 3kg đường cùng loại phải trả 54 000 đồng. Vậy mua 6,5kg đường như thế phải trả nhiều hơn ……………………… đồng.
Câu 8 (1 điểm). May một bộ quần áo hết 3,2m vải. Hỏi có 328,9m vải thì may được nhiều nhất bao nhiêu bộ quần áo như thế và còn thừa mấy mét vải?
A. 12 bộ quần áo, thừa 25m vải.B. 12 bộ quần áo, thừa 2,5m vải.C. 102 bộ quần áo, thừa 25m vải.D. 102 bộ quần áo, thừa 2,5m vải.
Câu 9 (1 điểm). Một mảnh đất hình chữ nhật có diện tích là 340,2m2 và chiều dài là 32,4m. Tính chu vi của mảnh đất đó.
…………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………
Câu 10 (1điểm). Hãy tìm hiểu lãi suất gửi ngân hàng ở địa phương em và tính xem nếu gửi 20 000 000 đồng thì sau một tháng cả số tiền gửi và tiền lãi là bao nhiêu?
…………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………
Đáp án đề Toán 5 học kì 1
Câu 1 (1 điểm). Mỗi ý đúng 0,5 điểm
a, Khoanh vào D.b, Khoanh vào C.
Câu 2 (1 điểm). Khoanh vào B.
Câu 3 (1 điểm). Khoanh vào A.
Câu 4 (1 điểm). Khoanh vào C.
Câu 5 (1điểm). Mỗi ý đúng 0,25 điểm
a, 493,58 + 38,496 = 532,076b, 970,5 – 184,68 = 785,82c, 24,87 x 5,6 = 139,272d, 364,8 : 3,04 = 120
Câu 6 (1 điểm). Mỗi ý đúng 0,5 điểm
a, S b, Đ
Câu 7 (1 điểm). 63 000.
Câu 8 (1 điểm). Khoanh vào D.
Câu 9 (1 điểm).
Bài giải
Chiều rộng mảnh đất đó là:
340,2 : 32,4 = 10,5 (m)
Chu vi mảnh đất đó là:
(32,4 + 10,5) x 2 = 85,8 (m)
Đáp số: 85,8 m.
Câu 10 (1 điểm). HS tự liên hệ thực tế rồi làm.
Chẳng hạn: Lãi suất gửi ngân hàng là 0,5% một tháng.
Số tiền lãi sau một tháng là:
20 000 000 : 100 x 0,5 = 100 000 (đồng)
Sau một tháng cả số tiền gửi và tiền lãi là:
20 000 000 + 100 000 = 20 100 000 (đồng)
Đáp số: 20 100 000 đồng.
Đề 3 thi học kì 1 môn Toán lớp 5
PHẦN I: TRẮC NGHIỆM: (3,5 điểm)
Khoanh vào chữ cái đặt trước câu trả lời hoặc đáp án đúng.
Câu 1. (0,5 điểm). Số thập phân có ba nghìn, một đơn vị, bảy phần trăm được viết là:
A. 3100,1
B. 3001,70
C. 3001,07
D. 3010,07
Câu 2. (0,5 điểm). Chữ số 5 trong số thập phân 127,056 có giá trị là:
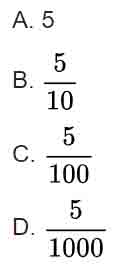
Câu 3. (0,5 điểm). Giá trị của biểu thức 70 + 8 + 0,6 + 0,005 là:
A. 78,65
B. 78,0605
C. 78,605
D. 78,6005
Câu 4. (0,5 điểm). Số thích hợp điền vào chỗ chấm 8,06 ha = ………. m2 là:
A. 86000
B. 80060
C. 80006
D. 80600

ta được:
A. 16%
B. 25%
C. 46%
D. 64%
Câu 6. (0,5 điểm). Mua 4 m vải phải trả 320 000 đồng. Hỏi mua 6,8 m vải cùng loại phải trả nhiều hơn bao nhiêu tiền?
A. 224 000 đồng
B. 544 000 đồng
C. 80 000 đồng
D. 2 176 000 đồng
Câu 7. (0,5 điểm). Bạn Việt mua 15 quyển vở giá 5000 đồng một quyển thì vừa hết số tiền đang có. Với số tiền đó nếu mua vở với giá 7500 đồng một quyển thì bạn Việt mua được bao nhiêu quyển vở?
A. 10 quyển
B. 20 quyển
C. 15 quyển
D. 30 quyển
PHẦN II: TỰ LUẬN: (6,5 điểm)
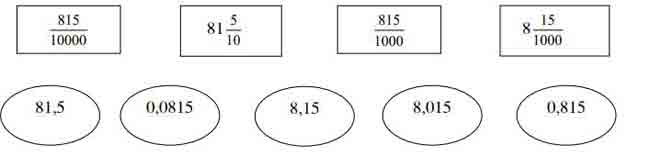
Câu 8. (1 điểm). Nối mỗi phân số (hỗn số) với số thập phân bằng nó.
Câu 9. (0,5 điểm). Điền số thích hợp vào chỗ trống.
Sau khi đi nhà sách mua đồ dùng học tập, em được cô bán hàng trả lại 50 000 đồng với đủ 3 loại giấy bạc 20 000 đồng, 10 000 đồng, 5 000 đồng. Vậy số tờ giấy bạc mỗi loại em có thể nhận được là:
a) ………….tờ 20 000 đồng, …………tờ 10 000 đồng, ………..tờ 5 000 đồng.
b) ………….tờ 20 000 đồng, …………tờ 10 000 đồng, ………..tờ 5 000 đồng.
Câu 10. (2 điểm). Đặt tính rồi tính.
a. 75,18 + 16,754
…………………
…………………
…………………
b. 345,1 – 17,25
…………………
…………………
…………………
c. 25,8 x 3,02
…………………….
…………………….
…………………….
d. 43,5 : 0,58
…………………….
…………………….
…………………….
Câu 11. (2 điểm). Một mảnh vườn hình chữ nhật có chiều rộng 45m và bằng 2/3 chiều dài.
a. Tính diện tích mảnh vườn?
b. Trên mảnh vườn đó, người ta trồng rau hết 80% diện tích. Tính diện tích đất còn lại chưa được sử dụng?
Câu 12. (1 điểm). Tính nhanh.
Câu 9. (0,5 điểm). Số tờ giấy bạc mỗi loại em có thể nhận được là:
a) 1 tờ 20000 đồng, 2 tờ 10000 đồng, 2 tờ 5000 đồng. (0,25 điểm)
b) 1 tờ 20000 đồng, 1 tờ 10000 đồng, 4 tờ 5000 đồng. (0,25 điểm)
Câu 10. (2 điểm) – Học sinh đặt tính, tính đúng mỗi phép tính được 0,5 điểm.
75,18 + 16,754 = 91,934
345,1 – 17,25 = 327,85
25,8 x 3,02 = 77,916
43,5 : 0,58 = 75
(Nếu đặt tính viết chưa thẳng cột trừ 0,25 điểm)
Câu 11. (2 điểm)
Chiều dài mảnh vườn là: 45 : 2/3 = 67,5 (m) (0,5 điểm)
Diện tích mảnh vườn là: 67,5 x 45= 3037,5 (m2) (0,5 điểm)
Diện tích trồng rau là 3037,5 x 80 :100 = 2430 (m2) (0,5 điểm)
Diện tích còn lại là: 3037,5 – 2430 = 607,5 (m2) (0,5 điểm)
Đáp số: 3037,5 m2; 607,5 m2
* Lưu ý: – Nếu HS làm theo cách khác mà đúng thì cũng được tính điểm tương đương. Khi
HS làm phép trừ tỉ số phần trăm mà không có ký hiệu tỉ số phần trăm (100% – 80% = 20%)
thì trừ một nửa số điểm của phép tính đó.
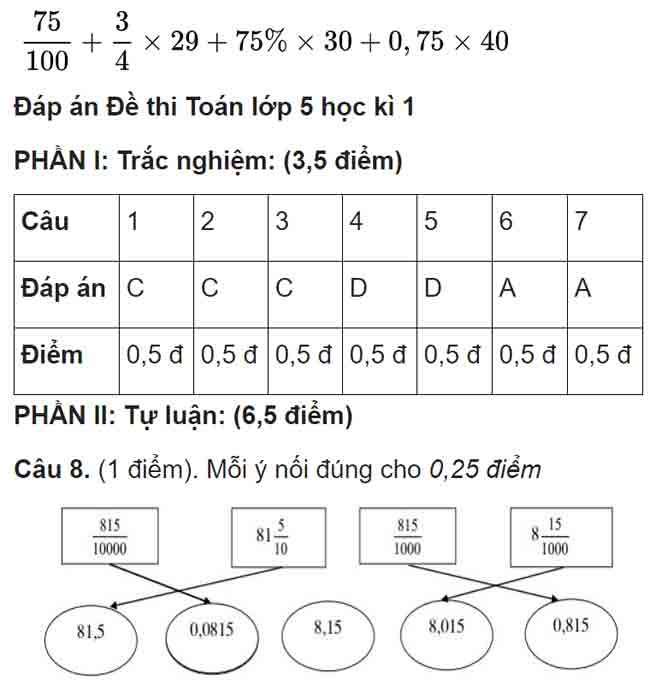
Câu 12 (1 điểm) Tính nhanh

= 0,75 x 1 + 0,75 x 29 + 0,75 x 30 + 0,75 x 40 (0,5 điểm)
= 0,75 x (1+ 29 + 30 + 40) (0,25 điểm)
= 0,75 x 100 = 75 (0,25 điểm)
Đề 4 thi Toán lớp 5 học kì 1
Bài 1 (1 điểm). a) Ghi lại cách đọc các số sau:
555,035:……………………………………………………………………………………….
:………………………………………………………………………………………………………………………….
b) Viết số thập phân gồm:
– Tám đơn vị, chín phần trăm:………………………………………………………………………………………….
– Hai nghìn không trăm mười tám đơn vị, bốn phần nghìn:………………………………………………….
Bài 2 (1 điểm). Điền dấu >, <, = vào chỗ chấm:
321,089…….321,1
534,1…….533,99
536,4…….536,400;
98,532…….98,45
Bài 3 (2 điểm). Đặt tính rồi tính
758,7 + 65,46
4,62 x 35,4
234,8 – 87
225,54 : 6,3
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
Bài 4 (1 điểm). Tìm X biết:
a) X – 13,1 = 7,53 x 6
b) 21 x X = 9,45 : 0,1
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
Bài 5 (1 điểm). Viết số thập phân thích hợp vào chỗ chấm:
8 km 62 m = …………km
2018 dm2 = ……………..m2
9 tấn 5 tạ = …………..tấn
5 giờ 15 phút = …………giờ
Bài 6 (2 điểm). Một mảnh vườn hình chữ nhật có nửa chu vi là 76m. Chiều rộng bằng 60% chiều dài.
a) Tính diện tích mảnh vườn đó.
b) Người ta sử dụng 8% diện tích mảnh vườn làm lối đi. Tìm diện tích lối đi.
Bài giải
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
……………………………………………………………………………………………………
………………………………………………………………………………………………….
…………………………………………………………………………………………………………………………………..
Bài 7 (1 điểm). Lãi suất tiết kiệm 1 tháng là 0,65%. Để sau 1 tháng nhận được tiền lãi là 780000 đồng thì khách hàng phải gửi bao nhiêu tiền?
Bài giải
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………….
Bài 8 (1 điểm). Khoanh vào chữ đặt trước câu trả lời đúng.
1) Giá trị của chữ số 6 ở phần thập phân trong số 63,546 là:
A. 6
B. 60
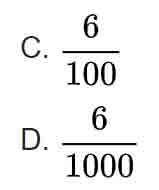

A. 75,8
B. 75,08
C. 75,008
D. 75,80
3) Trong các số 4,686; 4,688; 4,868; 4,288. Số bé nhất là:
A. 4,686
B. 4,688
C. 4,868
D. 4,288
4) 45% của 120 là:
A. 540
B. 54
C. 45
D. 12
Đáp án: Đề 4 kiểm tra học kì 1 Môn Toán lớp 5
Bài 1 (1 điểm). a)
555,035: Năm trăm năm mươi lăm phẩy không trăm ba mươi lăm

b) Viết số thập phân gồm:
– Tám đơn vị, chín phần trăm: 8,09
– Hai nghìn không trăm mười tám đơn vị, bốn phần nghìn: 2018,004
Bài 2 (1 điểm). Điền dấu >, <, = vào chỗ chấm:
321,089 < 321,1
534,1 > 533,99
536,4 = 536,400;
98,532 > 98,45
Bài 3 (2 điểm). Đặt tính rồi tính
KQ: 758,7 + 65,46 = 824,16
4,62 x 35,4 = 163,548
234,8 – 87 = 147,8
225,54 : 6,3 = 35,8
Bài 4 (1 điểm). Tìm X biết:
a) X – 13,1 = 7,53 x 6
X – 13,1 = 45,18
X = 45,18 + 13,1
X = 58,28
b) 21 x X = 9,45 : 0,1
21 x X = 94,5
X = 94,5 : 21
X = 4,5
Bài 5 (1 điểm). Viết số thập phân thích hợp vào chỗ chấm:
8 km 62 m = 8,062 km
2018 dm2 = 20,18 m2
9 tấn 5 tạ = 9,5 tấn
5 giờ 15 phút = 5,25 giờ
Bài 6 (2 điểm). Một mảnh vườn hình chữ nhật có nửa chu vi là 76 m. Chiều rộng bằng 60% chiều dài.
a) Tính diện tích mảnh vườn đó.
b) Người ta sử dụng 8% diện tích mảnh vườn làm lối đi. Tìm diện tích lối đi.
Bài giải
60% = 3/5
Sơ đồ:
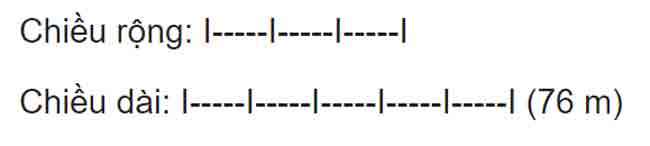
Chiều rộng mảnh vườn là:
76 : (3+5) x 3 = 28,5 (m)
Chiều dài mảnh vườn là:
76 – 28,5 = 47,5 (m)
Diện tích mảnh vườn:
28,5 x 47,5 = 1353,75 (m2)
Diện tích lối đi:
1353,75 : 100 x 8= 108,3 (m2)
Đáp số: Diện tích mảnh vườn 1353,75 (m2)
Diện tích lối đi 108,3 (m2)
Bài 7 (1 điểm). Lãi suất tiết kiệm 1 tháng là 0,65%. Để sau 1 tháng nhận được tiền lãi là 780000 đồng thì khách hàng phải gửi bao nhiêu tiền?
Bài giải
Số tiền khách hàng phải gửi là:
780000 : 0,65 x 100= 120000000 (đ)
Bài 8 (1 điểm). Khoanh vào chữ đặt trước câu trả lời đúng.
1) Giá trị của chữ số 6 ở phần thập phân trong số 63,546 là:

B. 75,08
3) Trong các số 4,686; 4,688; 4,868; 4,288. Số bé nhất là:
D. 4,288
4) 45% của 120 là:
B. 54
Đề 5 thi Toán lớp 5 học kì 1Phần I: Phần trắc nghiệm (6 điểm):
Câu 1: (M1 – 1 đ)
a) Số “Bốn mươi bảy đơn vị bốn phần mười và tám phần trăm” viết như sau:
A. 47,480
B. 47,48
C. 47,0480
D. 47,048
b) Phân số thập phân 834/10 được viết dưới dạng số thập phân là:
A. 0,0834
B. 0,834
C. 8,34
D. 83,4
Câu 2: (M1 – 1 đ)
a)- Chuyển đổi số thập phân 3, 03 thành hỗn số là:
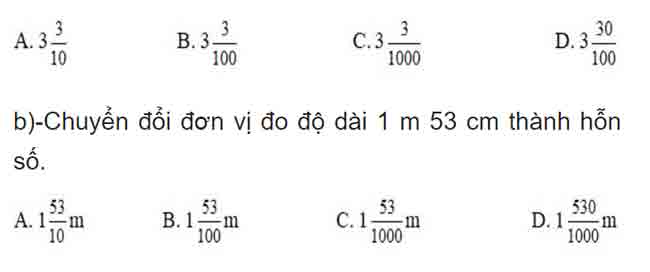
Câu 3: (M2 – 1 đ)
a)-Mua 2 quyển vở hết 24000 đồng. Vậy mua 10 quyển vở như thế hết số tiền là:
A. 60 000 đ
B. 600 000 đ
C. 240 000 đ
D. 120 000 đ
b) Lớp học có 25 học sinh, trong đó có 13 nữ. Số học sinh nữ chiếm bao nhiêu phần trăm của lớp học đó?
A. 13 %
B. 25%
C. 52 %
D. 25 %
Câu 4: (M2 – 1 đ)
A. 11
B. 12
C. 13
D. 14
b)-Tìm 15 % của 320 kg là
A. 320
B. 15
C. 48
D. 32
Câu 5: (M2 – 1 đ)
a) Vẽ chiều cao cho tam giác ABC sau. Biết cạnh đáy BC
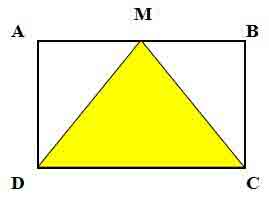
b) Cho hình chữ nhật ABCD có chiều dài 6 cm, chiều rộng 4 cm (như hình vẽ). Diện tích hình tam giác MDC bên trong hình chữ nhật là bao nhiêu?
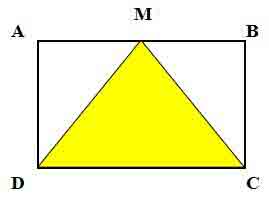
Diện tích hình tam giác MDC là:
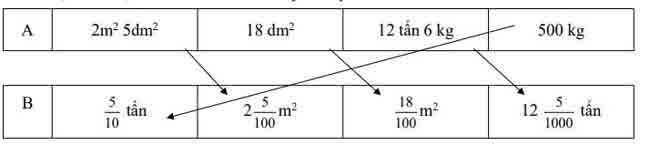
Câu 6: (M2 – 1 đ) Nối vế A với vế B cho phù hợp.

II.Tự Luận (4 điểm)
Câu 7: Tính biểu thức (M 3 – 1 đ)
a) (128,4 – 73,2): 2,4 – 18,32
b) 8,64: (1,46 + 3,34) + 6,32
Câu 8: Tìm x (M 3 – 1 đ)
25: x = 16: 10
210: x = 14,92 – 6,52
Câu 9: (M 3 – 1 đ)
Một hình chữ nhật ABCD có chiều dài 12, 15 m, chiều rộng bằng 2/5 chiều dài. Người ta cắt một phần đất AMD có dạng hình tam giác (như hình vẽ). Biết DM = 1/3 CD

Tính:
a) Diện tích phần đất đã cắt?
b) Diện tích đất còn lại?
Câu 10: (M 4 – 1 đ)
Cho một số có hai chữ số, khi ta viết thêm vào bên trái số đó một chữ số 1 thì tổng của số mới và số đã cho là 168. Tìm số đã cho.
Đáp án: Đề 5 kiểm tra học kì 1 Môn Toán lớp 5
Phần I: Phần trắc nghiệm (6 điểm):
Đường cao AH = h
Diện tích hình tam giác MDC là:
6 x 4 : 2 = 12 cm2
Câu 6: (M2 – 1 đ) Nối vế A với vế B cho phù hợp.
I.Tự Luận (4 điểm)
| Câu 7: Tính biểu thức (M 3 – 1 đ) |

Câu 9
Chiều rộng hình chữ nhật:

Diện tích hình tam giác ADM
4,86 x 8,1 : 2 = 19,638 (m2)
Diện tích đất còn lại:
59,049 – 19,683 = 39, 366 (m2)
Đáp số: a) 19,638 m2
b) 39, 366 m2
Câu 10: (M 4 – 1 đ)
Khi viết thêm 1 vào bên trái một số có hai chữ số,
ta được một số có ba chữ số, hơn số cũ 100 đơn vị.
Số đã cho là:
(168 – 100): 2 = 34
Đáp số: 34
ĐỀ 6 THI HỌC KÌ 1 MÔN TOÁN LỚP 5
Thời gian: 40 phút
Phần I. Trắc nghiệm (6 điểm)
Hãy khoanh tròn vào chữ cái đặt trước câu trả lời đúng:

Câu 4: (0,5 điểm) 3kg 5g = ……… kg Số thích hợp điền vào chỗ trống là:
A. 3,5 B. 3,50
C. 3,500 D. 3,005

Câu 6: (1 điểm) Tìm số tự nhiên x biết : 69,98 < x < 70,001
A. x = 69 B. x = 70
C. x = 69,99 D. x = 69,981
Câu 7: (1 điểm) Quan sát hình dưới đây và tính diện tích của hình thoi MNPQ. Biết: BC = 52 cm; AB = 75 cm

A. 3900 m2 B. 3900 cm2
C. 1950 cm D. 1950 cm2
Phần II. Tự luận (4 điểm)
Câu 1: (1 điểm) Tính :

a. Tính diện tích thửa ruộng đó.
b. Biết rằng, cứ 100m2 thu hoạch được 50kg thóc. Hỏi trên cả thửa ruộng đó người ta thu hoạch được bao nhiêu tạ thóc ?
Câu 3: (1 điểm) Tìm ba số thập phân thích hợp để viết vào chỗ chấm, sao cho: 0,2 < ……… < 0,23
Đáp án & Thang điểm
Phần I. Trắc nghiệm (6 điểm)
Học sinh khoanh đúng câu 1,4 mỗi câu 0,5 điểm các câu còn lại mỗi câu 1 điểm
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Đáp án | B | A | A | D | C | B | D |
Phần II. Tự luận (4 điểm)
Câu 1: (1điểm) – Tính đúng mỗi bài được (0,5đ)
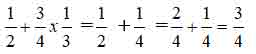
Câu 2: (2 điểm)
Chiều rộng thửa ruộng hình chữ nhật là: (0,5 đ)
60 : 3 x 2 = 40 (m)
Diện tích của thửa ruộng hình chữ nhật là ( 0,5 đ)
60 x 40 = 2400 (m2)
Trên cả thửa ruộng đó thu hoạch được số thóc là (0,5 đ)
2400 : 100 x 50 = 1200 (kg)
Đổi 1200kg = 12 tạ (0,25 đ) Đáp số : 12 tạ (0,25 đ)
Câu 3: (1 điểm)
Ba số thập phân thích hợp để viết vào chỗ chấm có thể là: 0,21; 0,22, 0,201
Câu 2, 3: Học sinh có cách làm khác phù hợp với đề bài, đúng được tính đủ điểm theo yêu cầu.
Đề số 7 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
I. PHẦN TRẮC NGHIỆM (3 điểm)
Khoanh vào chữ cái trước câu trả lời đúng
Câu 1. Số thập phân “tám đơn vị, hai phần nghìn” được viết là:
A. 82 B. 8,2
C. 8,02 D. 8,002

A. 0,0834 B. 0,834
C. 8,34 D. 83,4
Câu 3. Trong các số thập phân 42,538 ; 41,835 ; 42,358 ; 41,538 số thập phân lớn nhất là :
A. 42,538 B. 41,835
C. 42,358 D. 41,538
Câu 4. Mua 12 quyển vở hết 24000 đồng. Vậy mua 30 quyển vở như thế hết số tiền là :
A. 60000 đồng B. 72000 đồng
C. 6000 đồng D. 720 000 đồng
Câu 5. Một hình tam giác có độ dài đáy là 2m và chiều cao là 5,8dm thì diện tích hình tam giác trên là:
A. 116m2 B. 58dm2
C. 58m2 D. 116dm2
Câu 6.Chọn dấu thích hợp để điền vào chỗ chấm:
3,71 … 3,685
A. = B. > C. <
II. PHẦN TỰ LUẬN (7 điểm)
Bài 1. (2 điểm) Đặt tính rồi tính.
5,1 + 4,65 70,4 – 32,8
12,5 × 3 24 : 5
Bài 2. (2 điểm)Tìm xx, biết:
a) x × 4,8 = 60
b) 100 – x : 6 = 77,8
Bài 3. (2 điểm) Lớp 5A có 40 học sinh, trong đó số học sinh nữ là 30 em còn lại là học sinh nam. Tìm tỉ số phần trăm của học sinh nam và số học sinh lớp 5A.
Bài 4. (1 điểm) Tính nhanh
3,456 × 40 + 3,456 × 460 + 3,456 × 500
Lời giải
I. PHẦN TRẮC NGHIỆM
Câu 1.
Phương pháp:
– Dựa vào cấu tạo của số thập phân đã cho để viết số đó.
– Muốn viết một số thập phân, ta viết lần lượt từ hàng cao đến hàng thấp: trước hết viết phần nguyên, viết dấu “phấy”, sau đó viết phần thập phân.
Cách giải:
Số thập phân “tám đơn vị, hai phần nghìn” được viết là 8,002.
Chọn D.
Câu 2.
Phương pháp:

Chọn C.
Câu 3.
Phương pháp:
So sánh các số thập phân đã cho, từ đó tìm được số thập phân lớn nhất trong các số đó.
* Cách so sán hai số thập phân:
– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên của hai số đó bằng nhau,thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn … đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Cách giải:
So sánh các số đã cho ta có:
41,538 < 41,835 < 42,358 < 42,538.
Vậy số lớn nhất trong các số đã cho là 42,538.
Chọn A.
Câu 4.
Phương pháp:
Giải bài toán bằng phương pháp “rút về đơn vị”:
– Tìm số tiền khi mua 1 quyển vở ta lấy số tiền khi mua 12 quyển vở chia cho 12.
– Tìm số tiền khi mua 30 quyển vở ta lấy số tiền khi mua 1 quyển vở nhân với 30.
Cách giải:
Mua 1 quyển vở hết số tiền là:
24000 : 12 = 2000 (đồng)
Mua 30 quyển vở như thế hết số tiền là:
2000 × 30 = 60000 (đồng)
Đáp số: 60000 đồng.
Chọn C.
Câu 5.
Phương pháp:
– Đổi: 2m = 20dm.
– Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Cách giải:
Đổi: 2m = 20dm.
Diện tích hình tam giác đó là:
20 × 5,8 : 2 = 58 (dm2)
Đáp số: 58dm2.
Chọn B.
Câu 6.
Phương pháp:
Trong hai số nguyên có phần nguyên bằng nhau, số thập phân nào có hàng phần mười lớn hơn thì số đó lớn hơn.
Cách giải:
Ta có: 3,71 > 3,685 (vì phần nguyên bằng nhau, ở hàng phần mười có 7 > 6)
Chọn B.
II. PHẦN TỰ LUẬN
Bài 1.
Phương pháp:
Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia số thập phân.
Cách giải:
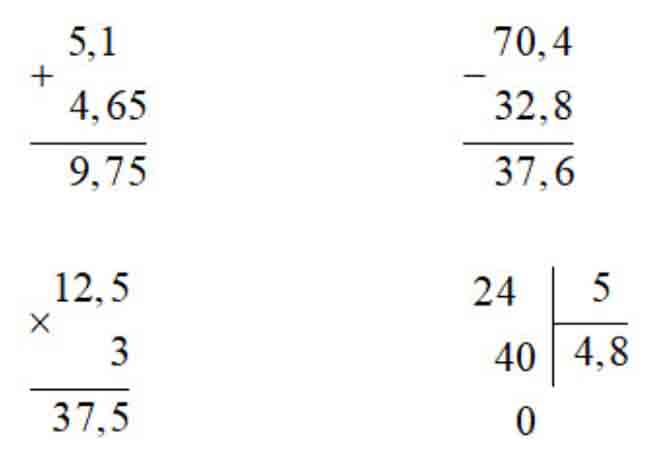
Bài 2.
Phương pháp:
Áp dụng các quy tắc:
– Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
– Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
– Muốn tìm số bị chia ta lấy thương nhân với số chia.
Cách giải:
a) x × 4,8 = 60
x = 60 : 4,8
x = 12,5
b) 100 – x : 6 = 77,8
x : 6 = 100 – 77,8
x : 6 = 22,2
x = 22,2 × 6
x = 133,2
Bài 3.
Phương pháp:
– Tìm số học sinh nam ta lấy số học sinh cả lớp trừ đi số học sinh nứ.
– Tìm tỉ số phần trăm của học sinh nam và số học sinh lớp 5A ta tìm thương của số học sinh nam và số học sinh lớp 5A, sau đó nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.
Cách giải:
Lớp 5A có số học sinh nam là:
40 – 30 = 10 (học sinh)
Tỉ số phần trăm của học sinh nam và số học sinh lớp 5A là:
10 : 40 = 0,25 = 25%
Đáp số: 25%.
Bài 4.
Phương pháp:
– Áp dụng công thức:
a × b + a × c + a × d = a × (b + c + d)
– Áp dụng cách nhân một số thập phân với 1000.
Cách giải:
3,456 × 40 + 16 × 460 + 16 × 500
= 3,456 × ( 40 + 460 + 500)
= 3,456 × 1000
= 3456
Đề số 8 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
I. PHẦN TRẮC NGHIỆM (3 điểm)
Khoanh vào chữ cái trước câu trả lời đúng

A. 2,034 B. 0,234
C. 23,4 D. 2,34
Câu 2. Chữ số 8 trong số 36,082 thuộc hàng nào?
A. Hàng đơn vị B. Hàng phần mười
C. Hàng phần trăm D. Hàng phần nghìn
Câu 3.Trong các số: 69,54; 9,07; 105,8; 28,3. Số bé nhất là:
A. 69,54 B. 9,07
C. 105,8 D. 28,3
Câu 4.Số thập phân thích hợp để viết vào chỗ chấm của 6hm2 47m2 = ……hm2 là:
A. 6,0047 B. 6,047
C. 6,47 D. 0,647
Câu 5. Tìm xx, biết: xx × 0,125 = 1,09. Vậy x là:
A. 0,872 B. 87,2
C. 8,72 D. 872
Câu 6. 10 người làm xong một sân trường phải hết một tuần lễ. Nay muốn làm xong sân trường đó trong 5 ngày thì cần bao nhiêu người? (sức làm của mỗi người như nhau)
A. 12 người B. 14 người
C. 15 người D. 20 người
II. PHẦN TỰ LUẬN (7 điểm)
Bài 1(2 điểm). Đặt tính rồi tính:
24,206 + 38,497
85,34 – 46,29
40,5 × 5,3
28,32 : 8
Bài 2 (1 điểm). Đúng ghi Đ, sai ghi S:
a) Tỉ số phần trăm của hai số 10,26 và 36 là 2,85%.
b) 65% của một số là 78. Vậy số đó là: 120.
Bài 3 (2,5 điểm). Một mảnh đất hình chữ nhật có diện tích là 340,2m2 và chiều dài là 32,4m. Tính chu vi của mảnh đất đó.
Bài 4(1,5 điểm). Hãy tìm hiểu lãi suất gửi ngân hàng ở địa phương em và tính xem nếu gửi 20 000 000 đồng thì sau một tháng cả số tiền gửi và tiền lãi là bao nhiêu?
Lời giải
I. PHẦN TRẮC NGHIỆM
Câu 1.
Phương pháp:

Chọn D.
Câu 2.
Phương pháp:
– Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
– Những chữ số thuộc phần nguyên theo thứ tự từ phải sang trái lần lượt thuộc hàng đơn vị, hàng chục, hàng trăm, hàng nghìn, …
– Những chữ số thuộc phần thập phân theo thứ tự từ trái sang phải lần lượt thuộc hàng phần mười, hàng phần trăm, hàng phần nghìn, …
Cách giải:
Chữ số 8 trong số 36,082 thuộc hàng phần trăm.
Chọn C.
Câu 3.
Phương pháp:
So sánh các số thập phân đã cho, từ đó tìm được số thập phân bé nhất trong các số đó.
* Cách so sán hai số thập phân:
– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên của hai số đó bằng nhau,thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn … đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Cách giải:
So sánh các số đã cho ta có:
9,07 < 28,3 < 69,54 < 105,8.
Vậy số bé nhất trong các số đã cho là 9,07.
Chọn B.
Câu 4.
Phương pháp:
– Xem lại cách viết các số đo diện tích dưới dạng số thập phân.
– Áp dụng cách chuyển đổi: 1hm2 = 10000m2 hay 1m2 =
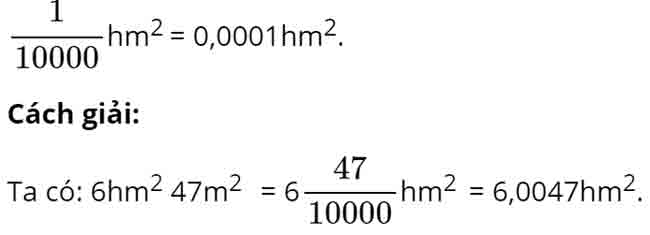
Vậy số thập phân thích hợp để viết vào chỗ chấm của 6hm2 47m2 = ……hm2 là 6,0047.
Chọn A.
Câu 5.
Phương pháp:
xx là thừa số chưa biết, muốn tìm xx ta lấy tích chia cho thừa số đã biết.
Cách giải:
xx × 0,125 = 1,09
xx = 1,09 : 0,125
xx = 8,72.
Chọn C.
Câu 6.
Phương pháp:
Giải bài toán bằng phương pháp “rút về đơn vị”:
– Tìm số người cần có nếu muốn làm xong sân trường trong 1 ngày.
– Tìm số người cần có nếu muốn làm xong sân trường trong 5 ngày.
Cách giải:
Đổi: 1 tuần lễ = 7 ngày
Muốn làm xong sân trường trong 1 ngày thì cần số người là:
10 × 7 = 70 (người)
Muốn làm xong sân trường đó trong 5 ngày thì cần số người là:
70 : 5 = 14 (người)
Đáp số: 14 người.
Chọn B.
II. PHẦN TỰ LUẬN
Bài 1.
Phương pháp:
Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia số thập phân.
Cách giải:

Bài 2.
Phương pháp:
a) Muốn tìm tỉ số phần trăm của hai số 10,26 và 36 ta tìm thương của 10,26 và 36, sau đó nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.
b) 65% của một số là 78. Muốn tìm số đó ta lấy 78 chia cho 65 rồi nhân với 100 hoặc lấy 78 nhân với 100 rồi chia cho 65.
Cách giải:
a) Tỉ số phần trăm của hai số 10,26 và 36 là:
10,26 : 36 = 0,285 = 28,5%
Vậy khẳng định “Tỉ số phần trăm của hai số 10,26 và 36 là 2,85% ” là sai.
⇒⇒ Điền S.
b) 65% của một số là 78. Vậy số đó là:
78 : 65 × 100 = 120.
Vậy khẳng định “65% của một số là 78. Vậy số đó là: 120.” là đúng.
⇒⇒ Điền Đ.
Bài 3.
Phương pháp:
– Tính chiều rộng = diện tích : chiều dài.
– Tính chu vi = (chiều dài + chiều rộng) × 2.
Cách giải:
Chiều rộng mảnh đất đó là:
340,2 : 32,4 = 10,5 (m)
Chu vi mảnh đất đó là:
(32,4 + 10,5) × 2 = 85,8 (m)
Đáp số: 85,8m.
Bài 4.
Phương pháp:
– Học sinh tự liên hệ thực tế để biết lãi suất gửi ngân hàng.
– Tìm số tiền lãi nhận được sau 1 tháng.
– Tìm tổng số tiền gốc và tiền lãi nhận được sau 1 tháng.
Cách giải:
Giả sử lãi suất gửi ngân hàng là 0,5% một tháng.
Số tiền lãi sau một tháng là:
20 000 000 : 100 × 0,5 = 100 000 (đồng)
Sau một tháng cả số tiền gửi và tiền lãi là:
20 000 000 + 100 000 = 20 100 000 (đồng)
Đáp số: 20 100 000 đồng.
Đề số 9 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
I. PHẦN TRẮC NGHIỆM
Khoanh vào chữ cái đặt trước câu trả lời đúng
Câu 1. Giá trị của chữ số 5 trong số thập phân 869,457 là:

Câu 2. Số thập phân mà phần nguyên là số lẻ nhỏ nhất có ba chữ số, phần thập phân là số chẵn lớn nhất có bốn chữ số là:
A. 101,9998 B. 111,1998
C. 103,1988 D. 100,8888
Câu 3: Điền dấu ( >, < hoặc = ) thích hợp vào chỗ trống
23ha 45m2 ……. 23,45ha
A. > B. = C. <
Câu 4.Tổng của hai số là 0,6. Thương của số bé và số lớn cũng bằng 0,6. Tìm hai số.
A.0,2 và 0,4 B. 0,225 và 0,375
C. 0,235 và 0,2 D. 0,48 và 0,12
Câu 5. Trong bể có 25 con cá, trong đó có 20 con cá chép. Tỉ số phần trăm của số cá chép và số cá trong bể là:
A. 5% B. 20%
C. 80% D. 100%
Câu 6. 45% của 120 là:
A. 540 B. 54
C. 45 D. 12
II. PHẦN TỰ LUẬN
Bài 1 (1 điểm): Đặt tính rồi tính:
146,34 + 521,85
745,5 – 14,92
25,04 × 3,5
66,15: 63
Bài 2 (2 điểm) Tính giá trị biểu thức:
a) 207,5 – 12,3 × 2,4 + 8,5
b) 502 – (45,5 + 22,5 × 12)
Bài 3 (3 điểm): Một mảnh đất hình chữ nhật có chiều dài 24m, chiều rộng kém chiều dài 4,5m.
a) Tính diện tích mảnh đất đó?
b) Người ta dành 15% diện tích đất để làm nhà. Tính diện tích phần đất làm nhà.
Bài 4 (1 điểm): Viết tiếp số thích hợp vào chỗ chấm
Lãi suất tiết kiệm là 0,6% một tháng. Một người gửi tiết kiệm 10 000 000 đồng. Sau 1 tháng cả số tiền gửi và số tiền lãi là: ………………….. đồng.
Lời giải
I. PHẦN TRẮC NGHIỆM
Câu 1.
Phương pháp:
Xác định hàng của chữ số 5 trong số thập phân đã cho, từ đó xác định giá trị của chữ số đó.
Cách giải:
Chữ số 5 trong số thập phân 879,457 thuộc hàng phần trăm nên có giá trị là
5/100
Chọn D.
Câu 2.
Phương pháp:
– Tìm số lẻ nhỏ nhất có ba chữ số và số chẵn lớn nhất có bốn chữ số.
– Muốn viết một số thập phân, ta viết lần lượt từ hàng cao đến hàng thấp: trước hết viết phần nguyên, viết dấu “phấy”, sau đó viết phần thập phân.
Cách giải:
Số lẻ nhỏ nhất có ba chữ số là 101.
Số chẵn lớn nhất có bốn chữ số là 9998.
Vậy số thập phân cần tìm là 101,9998.
Chọn A.
Câu 3.
Phương pháp:
Viết các số đo về cùng đơn vị đo là ha rồi so sánh kết quả với nhau.
Cách giải:

– Tìm số bé và số lớn theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Cách giải:

Coi số bé gồm 3 phần bằng nhau thì số lớn gồm 5 phần như thế.
Tổng số phần bằng nhau là:
3 + 5 = 8 (phần)
Số bé là:
0,6 : 8 × 3 = 0,225
Số lớn là:
0,6 – 0,225 = 0,375
Đáp số: Số bé: 0,225 ;
Số lớn: 0,375.
Chọn B.
Câu 5.
Phương pháp:
Muốn tìm tỉ số phần trăm của số cá chép và số cá trong bể ta tìm thương của số cá chép và số cá trong bể, sau đó nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.
Cách giải:
Tỉ số phần trăm của số cá chép và số cá trong bể là:
20 : 25 = 0,8 = 80%
Đáp số: 80%.
Chọn C.
Câu 6.
Phương pháp:
Muốn
Cách giải:
45% của 120 là :
120 : 100 × 45 = 54
Hoặc: 120 × 45 : 100 = 54
Chọn B.
II. PHẦN TỰ LUẬN
Bài 1.
Phương pháp:
Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia số thập phân.
Cách giải:
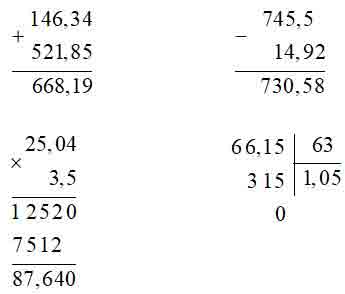
Bài 2.
Phương pháp:
– Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
– Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.
Cách giải:
a) 207,5 – 12,3 × 2,4 + 8,5
= 207,5 – 29,52 + 8,5
= 177,98 + 8,5
= 186,48
b) 502 – (45,5 + 22,5 × 12)
= 502 – (45,5 + 270)
= 502 – 315,5
= 186,5
Bài 3.
Phương pháp:
– Tính chiều rộng ta lấy chiều dài trừ đi 4,5m.
– Tính diện tích ta lấy chiều dài nhân với chiều rộng.
– Tính diện tích phần đất làm nhà ta lấy diện tích mảnh đất chia cho 100 rồi nhân với 15 hoặc lấy diện tích mảnh đất nhân với 15 rồi chia cho 100.
Cách giải:
a) Chiều rộng mảnh đất hình chữ nhật là:
24 – 4,5 = 19,5 (m)
Diện tích mảnh đất hình chữ nhật là:
24 × 19,5 = 468 (m2)
b) Diện tích phần đất làm nhà là:
468 : 100 × 15 = 70,2 (m2)
Đáp số: a) 468m2;
b) 70,2m2.
Bài 4.
Phương pháp:
– Tính số tiền lãi ta lấy số tiền gửi chia cho 100 rồi nhân với 0,6.
– Tính tổng số tiền gửi và tiền lãi = tiền gửi + tiền lãi.
Cách giải:
Số tiền lãi sau một tháng là:
10 000 000 : 100 × 0,6 = 60 000 (đồng)
Sau một tháng cả số tiền gửi và tiền lãi là:
10 000 000 + 60 000 = 10 060 000 (đồng)
Đáp số: 10 060 000 đồng.
Đề số 10 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
I. PHẦN TRẮC NGHIỆM (3 điểm)
Khoanh tròn vào chữ cái (A,B,C,D) trước câu trả lời đúng nhất
Câu 1. Số “ Tám mươi chín phẩy bảy mươi bảy” viết là:
A. 809,77 B. 89,77
C. 89,707 D. 98,77
Câu 2. Số lớn nhất trong các số 5,25; 5,52; 5,7; 5,58 là:
A. 5,52 B. 5,25
C. 5,7 D. 5,58
Câu 3. Số 0,55 viết dưới dạng tỉ số phần trăm là:
A. 0,55% B. 5,5%
C. 55% D. 550%
Câu 4. Giá trị của biểu thức 8,6 × (5,7 – 4,7 ) + 5,6 : 4 là:
A. 10 B. 12
C. 7,5 D. 3,55
Câu 5. 6dm2 15cm2 = … dm2 . Số thích hợp điền vào chỗ chấm là:
A. 615 B. 61,5
C. 6,0015 D. 6,15
Câu 6. Một hình tam giác có độ dài đáy là 4,5cm, chiều cao 2,4cm. Tính điện tích hình tam giác đó.
A. 10,8cm2 B. 5,4cm2
C. 21,6cm2 D. 4,8cm2
II. PHẦN TỰ LUẬN
Bài 1. (2 điểm) Đặt tính rồi tính:
12,47 + 39,68
657,21 – 198,34
109,8 × 5,4
91,08 : 3,6
Bài 2. (2 điểm) Tìm xx:
a) 9,8 : xx = 2,8 + 7
b) xx + 25,6 = 86,5 : 2,5
Bài 3. (2 điểm) Một trại chăn nuôi có số gà và vịt là 1575 con, trong đó 40% là vịt, còn lại là gà. Hỏi trại chăn nuôi đó có bao nhiêu con gà, bao nhiêu con vịt ?
Bài 4. (1 điểm) Tính bằng cách thuận tiện nhất:
a) 16,9 + 8,4 + 3,1 + 1,6
b) 34,5 × 6,7 + 34,5 × 3,3
Lời giải
I. PHẦN TRẮC NGHIỆM
Câu 1.
Phương pháp:
Muốn viết một số thập phân, ta viết lần lượt từ hàng cao đến hàng thấp: trước hết viết phần nguyên, viết dấu “phấy”, sau đó viết phần thập phân.
Cách giải:
Số “ Tám mươi chín phẩy bảy mươi bảy” viết là 89,77.
Chọn B.
Câu 2.
Phương pháp:
So sánh các số thập phân đã cho, từ đó tìm được số thập phân bé nhất trong các số đó.
* Cách so sán hai số thập phân:
– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên của hai số đó bằng nhau,thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn … đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Cách giải:
So sánh các số đã cho ta có:
5,25 < 5,52 < 5,58 < 5,7.
Vậy số lớn nhất trong các số đã cho là 5,7.
Chọn C.
Câu 3.
Phương pháp:
Muốn viết số 0,55 dưới dạng tỉ số phần trăm ta nhân 0,55 với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.
Cách giải:
Ta có: 0,55 = 55%.
Chọn C.
Câu 4.
Phương pháp:
– Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
– Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.
Cách giải:
8,6 × (5,7 – 4,7 ) + 5,6 : 4
= 8,6 × 1 + 1,4
= 8,6 + 1,4
= 10
Chọn A.
Câu 5.
Phương pháp:
– Xem lại cách viết các số đo diện tích dưới dạng số thập phân.
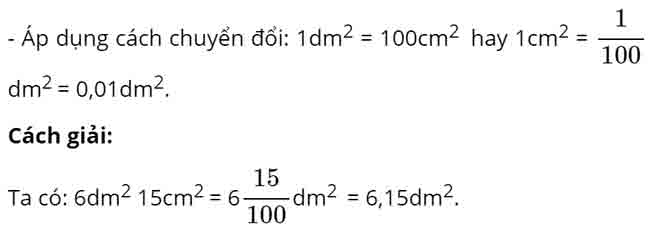
Vậy số thập phân thích hợp để viết vào chỗ chấm của 6dm2 15cm2 = … dm2là 6,15.
Chọn D.
Câu 6.
Phương pháp:
Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Cách giải:
Diện tích hình tam giác đó là:
4,5 × 2,4 : 2 = 5,4 (cm2)
Đáp số: 5,4cm2.
Chọn B.
II. PHẦN TỰ LUẬN
Bài 1.
Phương pháp:
Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia số thập phân.
Cách giải:

Bài 2.
Phương pháp:
– Tính giá trị vế phải trước.
– Áp dụng các quy tắc:
+ Muốn tìm số chia ta lấy số bị chia chia cho thương.
+ Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
Cách giải:
a) 9,8 : xx = 2,8 + 7
9,8 : xx = 9,8
xx = 9,8 : 9,8
xx = 1
b) xx + 25,6 = 86,5 : 2,5
xx + 25,6 = 34,6
xx = 34,6 – 25,6
xx = 9
Bài 3.
Phương pháp:
– Tìm số con gà ta lấy tổng số con gà và vịt (1575 con) chia cho 100 rồi nhân với 40 hoặc lấy tổng số con gà và vịt (1575 con) nhân với 40 rồi chia cho 100.
– Tìm số con vịt ta lấy tổng số con gà và vịt trừ đi số con gà.
Cách giải:
Trại chăn nuôi đó có số con gà là:
1575 : 100 × 40 = 630 (con)
Trại chăn nuôi đó có số con vịt là:
1575 – 630 = 945 (con)
Đáp số: Gà: 630 con ;
Vịt: 945 con.
Bài 4.
Phương pháp:
a) Áp dụng tính chất giao hoán và kết hợp để ghép 16,9 và 3,1 thành một nhóm, ghép 8,4 và 1,6 thành một nhóm.
b) Áp dụng công thức: a × b + a × c = a × (b + c).
Cách giải:
a) 16,9 + 8,4 + 3,1 + 1,6
= (16,9 + 3,1) + (8,4 + 1,6)
= 20 + 10
= 30
b) 34,5 × 6,7 + 34,5 × 3,3
= 34,5 × (6,7 + 3,3)
= 34,5 × 10
= 345
Đề số 11 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Khoanh vào chữ cái trước câu trả lời đúng :
Câu 1. Số “Bốn mươi bảy đơn vị, bốn phần mười và tám phần trăm ” viết như sau:
A. 47,48 B. 47,408
C. 47,0480 D. 47,048
Câu 2. Viết số thập phân thích hợp vào chỗ chấm:
3m 8cm = … m
A. 38 B. 3,8
C. 3,08 D. 3,008
Câu 3. Tìm một số biết 25% của nó là 438. Số đó là :
A. 1652 B. 1752
C. 1852 D. 1952
Câu 4. Phân số 1/2 được viết dưới dạng tỉ số phần trăm là:
A. 0,5% B. 1,2%
C. 12% D. 50%
Câu 5: Lớp học có 25 học sinh, trong đó có 13 nữ. Hỏi số học sinh nữ chiếm bao nhiêu phần trăm của lớp học đó?
A. 13% B. 25%
C. 52% D. 48%
Câu 6: Một bồn hoa hình tam giác có diện tích là 18m2 , độ dài đáy là 7,5m. Chiều cao của bồn hoa đó là:
A. 6m B. 4,8m
C. 2,4m D. 13,5m
II. PHẦN TỰ LUẬN : (7 điểm)
Bài 1. Đặt tính rồi tính (2 điểm)
926,83 + 549,7
987,054 – 456,18
12,6 × 7,3
9,6 : 1,25
Bài 2. Tìm xx (2 điểm)
a) 2,4 : \(x\) = 16 : 10
b) \(x\) × 3,5 = 104,92 – 47,52
Bài 3. Một mảnh đất hình chữ nhật có chiều dài 48m, chiều rộng bằng 1212 chiều dài. Người ta dành 25% diện tích mảnh đất để đào ao. Tính diện tích đất đào ao.(2 điểm)
Bài 4. Tìm một số thập phân biết nếu dịch chuyển dấu phẩy của số đó sang trái 1 chữ số thì được số mới mà tổng của số mới và số cần tìm là 19,25. (1 điểm)
Lời giải
I. PHẦN TRẮC NGHIỆM
Câu 1.
Phương pháp:
– Dựa vào cấu tạo của số thập phân đã cho để viết số đó.
– Muốn viết một số thập phân, ta viết lần lượt từ hàng cao đến hàng thấp: trước hết viết phần nguyên, viết dấu “phấy”, sau đó viết phần thập phân.
Cách giải:
Số “Bốn mươi bảy đơn vị, bốn phần mười và tám phần trăm ” viết là 47,48.
Chọn A.
Câu 2.
Phương pháp:
– Xem lại cách viết các số đo độ dài dưới dạng số thập phân.

Chọn C.
Câu 3.
Phương pháp:
25% của một số là 438. Muốn tìm số đó ta lấy 438 chia cho 25 rồi nhân với 100 hoặc lấy 438 nhân với 100 rồi chia cho 25.
Cách giải:
Số cần tìm là:
438 : 25 × 100 = 1752
Chọn B.
Câu 4.
Phương pháp:


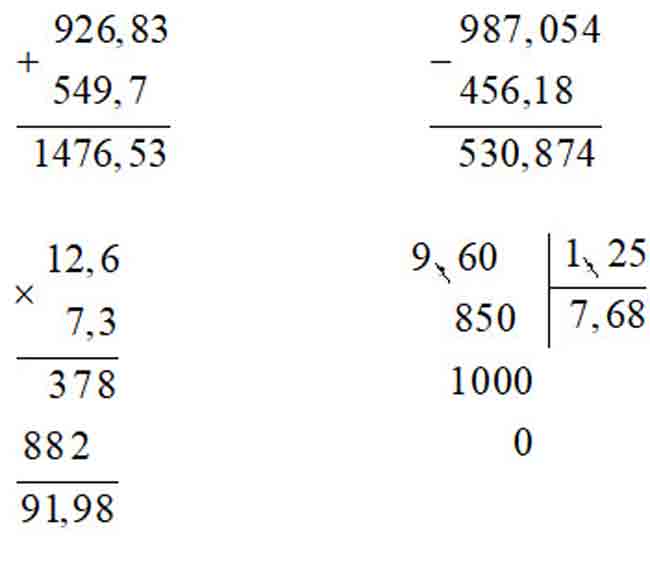
Bài 2.
Phương pháp:
– Tính giá trị vế phải trước.
– Áp dụng các quy tắc:
+ Muốn tìm số chia ta lấy số bị chia chia cho thương.
+ Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
Cách giải:
a) 2,4 : xx = 16 : 10
2,4 : xx = 1,6
xx = 1,5
b) xx × 3,5 = 104,92 – 47,52
xx × 3,5 = 57,4
xx = 57,4 : 3,5
xx = 16,4
Bài 3.
Phương pháp:

Diện tích mảnh đất là :
48 × 24 = 1152 (m2)
Diện tích phần đất đào ao là :
1152 : 100 × 25 = 288 (m2)
Đáp số: 288m2.
Bài 4.
Phương pháp:
Nếu chuyển dịch dấu phẩy của số phải tìm sang bên trái một chữ số ta được số mới giảm đi 10 lần.

Tìm số phải tìm theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Cách giải:
Nếu chuyển dịch dấu phẩy của số phải tìm sang bên trái một chữ số ta được số mới giảm đi 10 lần.
Coi số mới gồm 1 phần thì số phải tìm gồm 10 phần như thế.
Tổng số phần bằng nhau là:
10 + 1 = 11 (phần)
Số phải tìm là:
19,25 : 11 × 10 = 17,5
Đáp số: 17,5.
Đề số 12 – Đề kiểm tra học kì 1 – Toán lớp 5
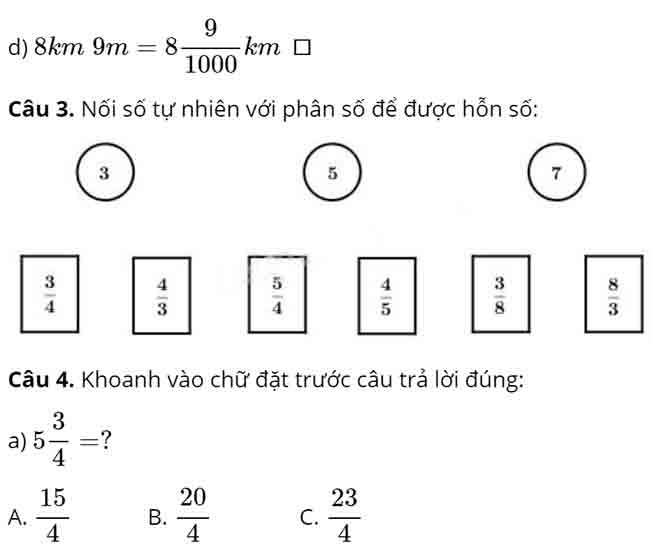
Đề bài
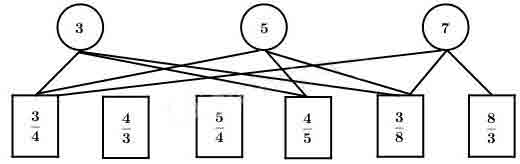
Câu 1. Khoanh vào chữ số đặt trước câu trả lời đúng:


Câu 7. Có hai vòi nước cùng chảy vào một bẻ không chứa nước. Nếu vòi thứ nhất chaỷ riêng thì sau 9h sẽ đầy bể. Nếu vòi thứ hai chảy riêng thì sau 6 giờ sẽ đầy bể.
Hỏi hai vòi cùng chảy lúc 8 giờ 24 phút thì đến mấy giờ đầy nước?
Câu 8. Tìm a biết a là số tự nhiên:
Lời giải
Câu 1.
Phương pháp:
Chuyển hỗn số thành phân số rồi so sánh hai phân số như thông thường.
Cách giải:
Chọn C.
Câu 2.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo độ dài:

Vậy ta có đáp án như sau:
a) S; b) Đ;
c) S; d) Đ.
Câu 3.
Phương pháp:
Dựa vào tính chất: Phần phân số của hỗn số bao giờ cũng bé hơn đơn vị.
Cách giải:
Câu 4.
Phương pháp:
*) Có thể viết hỗn số thành một phân số có:
– Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.
– Mẫu số bằng mẫu số ở phần phân số.
*) Để viết phân số dưới dạng hỗn số ta lấy tử số chia cho mẫu số, thương trong phép chia chính là phần nguyên, phần phân số có tử số là số dư còn mẫu số là mẫu số của phân số ban đầu.
Cách giải:

Chọn B.
Câu 5.
Phương pháp:
– Đổi hai số đo về cùng đơn vị đo rồi so sánh kết quả với nhau.
– Áp dụng cách đổi: 11 tấn =10=10 tạ.
Cách giải:
Ta có:
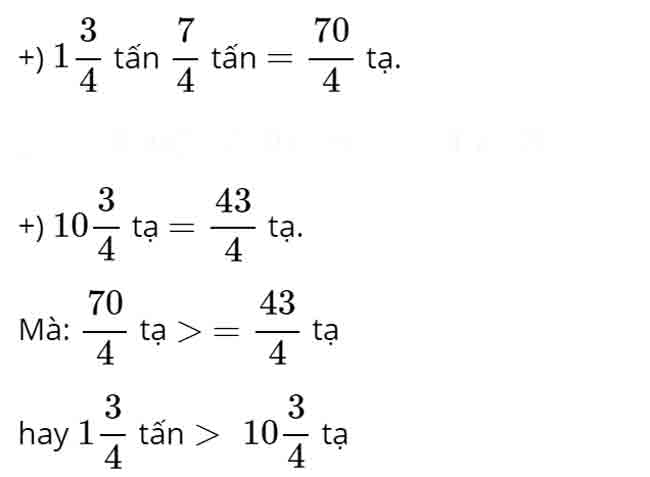
Vậy ta có đáp án như sau:
a) S; b) S; c) Đ.
Câu 6.
Phương pháp:
Đổi hỗn số thành phân số rồi thực hiện phép tính với các phân số như thông thường.
Cách giải:
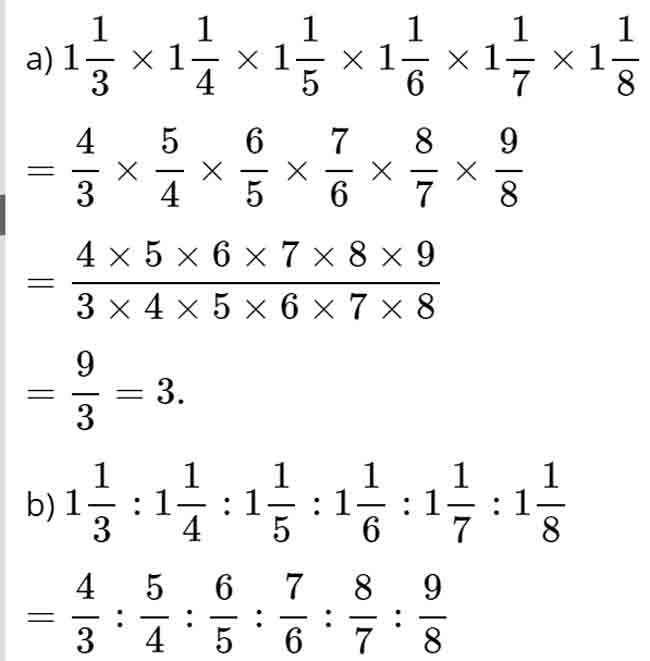
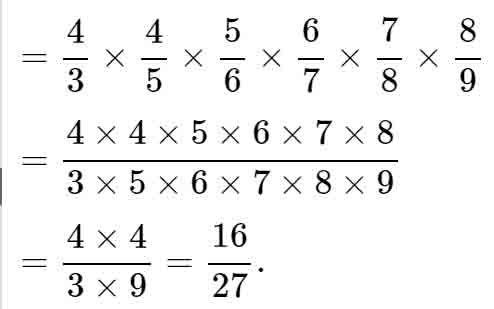
Câu 7.
Phương pháp:
– Coi cả bể nước là 11 đơn vị.
– Tìm số phần bể nước vòi thứ nhất hoặc vòi thứ hai chảy được trong 11 giờ ta lấy 11 chia cho số giờ để vòi thứ nhất hoặc vòi thứ hai chảy đầy bể.
– Tính tổng số phần bể nước vòi thứ nhất và vòi thứ hai chảy được trong 11 giờ.
– Tìm số giờ để bể đầy nước nếu hai vòi cùng chảy ta lấy 11 chia cho tổng số phần bể nước vòi thứ nhất và vòi thứ hai chảy được trong 11 giờ.
– Tìm thời gian lúc bể đầy nước ta lấy thời gian lúc hai vòi bắt đầu chảy vào bể cộng với thời gian hai vòi chảy đầy bể
Cách giải:
Trong 1 giờ vòi thứ nhất chảy được số phần bể nước là:

Bể đầy nước lúc:
88 giờ 2424 phút +3+3 giờ 3636 phút =12=12 giờ
Đáp số: 1212 giờ .
Câu 8.
Phương pháp:
– Tính giá trị ở vế trái rồi từ đó tìm số tự nhiên thích hợp.
– Biểu thức có dấu ngoặc thì ta tính trong ngoặc trước, ngoài ngoặc sau.
Cách giải:
Ta có:
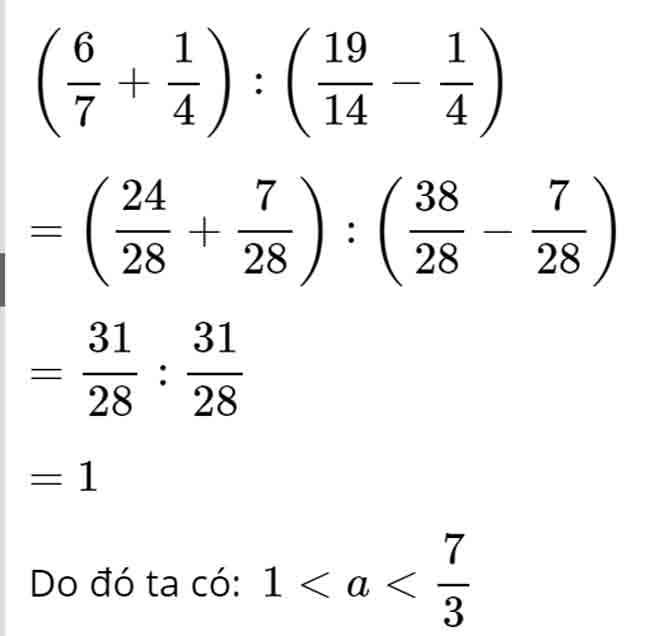
Vì aa là số tự nhiên nên a=2.
Đề số 13 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:
Tổng của hai số là 376376. Số thứ hai bằng 3535 số thứ nhất. Tìm hai số đó.
a) Số thứ nhất là 141
Số thứ hai là 235
b) Số thứ nhất là 235
Số thứ hai là 141
Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:

A. 330 và 570
B. 336 và 576
C. 348 và 588
Câu 3. Đúng ghi Đ, sai ghi S:
Một ô tô đi trong 5 giờ được 225km. Hỏi ô tô đó đi trong 8 giờ được bao nhiêu ki-lô-mét?
a) 320km ☐
b) 345km ☐
c) 360km ☐
Câu 4. Đúng ghi Đ, sai ghi S:
Một tổ công nhân có 4 người làm xong một công việc trong 12 ngày. Nếu chỉ có 3 người thì làm xong công việc đó trong mấy ngày? (năng suất làm của mọi người như nhau và không thay đổi).
a) 200 ngày ☐
b) 18 ngày ☐
c) 16 ngày ☐
Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:
Một mảnh vườn hình chữ nhật có chu vi là 120m, chiều rộng bằng 2323chiều dài. Tính diện tích mảnh vườn đó.
A. 800m2 ☐
B. 864 m2 ☐
C. 3456 m2 ☐
Câu 6. Mẹ cho hai anh em 40 cái kẹo. Số kẹo của em gấp rưỡi số kẹo của anh. Hỏi mẹ cho mỗi người bao nhiêu cái kẹo?
Câu 7. Dùng một số tiền để mua gạo tẻ với giá 6000 đồng/1kg thì mua được 30kg. Với số tiền đó mua gạo nếp với giá 900 đồng/1kg thì được bao nhiêu ki-lô-gam?
Câu 8. Mua 5m vải hết 120 000 đồng. Hỏi mua 15m vải như thế hết bao nhiêu tiền?
Lời giải
Câu 1.
Phương pháp:
Tìm hai số theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Cách giải:
Ta có sơ đồ:

Theo sơ đồ, tổng số phần bằng nhau là:
3+5=83+5=8 (phần)
Số thứ nhất là:
376:8×5=235376:8×5=235
Số thứ hai là:
376−235=141376−235=141
Đáp số: Số thứ nhất: 235235;
Số thứ hai: 141141.
Vậy ta có kết quả như sau:
a) S; b) Đ
Câu 2.
Phương pháp:
Tìm hai số theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
Cách giải:

nhau thì số lớn gồm 1212 phần như thế.
Hiệu số phần bằng nhau là:
12−7=512−7=5 (phần)
Số bé là:
240:5×7=336240:5×7=336
Số lớn là:
336+240=576336+240=576
Đáp số: Số bé: 336336;
Số lớn: 576576.
Chọn B.
Câu 3.
Phương pháp:
Có thể giải bằng phương pháp rút về đơn vị:
– Tìm số ki-lô-mét ô tô đi được trong 11 giờ ta lấy số ki-lô-mét ô tô đi được trong 55 giờ chia cho 55.
– Tìm số ki-lô-mét ô tô đi được trong 88 giờ ta lấy số ki-lô-mét ô tô đi được trong 11 giờ nhân với 88.
Cách giải:
Trong 11 giờ ô tô đi được số ki-lô-mét là:
225:5=45(km)225:5=45(km)
Trong 11 giờ ô tô đi được số ki-lô-mét là:
45×8=360(km)45×8=360(km)
Đáp số: 360km360km.
Vậy ta có kết quả như sau:
a) S; b) S; c) Đ.
Câu 4.
Phương pháp:
Càng có ít người thì số ngày hoàn thành công việc càng nhiều. Đây là bài toán về quan hệ tỉ lệ.
Để giải bài toán về quan hệ tỉ lệ, ta có thể dùng phương pháp “rút về đơn vị” hoặc phương pháp “tìm tỉ số”.
Cách giải:
11 người làm xong công việc đó trong số ngày là:
12×4=4812×4=48 (ngày)
Nếu chỉ có 3 người thì làm xong công việc đó trong số ngày là:
48:3=1648:3=16 (ngày)
Đáp số: 1616 ngày.
Vậy ta có kết quả như sau: a) S; b) S; c) Đ.
Câu 5.
Phương pháp:
– Tính nửa chu vi == chu vi :2:2.
– Tìm chiều dài, chiều rộng theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.
– Tính diện tích == chiều dài ×× chiều rộng.
Cách giải:
Nửa chu vi mảnh vườn đó là:
120:2=60;(m)120:2=60;(m)
Ta có sơ đồ:
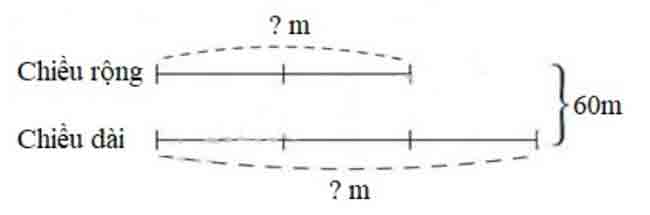
Theo sơ đồ, tổng số phần bằng nhau là:
2+3=52+3=5 (phần)
Chiều rộng mảnh vườn đó là:
60:5×2=24(m)60:5×2=24(m)
Chiều dài mảnh vườn đó là:
60−24=36(m)60−24=36(m)
Diện tích mảnh vườn đó là:
36×24=864(m2)36×24=864(m2)
Đáp số: 864m2.864m2.
Chọn B.
Câu 6.
Phương pháp:
– Số kẹo của em gấp rưỡi số kẹo của anh tức là số kẹo của em
bằng 3/2 số kẹo của em.
– Tìm số kẹo của mỗi người theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Cách giải:
Số kẹo của em gấp rưỡi số kẹo của anh tức là số kẹo của em bằng 3/2 số kẹo của em.
Ta có sơ đồ:
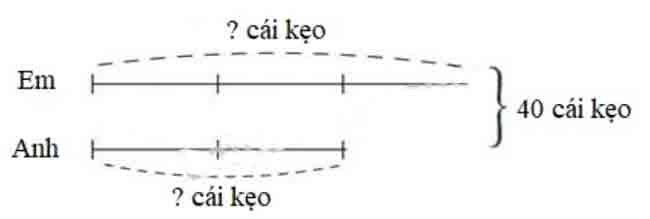
Theo sơ đồ, tổng số phần bằng nhau là:
3+2=53+2=5 (phần)
Số kẹo của em là:
40:5×3=2440:5×3=24(cái)
Số kẹo của anh là :
40−24=1640−24=16(cái)
Đáp số: Em: 2424 cái ;
Anh: 1616 cái.
Câu 7.
Phương pháp:
– Tìm tổng số tiền ta lấy giá tiền mua 1kg1kg gạo tẻ nhân với số ki-lô-gam gạo tẻ.
– Tìm số ki-lô-gam gạo nếp mua được ta lấy tổng số tiền chia cho giá tiền mua 1kg1kg gạo nếp.
Cách giải:
Có tổng số tiền là:
6000×30=1800006000×30=180000 (đồng)
Mua được số ki-lô-gam gạo nếp là:
180000:9000=20(kg)180000:9000=20(kg)
Đáp số: 20kg20kg.
Câu 8.
Phương pháp:
Càng mua nhiều vải thì số tiền càng nhiều. Đây là bài toán về quan hệ tỉ lệ.
Để giải bài toán về quan hệ tỉ lệ, ta có thể dùng phương pháp “rút về đơn vị” hoặc phương pháp “tìm tỉ số”.
Cách giải:
Cách 1 (Rút về đơn vị):
Mua 1m1m vải hết số tiền là:
120000:5=24000120000:5=24000 (đồng)
Mua 15m15m vải hết số tiền là:
24000×15=36000024000×15=360000 (đồng)
Đáp số: 360000360000 đồng.
Cách 2 (Tìm tỉ số):
15m15m vải gấp 5m5m vải số lần là:
15:5=315:5=3 (lần)
Mua 15m15m vải hết số tiền là:
120000×3=360000120000×3=360000 (đồng)
Đáp số: 360000360000 đồng.
Đề số 14 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:
Tổng của hai số là số lớn nhất có hai chữ số. Tìm hai số đó biết nếu viết thêm một chữ số 0 vào bên phải số bé thì được số lớn.
A. 10 và 90
B. 9 và 99
C. 9 và 90.
Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:
Một mảnh đất hình chữ nhật có chiều rộng bằng 2525 chiều dài. Nếu chiều rộng tăng thêm 9m, chiều dài bớt đi 9m thì mảnh đất trở thành hình vuông.
Tính diện tích mảnh đất đó.
A. 300m2 B. 360m2 C. 420m2
Câu 3. Đúng ghi Đ, sai ghi S:
Một người đi xe máy trong 16 phút được 9km 600m. Hỏi với
mức đi như thế trong

giờ thì người đó đi được bao nhiêu ki-lô-mét?
giờ thì người đó đi được bao nhiêu ki-lô-mét?
a) 108km b) 150km c) 192km
Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng:
18 người làm xong một đoạn đường mất 5 ngày. Hỏi 30 người làm xong đoạn đường đó trong bao nhiêu ngày? (Biết sức làm việc của mỗi người là như nhau).
A. 2 ngày B. 3 ngày C. 4 ngày
Câu 5. Tổng số tuổi hiện nay của hai mẹ con là 36 tuổi. Tuổi con bằng

tuổi mẹ. Hỏi:
a) Hiện nay mỗi người bao nhiêu tuổi?
b) Mấy năm sau tuổi mẹ gấp 3 lần tuổi con?
Câu 6. 6 người thợ trong 4 giờ quét vôi trên tường được 120m2. Hỏi 8 người thợ quét vôi trong mấy giờ thì được 200m2. Biết năng suất làm việc của mỗi người như nhau.
Lời giải
Câu 1.
Phương pháp:
– Tìm tổng của hai số: số lớn nhất có hai chữ số là 9999.
– Viết thêm một chữ số 00 vào bên phải số bé thì được số lớn nên số lớn gấp 1010 lần số bé.
– Tìm hai số theo dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Cách giải:
Số lớn nhất có hai chữ số là 9999 nên tổng của hai số là 9999.
Viết thêm một chữ số 00 vào bên phải số bé thì được số lớn nên số lớn gấp 1010 lần số bé, tức là nếu coi số bé gồm 11 phần thì số lớn gồm 1010 phần như thế.
Tổng số phần bằng nhau là:
1+10=111+10=11 (phần)
Số bé là:
99:11=999:11=9
Số lớn là:
99−9=9099−9=90
Đáp số: Số bé: 99;
Số lớn: 9090.
Chọn C.
Câu 2.
Phương pháp:
– Tìm hiệu giữa chiều dài và chiều rộng: nếu chiều rộng tăng thêm 9m, chiều dài bớt đi 9m thì mảnh đất trở thành hình vuông nên hiệu giữa chiều dài và chiều rộng là: 9+9=18m9+9=18m.
– Tìm chiều dài và chiều rộng theo bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
– Tìm diện tích == chiều dài ×× chiều rộng.
Cách giải:
Nếu chiều rộng tăng thêm 9m, chiều dài bớt đi 9m thì mảnh đất trở thành hình vuông nên hiệu giữa chiều dài và chiều rộng là:
9+9=18(m)9+9=18(m)
Ta có sơ đồ:

Theo sơ đồ, hiệu số phần bằng nhau là:
5−2=35−2=3 (phần)
Chiều rộng mảnh đất đó là:
18:3×2=12(m)18:3×2=12(m)
Chiều dài mảnh đất đó là:
12+18=30(m)12+18=30(m)
Diện tich mảnh đất đó là:
30×12=360(m2)30×12=360(m2)
Đáp số: 360m2.360m2.
Chọn B.
Câu 3.
Phương pháp:


a) S; b) S; c) Đ.
Câu 4.
Phương pháp:
Càng có nhiều người thì số ngày làm xong đoạn đường đó càng ít. Đây là bài toán về quan hệ tỉ lệ.
Để giải bài toán về quan hệ tỉ lệ, ta có thể dùng phương pháp “rút về đơn vị” hoặc phương pháp “tìm tỉ số”.
Cách giải:
(Phương pháp rút về đơn vị)
11 người làm xong đoạn đường đó trong số ngày là:
5×18=905×18=90 (ngày)
30 người làm xong đoạn đường đó trong số ngày là:
90:30=390:30=3 (ngày)
Đáp số: 33 ngày.
Chọn B.
Câu 5.
Phương pháp:
– Tìm tuổi của mỗi người theo dạng toán tìm hai số khi biết tổng và tỉ số.
– Dựa vào nhận xét: Mỗi năm mỗi người tăng 1 tuổi nên hiệu số tuổi hai mẹ con không thay đổi.
Cách giải:
a) Ta có sơ đồ:
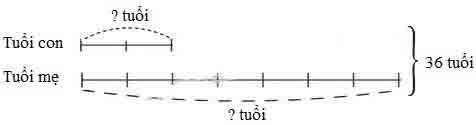
Theo sơ đồ, tổng số phần bằng nhau là:
2+7=92+7=9 (phần)
Tuổi mẹ hiện nay là:
4×7=284×7=28 (tuổi)
Tuổi con hiện nay là:
4×2=84×2=8 (tuổi)
b) Mẹ hơn con số tuổi là:
28−8=2028−8=20 (tuổi)
Mỗi năm mỗi người tăng 11 tuổi nên hiệu số tuổi hai mẹ con không thay đổi. Vậy khi tuổi mẹ gấp 3 lần tuổi con, mẹ vẫn hơn con 20 tuổi.
Coi tuổi con khi đó gồm 11 phần thì tuổi mẹ khi đó gồm 33 phần như thế.
Hiệu số phần bằng nhau là:
3−1=23−1=2 (phần)
Tuổi con khi đó là:
20:2×1=1020:2×1=10 (tuổi)
Số năm sau để tuổi mẹ gấp 3 lần tuổi con là:
10−8=210−8=2 (năm)
Đáp số: a) Mẹ: 2828 tuổi ; con: 88 tuổi.
b) 22 năm.
Câu 6.
Phương pháp:
– Tính số mét vuông tường 66 người thợ quét được trong 11 giờ ta lấy số mét vuông tưởng 66 người thợ quét được trong 44 giờ chia cho 44.
– Tính số mét vuông tường 11 người thợ quét được trong 11 giờ ta lấy số mét vuông tưởng 66 người thợ quét được trong 11 giờ chia cho 66.
– Tính số mét vuông tường 88 người thợ quét được trong 11 giờ ta lấy số mét vuông tưởng 11 người thợ quét được trong 11 giờ nhân với 88.
– Tính số giờ để 88 người thợ quét được 200m2200m2 ta lấy 200200 chia cho số mét vuông tường 88 người thợ quét được trong 11 giờ.
Cách giải:
Trong 11 giờ, 66 người thợ quét được số mét vuông tường là:
120:4=30(m2)120:4=30(m2)
Trong 11 giờ, 11 người thợ quét được số mét vuông tường là:
30:6=5(m2)30:6=5(m2)
Trong 11 giờ, 88 người quét được số mét vuông tường là:
5×8=40(m2)5×8=40(m2)
Vậy 88 người thợ quét 200m2200m2 hết số giờ là:
200:40=5200:40=5 (giờ)
Đáp số: 55 giờ.
Đề số 9 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Khoanh vào chữ đạt trước câu trả lời đúng:
Điền số thích hợp vào chỗ chấm:
350m = ……… cm.
A. 3500
B. 35 000
C. 350 000
Câu 2. Điền dấu (>,=,<)(>,=,<) vào chỗ chấm:

Câu 3. Đúng ghi Đ, sai ghi S:
Điền số thích hợp vào chỗ chấm:
50000kg=50000kg= ……. tấn
a) 5000 ☐ b) 500 ☐
c) 50 ☐ d) 5 ☐
Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng:
Một cửa hàng bán ngày thứ nhất được 4 tạ 5kg gạo. Ngày thứ

Hỏi cả hai ngày bán được bao nhiêu ki-lô-gam gạo?
A. 540kg B. 620kg C. 648kg
Câu 5. Đúng ghi Đ, sai ghi S:
a) Tính: 4km 7m + 124m – 2km 95m = ?
2km 36m ☐
2km 540m ☐
2km 450m ☐
b) Tính: 13kg 25g – 7kg 30g + 495g = ?
6kg 49g ☐
6kg 490g ☐
6kg 940g ☐
Câu 6. Xe tải thứ nhất trở được 3 tấn 260kg rau xanh. Xe tải thứ hai chở được ít hơn xe tải thứ nhất 120kg nhưng lại nhiều hơn xe tải thứ ba 540kg. Hỏi trung bình mỗi xe chở được mấy tấn rau xanh?
Câu 7. Ba đội công nhân phải sửa một đoạn đường dài 8km

sửa. Hỏi mỗi đội sửa được bao nhiêu mét đường?
Lời giải
Câu 1:
Phương pháp:
Dựa vào cách đổi: 1m=100cm1m=100cm
Cách giải:
Ta có 1m=100cm1m=100cm nên 350m=35000cm350m=35000cm.
Chọn B.
Câu 2.
Phương pháp:
Đổi các số đo về cùng một đơn vị đo rồi so sánh kết quả với nhau.
Cách giải:

b) 2km5m=2km+5m=2000m+5m=2005m
Vậy: 2km5m=2005m
c) 4hm3m=4hm+3m=400m+3m=403m
Mà: 430m>403m430m>403m
Vậy: 430m>4hm3m
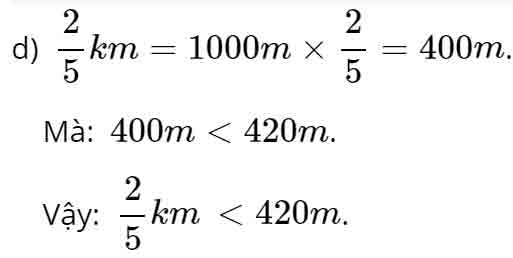
Câu 3.
Phương pháp:
Dựa vào cách đổi: 11 tấn =1000kg=1000kg.
Cách giải:
Ta có: 11 tấn =1000kg=1000kg.
Nhẩm: 50000:1000=5050000:1000=50.
Vậy: 50000kg=5050000kg=50 tấn.
Ta có kết quả như sau:
a) S; b) S;
c) Đ; d) S.
Câu 4.
Phương pháp:
– Đổi 44 tạ 5kg=405kg5kg=405kg.
– Tính số gạo bán ngày thứ hai ta lấy số gạo bán ngày thứ

Cả hai ngày cửa hàng bán được số ki-lô-gam gạo là:
405+243=648(kg)405+243=648(kg)
Đáp số: 648kg.648kg.
Chọn C.
Câu 5.
Phương pháp:
– Đổi các số đo về cùng một đơn vị đo rồi thực hiện tính giá trị biểu thức như thông thường.
Lưu ý rằng: 1km=1000m;1kg=1000g1km=1000m;1kg=1000g.
– Biểu thức chỉ có phép cộng và phép trừ thì ta tính lần lượt từ trái sang phải.
Cách giải:
a) 4km7m+124m–2km95m4km7m+124m–2km95m
=4007m+124m−2095m=4007m+124m−2095m
=4131m−2095m=4131m−2095m
=2036m=2km36m=2036m=2km36m
Vậy kết quả là: Đ; S; S.
b) 13kg25g–7kg30g+495g13kg25g–7kg30g+495g
=13025g−7030g+495g=13025g−7030g+495g
=5995g+495g=5995g+495g
=6490g=6kg490g=6490g=6kg490g
Vậy kết quả là: S; Đ; S.
Câu 6.
Phương pháp:
– Đổi 33 tấn 260kg=3260kg260kg=3260kg.
– Tìm số rau xe thứ hai chở được ta lấy số rau xe thứ nhất chở được trừ đi 120kg120kg.
– Tìm số rau xe thứ ba chở được ta lấy số rau xe thứ hai chở được cộng với 540kg540kg.
– Tìm số rau trung bình mỗi xe chở được ta lấy tổng số rau ba xe chở được chia cho 3.
– Đổi số đo vừa tìm được sang đơn vị tấn, lưu ý ta có 11 tấn =1000kg=1000kg.
Cách giải:
Đổi: 33 tấn 260kg=3260kg260kg=3260kg.
Xe tải thứ nhất chở được số ki-lô-gam rau là:
3260–120=3140(kg)3260–120=3140(kg)
Xe tải thứ hai chở được số ki-lô-gam rau là:
3140–540=2600(kg)3140–540=2600(kg)
Cả ba xe chở được số ki-lô-gam rau là:
3260+3140+2600=9000(kg)3260+3140+2600=9000(kg)
Trung bình mỗi xe chở được số ki-lô-gam rau là:
9000:3=3000(kg)9000:3=3000(kg)
3000kg=33000kg=3 tấn
Đáp số: 33 tấn.
Câu 7.
Phương pháp:
– Đổi 8km460m=8460m8km460m=8460m.
– Tính số mét đường đội một sửa được ta lấy độ dài đoạn


Đề số 10 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:
Điền dấu (>,=,<)(>,=,<)vào chỗ chấm:
a) 20km 5m ……… 20050m
20km 5m > 20050m ☐
20km 5m = 20050m ☐
20km 5m < 20050m ☐
b) 3kg 15g ……… 3015g
3kg 15g > 3015g ☐
3kg 15g = 3015g ☐
3kg 15g < 3015g ☐
Câu 2. Đúng ghi Đ, sai ghi S:

con lợn. Hỏi cả hai con nặng bao nhiêu ki-lô-gam?
A.72kg B. 96kg C. 120kg
Câu 4. Bao nhiêu thứ nhất có nhiều hơn bao thứ hai 40kg gạo. Sau khi mỗi bao bán đi 20kg gạo thì số gạo còn lại ở bao

Lời giải
Câu 1.
Phương pháp:
Đổi các số đo về cùng một đơn vị đo rồi so sánh kết quả với nhau.
Lưu ý cách chuyển đổi: 1km=1000m1km=1000m ; 1kg=1000g1kg=1000g.
Cách giải:
a) 20km5m=20km+5m20km5m=20km+5m=20000m+5m=20005m=20000m+5m=20005m.
Mà 20005m<20050m20005m<20050m
Vậy: 20km5m<20050m20km5m<20050m.
Ta có kết quả là: S; S; Đ.
b) 3kg;15g=3kg+15g3kg;15g=3kg+15g =3000g+15g=3015g=3000g+15g=3015g.
Mà: 3015g=3015g3015g=3015g
Vậy: 3kg;15g=3015g3kg;15g=3015g.
Ta có kết quả là: S; Đ; S.
Câu 2.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:

Vậy ta có kết quả như sau:
a) S ; b) Đ ;
c) S ; d) Đ.
Câu 3.
Phương pháp:


Theo sơ đồ, hiệu số phần bằng nhau là:
5−3=25−3=2 (phần)
Con dê cân nặng số ki-lô-gam là:
24:2×3=36(kg)24:2×3=36(kg)
Con lợn cân nặng số ki-lô-gam là:
36+24=60(kg)36+24=60(kg)
Cả hai con cân nặng số ki-lô-gam là:
36+60=96(kg)36+60=96(kg)
Đáp số: 96kg.96kg.
Chọn B.
Câu 4.
Phương pháp:
– Nếu mỗi bao bán đi 20kg20kg gạo thì hiệu số gạo hai bao không thay đổi và bằng 40kg40kg.
– Ta tìm số gạo còn lại của mỗi bao theo dạng toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
– Tìm số gạo lúc đầu đầu của mỗi bao ta lấy số gạo còn lại cộng với số gạo đã bán đi.
Cách giải:
Nếu mỗi bao bán đi 20kg20kg gạo thì hiệu số gạo hai bao không thay đổi và bằng 40kg40kg.
Ta có sơ đồ:
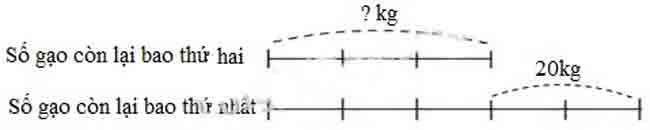
Theo sơ đồ, hiệu số phần bằng nhau là:
5−3=25−3=2 (phần)
Sau khi bán đi 20kg20kg, bao thứ hai còn lại số gạo là:
40:2×3=60(kg)40:2×3=60(kg)
Lúc đầu bao thứ hai có số ki-lô-gam gạo là:
60+20=80(kg)60+20=80(kg)
Lúc đầu bao thứ nhất có số ki-lô-gam gạo là:
80+40=120(kg)80+40=120(kg)
Đáp số: Bao thứ nhất: 120kg120kg;
Bao thứ hai: 80kg80kg.
Câu 5.
Phương pháp:

số đo ba cạnh của bồn hoa hay chu vi bồn hoa.
– Tìm số đo cạnh thứ nhất ta lấy chu vi bồn hoa trừ đi tổng số đo cạnh thứ hai và cạnh thứ ba.
– Tìm số đo cạnh thứ hai ta có thể lấy chu vi bồn hoa trừ đi tổng số đo cạnh thứ nhất và cạnh thứ ba.
– Tìm số đo cạnh thứ ba ta có thể lấy tổng số đo cạnh thứ hai và cạnh thứ ba trừ đi số đo cạnh thứ hai.
Cách giải:
22 lần tổng số đo ba cạnh của bồn hoa hay 22 lần chu vi bồn hoa là:


Đề số 11 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:
a) 20dam2=200m220dam2=200m2 ☐
b) 20dam2=2000m220dam2=2000m2 ☐
c) 12000m2=120km212000m2=120km2 ☐
d) 12000m2=12km212000m2=12km2 ☐
Câu 2. Đúng ghi Đ, sai ghi S:
a) 300hm2=30000dam2300hm2=30000dam2 ☐
b) 300hm2=3000dam2300hm2=3000dam2 ☐
c) 125000dam2=125hm2125000dam2=125hm2 ☐
d) 125000dam2=1250hm2125000dam2=1250hm2 ☐
Câu 3. Đúng ghi Đ, sai ghi S:
a) 15000mm2=1500cm215000mm2=1500cm2 ☐
b) 15000mm2=150cm215000mm2=150cm2 ☐
c) 42000cm2=420dm242000cm2=420dm2 ☐
d) 42000cm2=4200dm242000cm2=4200dm2 ☐
Câu 4. Đúng ghi Đ, sai ghi S:

Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:
Một khu đất hình chữ nhật có chiều dài 200m. Chiều rộng

Hỏi thừa ruộng đó có diện tích bao nhiêu đề-ca-mét vuông?
Câu 8. Một căn phòng hình chữ nhật có chiều rộng 6m, chiều dài gấp rưỡi chiều rộng. Người ra lát nền căn phòng đó bằng loại gạch vuông cạnh 3dm.
Hỏi căn phòng đó lát hết bao nhiêu viên gạch (diện tích phần mạch vữa không đáng kể).
Lời giải
Câu 1.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:
1dam2=100m21dam2=100m2 ; 1km2=1000000m21km2=1000000m2
Cách giải:
+) 1dam2=100m21dam2=100m2 nên 20dam2=2000m220dam2=2000m2;
+) 1km2=1000000m21km2=1000000m2 nên 12km2=12000000m212km2=12000000m2 ; 120km2=120000000m2120km2=120000000m2
Ta có kết quả như sau:
a) S; b) Đ; c) S; d) S.
Câu 2.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:
1hm2=100dam21hm2=100dam2 ; 1km2=1000000m21km2=1000000m2
Cách giải:
+) 1hm2=100dam21hm2=100dam2 nên 300hm2=30000dam2300hm2=30000dam2.
+) Tính nhẩm: 125000:100=1250125000:100=1250, do đó ta có: 125000dam2=1250hm2125000dam2=1250hm2.
Ta có kết quả như sau:
a) Đ; b) S; c) S; d) Đ.
Câu 3.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo: 1cm2=10000mm21cm2=10000mm2 ; 1dm2=100cm21dm2=100cm2 .
Cách giải:
+) Ta có: 1cm2=100mm21cm2=100mm2.
Tính nhẩm: 15000:100=15015000:100=150
Do đó: 15000mm2=150cm215000mm2=150cm2.
+) 1dm2=100cm21dm2=100cm2
Tính nhẩm: 42000:100=42042000:100=420.
Do đó: 42000cm2=420dm242000cm2=420dm2.
Ta có kết quả như sau:
a) S; b) Đ; c) Đ; d) S.
Câu 4.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:

Ta có kết quả như sau:
a) S; b) Đ; c) S;
d) Đ; e) S; g) Đ.
Câu 5.
Phương pháp:

Diện tích khu đất là :
200×150=30000(m2)200×150=30000(m2)
30000m2=3ha30000m2=3ha
Đáp số: 3ha3ha.
Chọn D.
Câu 6.
Phương pháp:
Ta có 1ha=10000m21ha=10000m2 nên để đổi số đo từ đơn vị haha sang đơn vị m2m2 ta lấy 10000 nhân với số đó.
Cách giải:
Ta có 1ha=10000m21ha=10000m2 nên

– Tính diện tích thửa ruộng = độ dài đáy ×× chiều cao.
– Đổi số đo diện tích sang đơn vị đo là đề-ca-mét vuông, lưu ý rằng 1dam2=100m21dam2=100m2.
Cách giải:
Đổi: 5dam4m=54m
Chiều cao thửa ruộng đó là:

– Tính diện tích căn phòng = chiều dài ×× chiều rộng; sau đó đổi sang đơn vị đo là đề-xi-mét vuông.
– Tính diện tích một viên gạch vuông = cạnh ×× cạnh.
– Tính số gạch cần dùng = diện tích căn phòng :: diện tích một viên gạch vuông.
Cách giải:

Diện tích căn phòng đó là:
9×6=54(m2)9×6=54(m2)
54m2=5400dm254m2=5400dm2
Diện tích viên gạch để lát nền là:
3×3=9(dm2)3×3=9(dm2)
Số gạch dùng để lát căn phòng đó là :
5400:9=6005400:9=600(viên)
Đáp số: 600600 viên.
Đề số 12 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:

Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:
Điền hỗn số vào chỗ chấm:

Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:

đo hai đường chéo. Hỏi chu vi hình thoi đó là bao nhiêu xăng-ti-mét?
Câu 7. Một khu đất hình chữ nhật có chiều dài hơn chiều rộng 35m. Nếu mỗi chiều tăng thêm 5m thì diện tích tăng thêm là 1450m2. Hỏi khu đất đó có diện tích là bao nhiêu héc-ta?
Lời giải
Câu 1.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:

Ta có kết quả như sau:
a) S; b) Đ; c) Đ;
d) S; e) S; g) Đ.
Câu 2.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:
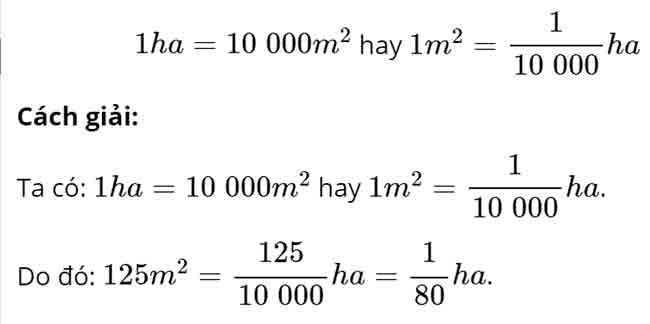
Ta có kết quả như sau: a) S; b) Đ; c) S.
Câu 3.
Phương pháp:
Áp dụng cách chuyển đổi các đơn vị đo:

Chọn C.
Câu 4.
Phương pháp:
– Đổi các số đo về cùng đơn vị đo rồi so sánh kết quả với nhau.

– Tính diện tích còn lại = diện tích khu an dưỡng −− diện tích hồ nước.
Cách giải:

Chọn D.
Câu 6.
Phương pháp:


Đáp số: 32cm
Câu 7.
Phương pháp:
– Vẽ hình dựa vào dữ kiện đề bài (xem hình trong phần lời giải).
– Chia phần tăng thêm thành các hình chữ nhật nhỏ, dựa vào diện tích và độ dài cạnh đã biết để tính độ dài còn lại.
– Áp dụng các công thức:
Diện tích = chiều dài ×× chiều rộng;
Chiều dài = diện tích : chiều rộng ;
Chiều rộng = diện tích : chiều dài.
Cách giải:
Theo đề bài ta có hình vẽ:
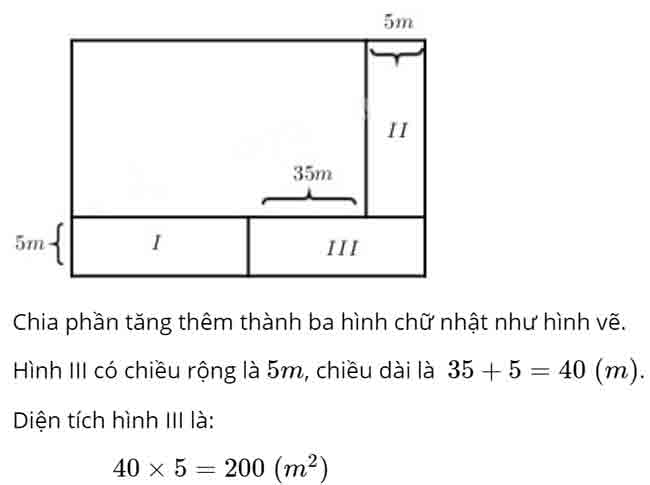
Hình I bằng hình II vì đều có chiều rộng bằng 5m5m và chiều dài bằng chiều rộng cũ của khu đất.
Tổng diện tích khu đất hình I và hình II là:
1450−200=1250(m2)
Diện tích hình I hay hình II là :
1250:2=625(m2)1250:2=625(m2)
Chiều rộng của khu đất là :
625:5=125(m)625:5=125(m)
Chiều dài của khu đất là :
125+35=160(m)125+35=160(m)
Diện tích của khu đất là :
160×125=20000(m2)160×125=20000(m2)
20000m2=2ha20000m2=2ha
Đáp số: 2ha
Đề số 13 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S.
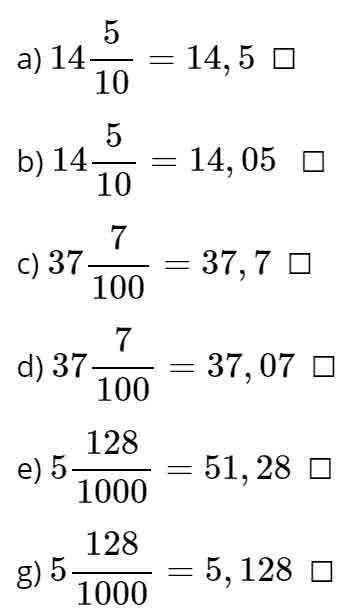
Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:
a) Viết số thích hợp vào chỗ chấm:
12 tạ 7 kg = ….. kg
A. 12007 B. 1207 C. 127
b) Viết số thích hợp vào chỗ chấm:
14156m = ….. km
A. 1,4156 B. 14,156 C.1415,6
Câu 3. Nối ba số có độ dài bằng nhau:

Câu 4. Đúng ghi Đ, sai ghi S.
a) 4,8m = 48cm ☐
b) 4,8m = 48dm ☐
c) 2,1 tấn = 2100kg ☐
d) 2,1 tấn = 210 kg ☐
Câu 5. Viết các phân số sau dưới dạng phân số thập phân và số thập phân (theo mẫu):

Lời giải
Câu 1.
Phương pháp:

Ta có kết quả như sau:
a) Đ; b) S; c) S;
d) Đ; e) S; g) Đ.
Câu 2.
Phương pháp:
a) Dựa vào cách đổi: 11 tạ =100kg

Chọn B.
Câu 3.
Phương pháp:
– Dựa vào cách chuyển đổi các đơn vị đo độ dài:


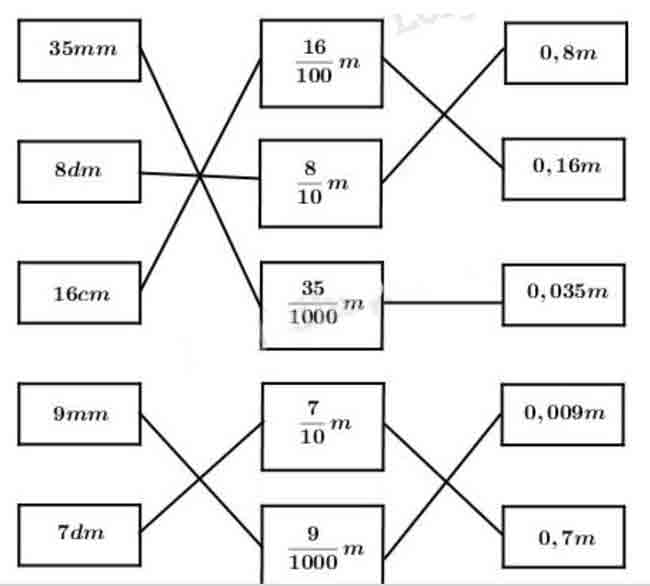
Câu 4.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:

Ta có kết quả như sau: a) S; b) Đ; c) Đ; d) S.
Câu 5.
Phương pháp:
– Nhân cả tử số và mẫu số của phân số với một số tự nhiên thích hợp để được phân số có mẫu số là 10;100;100;1000;…

– Tính diện tích trồng rau = diện tích khu đất −− ((diện tích trồng cây ăn quả ++ diện tích đào ao thả cá)).
Cách giải:
Diện tích khu đất trồng cây ăn quả là:

Câu 7.
Phương pháp:
– Viết 22 tạ 50kg50kg thành số đo có đơn vị là tạ.
– Tìm tổng khối lượng gạo nếp và gạo tẻ xe chở được.
– Khối lượng ngô = tổng khối lượng gạo nếp, gạo tẻ xe chở được −− tổng khối lượng gạo nếp và gạo tẻ.
Cách giải:

Đề số 14 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:
a) Viết thành phân số thập phân: 0,008=…?

Câu 2. Đúng ghi Đ, sai ghi S:
Điền dấu (>,=,<)(>,=,<) vào chỗ chấm :

Câu 4. Nối phân số (hoặc hỗn số) với số thập phân bằng nó:

Câu 5. Đúng ghi Đ, sai ghi S:
Số 125,08 có phần thập phân gồm có:
a) 88 phần mười b) 00 phần mười, 88 phần trăm
Câu 6. Cho 3 chữ số 1, 5, 7. Hãy lập các sô thập phân có đủ ba chữ số đã cho mà phần thập phân có hai chữ số. Xếp các số lập được theo thứ tự giảm dần.
Câu 7. Tính rồi viết kết quả dưới dạng số thập phân:
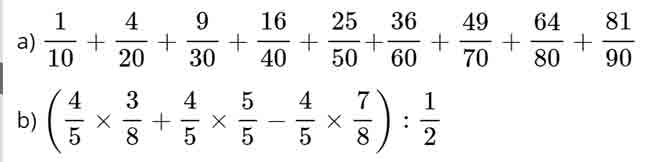
Câu 8. Viết đáp số dưới dạng số thập phân:
Hai công nhân cùng làm chung một công việc. Nếu người thứ nhất làm riêng thì làm xong trong 8 giờ. Nếu người thứ hai làm riêng thì làm xong trong 12 giờ.
Hỏi cả hai người làm chung thì sau mấy giờ xong công việc?
Lời giải
Câu 1.
Phương pháp:

Chọn C.
Câu 2.
Phương pháp:
Ta có: 1000:8=1251000:8=125. Nhân cả tử số và mẫu số của phân số

Ta có kết quả như sau: a) S; b) Đ; c) S.
Câu 3.
Phương pháp:
Để viết phân số dưới dạng hỗn số ta lấy tử số chia cho mẫu số; thương tìm được là phần nguyên, viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số mà số chia.
Cách giải:
Ta có: 208:100=2208:100=2 dư 88.


Câu 5.
Phương pháp:
– Những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
– Các chữ số ở bên phải dấu phẩy theo thứ tự từ trái sang phải lần lượt là hàng phần mười, hàng phần trăm, hang phần nghìn, …
Cách giải:
Trong số thập phân 125,08125,08 :
– Phân nguyên gồm có: 11 trăm, 22 chục, 55 đơn vị.
– Phần thập phân gồm có: 00 phần mười, 88 phần trăm.
Vậy ta có đáp án như sau: a) S; b) Đ.
Câu 6.
Phương pháp:
– Viết các số thập phân thỏa mãn yêu cầu bài toán.
– So sánh các số thập phân rồi sắp xếp theo thứ tự từ lớn đến nhỏ.
Cách giải:
Các số thập phân có đủ ba chữ số 1,5,71,5,7 mà phần thập phân có hai chữ số là:

Câu 7.
Phương pháp:
a) Rút gọn các phân số về cùng mẫu số chung là 1010 sau đó thực hiện phép cộng các phân số.
b) Biểu thức có dấu ngoặc thì ta tính trong ngoặc trước, ngoài ngoặc sau. Biểu thức chỉ có phép nhân và phép chia thì ta tính lần lượt từ trái sang phải.
Cách giải:


Câu 8.
Phương pháp:
– Coi cả công việc là 11 đơn vị.
– Tìm số phần công việc người thứ nhất (hoặc người thứ hai) làm được trong 11 giờ ta lấy 11 chia cho số giờ hoàn thành công việc đó của người thứ nhất (hoặc người thứ hai).
– Tìm số phần công việc cả hai người làm được trong 11 giờ.
– Tìm số giờ để làm xong công việc nếu hai người làm chung ta lấy 11 chia cho số phần công việc cả hai người làm được trong 11 giờ.
Cách giải:
Một giờ người thứ nhất làm đượcsố phần công việc là:

Đề số 15 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:


Câu 4. Khoanh tròn vào chữ đặt trước câu trả lời đúng:
Viết số thập phân 40,060 dưới dạng rút gọn nhất:
A. 4,6 B. 40,6
C. 40,006 D. 40,06
Câu 5. Đúng ghi Đ, sai ghi S:
Các số sau đây được xếp theo thứ tự từ bé đến lớn:


Lời giải
Câu 1.
Phương pháp:
– Nếu viết thêm chữ số 00 vào bên phải phần thập phân của một số thập phân thì được một số thập phân bằng nó.
– Nếu một số thập phân có chữ số 00 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.
Cách giải:

Chọn D.
Câu 3.
Phương pháp:
*) Nếu viết thêm chữ số 00 vào bên phải phần thập phân của một số thập phân thì được một số thập phân bằng nó.
*) Muốn so sánh hai số thập phân ta có thể làm như sau:
– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn … đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Cách giải:

Vậy ta có kết quả như sau:
a) S; b) Đ;
c) S; d) Đ.
Câu 4.
Phương pháp:
Nếu một số thập phân có chữ số 00 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.
Cách giải:
Nếu một số thập phân có chữ số 00 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.
Do đó ta có: 40,060=40,06
Chọn D.
Câu 5.
Phương pháp:
Muốn so sánh hai số thập phân ta có thể làm như sau:
– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn … đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Cách giải:
Các số thập phân đã cho có phần nguyên bằng nhau và bằng

Vậy kết quả như sau: a) S; b) Đ.
Câu 6.
Phương pháp:
Dựa vào dữ kiện đề bài và cách so sánh các số thập phân để tìm số tự nhiên thỏa mãn yêu cầu đề bài.
Cách giải:

Vậy ta có kết quả là: Đ; S.
Câu 7.
Phương pháp:
So sánh các số tự nhiên đã cho, sau đó sắp xếp theo thứ tự từ lớn đến bé.
Cách giải:
So sánh phần nguyên của các số thập phân đã cho ta có:

Câu 8.
Phương pháp:
Dựa vào dữ kiện đề bài và cách so sánh các số thập phân để tìm các số tự nhiên thỏa mãn yêu cầu đề bài.
Cách giải:




Câu 11.
Phương pháp:
– Tách mẫu số thành tích của các thừa số, sau đó lần lượt chia tử số và mẫu số cho các thừa số chung.
– Viết phân số tìm được dưới dạng phân số thập phân rồi viết dưới dạng số thập phân.
Cách giải:
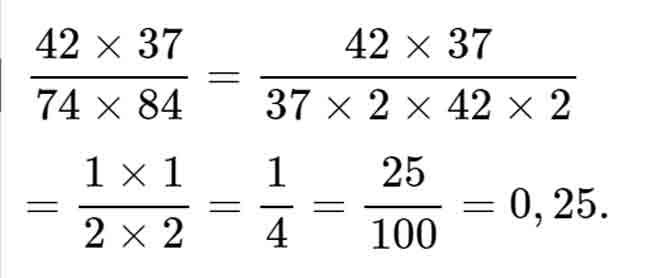
Đề số 16 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:



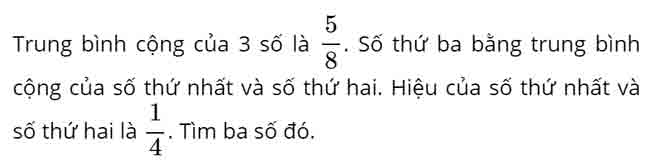
Lời giải
Câu 1.
Phương pháp:
Nếu một số thập phân có chữ số 00 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.
Cách giải:
Nếu một số thập phân có chữ số 00 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.



Câu 4.
Phương pháp:
So sánh các số tự nhiên đã cho, sau đó sắp xếp theo thứ tự từ bé đến lớn.
Cách giải:
Các số thập phân đã cho đều có phần nguyên là 0.
So sánh hàng phần mười của các số thập phân đã cho ta có:

Vậy kết quả như sau: a) S; b) Đ.
Câu 5.
Phương pháp:
Muốn so sánh hai số thập phân ta có thể làm như sau:
– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn … đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Cách giải:

phần thập phân của một số thập phân thì được một số thập phân bằng nó.).
Ta có kết quả như sau:
a) S; b) Đ;
c) S; d) Đ.
Câu 6.
Phương pháp:
Áp dụng các quy tắc:
– Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
– Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
– Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
– Muốn tìm số bị chia ta lấy thương nhân với số chia.
Cách giải:
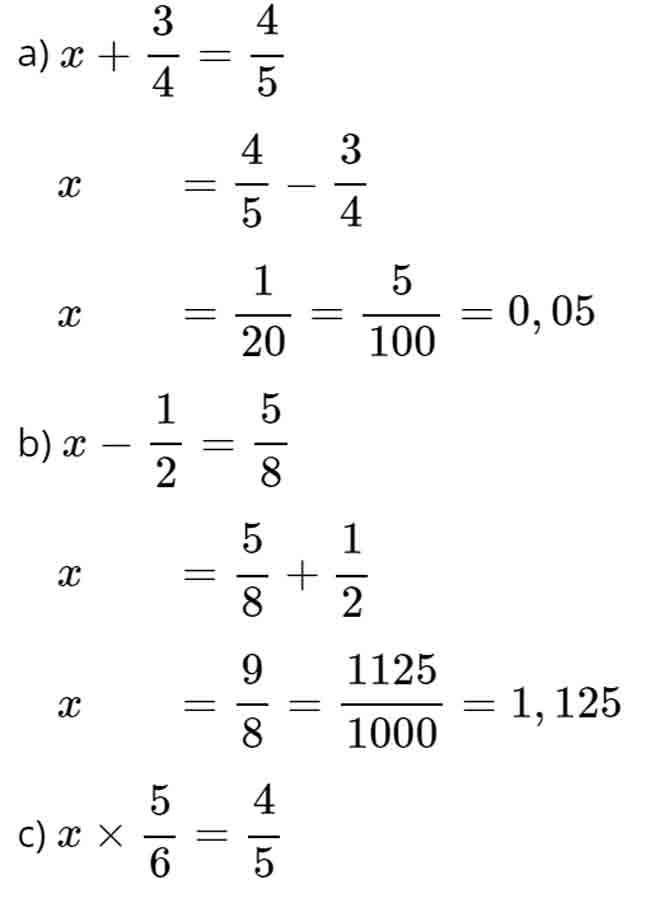


Câu 8.
Phương pháp:
– Vẽ sơ đồ biểu diễn trung bình cộng dựa vào ba số.
– Số thứ ba bằng trung bình cộng của số thứ nhất và số thứ hai nên số thứ ba bằng trung bình cộng của cả ba số. Từ đó tìm được số thứ ba.


Số thứ hai là : 0,5 ;
Số thứ ba là : 0,625.
Đề số 17 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng chọn Đ, sai chọn S :



Hỏi diện tích khu vườn đó là bao nhiêu héc-ta?
A. 70ha B.700ha C.7000ha
Câu 6. Một xe máy trung bình mỗi phút đi được 600m. Hỏi:
a) Mỗi giờ xe máy đi được bao nhiêu ki-lô-mét?
b) Xe máy đi được 21km 600m thì hết bao nhiêu phút?
Câu 7. Bốn con bò ăn hết một tạ cỏ trong một ngày. Hỏi 2 con bò như thế trong 30 ngày ăn hết bao nhiêu tấn cỏ?
Câu 8. Một khu đất hình vuông có chu vi là 1km. Hỏi diện tích khu đất đó là bao nhiêu héc-ta?
Lời giải
Câu 1.
Phương pháp:
– Viết các số đo dưới dạng hỗn số sau đó viết dưới dạng số thập phân.
– Áp dụng cách chuyển đổi các đơn vị đo độ dài:










Đề số 18 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài


và 0,06kg.
Hỏi 48 bánh xà phòng như thế nặng bao nhiêu ki-lô-gam?
Câu 7. Một khu rộng hình chữ nhật có chu vi là 360m. Chiều
chiều dài.
a) Diện tích thửa ruộng là bao nhiêu héc-ta?
b) Người ta cấy lúa trung bình 100m2 thì thu hoạch được 75kg thóc. Hỏi trên thửa ruộng đó người ta thu hoạch được bao nhiêu tấn thóc?
Lời giải
Câu 1.
Phương pháp:
– Viết các số đo dưới dạng phân số hoặc hỗn số sau đó viết dưới dạng số thập phân.
– Áp dụng cách chuyển đổi các đơn vị đo độ dài:

Ta có kết quả như sau:
a) S; b) Đ; c) Đ;
d) S; e) S; g) Đ.
Câu 2.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:


Câu 5.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:
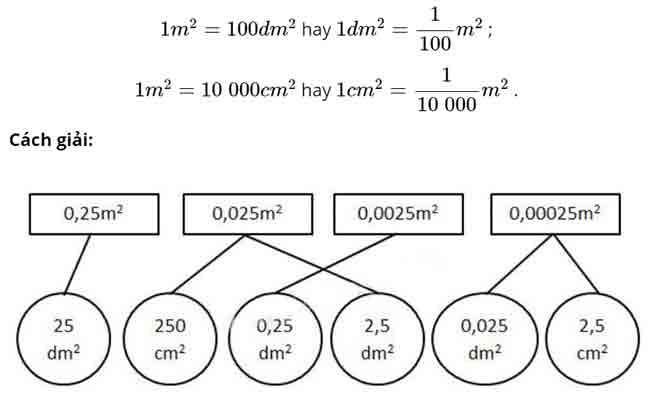
Câu 6.
Phương pháp:


Cách giải:
a)
Nửa chu vi thửa ruộng là:

Số thóc thu hoạch được trên thửa ruộng là:

Đề số 19 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:

Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:


Lời giải
Câu 1.
Phương pháp:
Muốn cộng hai số thập phân ta làm như sau:
– Viết số hạng này dưới số hạng kia làm sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
– Cộng như cộng các số tự nhiên.
– Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.
Cách giải:
Ta đặt tính và thực hiện tính như sau:

Ta có kết quả như sau:
a) S, Đ; b) S , Đ.
Câu 2.
Phương pháp:
Cách 1: Áp dụng tính chất giao hoán của phép cộng các số thập phân :
Khi đổi chỗ hai số hạng trong một tổng thì tổng không thay đổi.
a+b=b+a
Cách 2: Tính giá trị hai phép tính rồi so sánh kết quả với nhau.
Cách giải:
(Giải theo cách 1: áo dụng tính chất giao hoán)
Phép cộng các số thập phân có tính chất giao hoán: Khi đổi chỗ hai số hạng trong một tổng thì tổng không thay đổi.
a+b=b+a
Do đó:
a) 28,5+1,64=1,64+28,5
Ta có kết quả như sau: S, Đ, S.
b) 264+43,25=43,25+264
Ta có kết quả như sau: S, S, Đ.
Câu 3.
Phương pháp:
*) Muốn cộng hai số thập phân ta làm như sau:
– Viết số hạng này dưới số hạng kia làm sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
– Cộng như cộng các số tự nhiên.
– Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.
*) Nếu có số đo đơn vị thì sau khi tính ta ghi thêm đơn vị vào sau kết quả tính.
Cách giải:
a) Ta đặt tính và thực hiện tính như sau:

Chọn A.
Câu 4.
Phương pháp:
Để tính tổng nhiều số thâp phân ta làm tương tự như tính tổng hai số thập phân.
Cách giải:
a) Ta đặt tính và thực hiện tính như sau:

Chọn B.
Câu 5.
Phương pháp:
– Tính số tấn hàng xe thứ hai chở được == số tấn hàng xe thứ nhất chở +1,2 tấn.
– Tính số tấn hàng xe thứ ba chở được == số tấn hàng xe thứ hai chở +0,6 tấn.
– Số tấn hàng cả 33 xe chở == số tấn hàng xe thứ nhất chở ++ số tấn hàng xe thứ hai chở ++ số tấn hàng xe thứ ba chở.
Cách giải:
Xe thứ hai chở được số tấn hàng là:



Đáp số: 80m.
🔢 GIA SƯ TOÁN
Đề số 20 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:



Câu 8. Cho ba chữ số 4;5;6
a) Hãy viết tất cả các số thập phân có 3 chữ số khác nhau.
b) Tính tổng các số viết được ở câu a) bằng cách thuận tiện nhất.
Lời giải
Câu 1.
Phương pháp:

Chọn D.
Câu 2.
Phương pháp:
– Cách 1: Biểu thức chỉ có phép cộng thì ta thực hiện lần lượt từ trái sang phải.
– Cách 2: Áp dụng tính chất giao hoán và kết hợp của phép cộng để nhóm các số có tổng là số tự nhiên lại với nhau.
Cách giải:

Ta có kết quả như sau: A. S; B. S; C. Đ; D. S.
Câu 3.
Phương pháp:
Đổi các số đo khối lượng về cùng đơn vị đo là yến, sau đó thực hiện phép cộng các số thập phân như thông thường.
Cách giải:

Chọn C.
Câu 4.
Phương pháp:
Muốn cộng hai số thập phân ta làm như sau:
– Viết số hạng này dưới số hạng kia làm sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
– Cộng như cộng các số tự nhiên.
– Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.
Cách giải:
Ta đặt tính và thực hiện tính như sau:
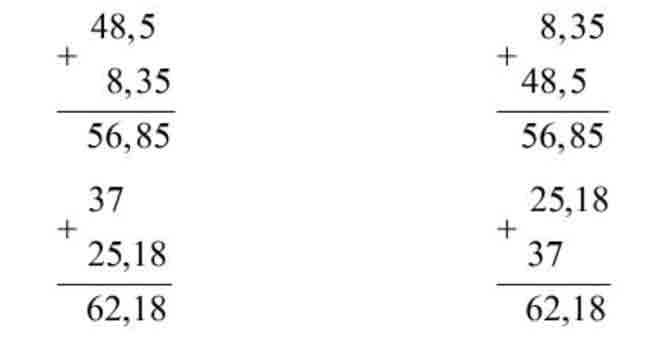
Ta có kết quả như sau:
a) S; b) Đ; c) Đ; d) S.
Câu 5.
Phương pháp:






Đề số 21 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:


Câu 4. Đúng ghi Đ, sai ghi S :
Câu 5. Khoanh tròn vào chữ đặt trước câu trả lời đúng:
Một người đi xe đạp trong 3 giờ. Giờ thứ nhất đi được 13,5km. Giờ thứ hai người đó đi kém giờ thứ nhất 1,8km nhưng nhiều hơn giờ thứ ba 1,25km.
Hỏi giờ thứ ba người đó đi được bao nhiêu ki-lô-mét?
A. 9,45km B. 10,45km C. 10,55km
Câu 6. Tính bằng cách thuận tiện nhất

Câu 7. Một người thợ trong ba ngày dệt được tất cả 58,35m vải. Ngày thứ nhất người thợ đó dệt được 18,75m. Ngày thứ hai dệt hơn ngày thứ nhất 0,8m. Hỏi ngày thứ ba người thợ đó dệt được bao nhiêu mét vải?
Câu 8. Tổng của ba số bằng 7. Tổng của số thứ nhất và số thứ hai bằng 3,77. Tổng của số thứ hai và số thứ ba bằng 5,58. Tìm ba số đó.
Lời giải
Câu 1.
Phương pháp:
Muốn trừ một số thập phân cho một số thập phân ta làm như sau:
– Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột nhau.
– Thực hiện phép trừ như trừ các số tự nhiên.
– Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
Chú ý: Nếu số chữ số ở phần thập phân của số bị trừ ít hơn số chữ số ở phần thập phân của số trừ, thì ta có thể viết thêm một số thích hợp chữ số 00 vào bên phải phần thập phân của số bị trừ, rồi trừ như trừ các số tự nhiên.
Cách giải:
a) Ta đặt tính và thực hiện tính như sau:

Vậy kết quả lần lượt là: S; Đ.
Câu 2.
Phương pháp:
Muốn trừ một số thập phân cho một số thập phân ta làm như sau:
– Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột nhau.
– Thực hiện phép trừ như trừ các số tự nhiên.
– Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
Chú ý: Nếu số chữ số ở phần thập phân của số bị trừ ít hơn số chữ số ở phần thập phân của số trừ, thì ta có thể viết thêm một số thích hợp chữ số 00 vào bên phải phần thập phân của số bị trừ, rồi trừ như trừ các số tự nhiên.
Cách giải:
a) Ta đặt tính và thực hiện tính như sau:

Vậy kết quả lần lượt là: S; Đ.
Câu 3.
Phương pháp:
Áp dụng các quy tắc:
a) Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
b) Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
Cách giải:

Chọn B.
Câu 4.
Phương pháp:
– Cách 1: Biểu thức chỉ có phép trừ thì ta tính lần lượt từ trái sang phải.

Câu 5.
Phương pháp:
– Tính số ki-lô-mét đi được trong giờ thứ hai ta lấy số ki-lô-mét đi được trong giờ thứ nhất trừ đi 1,8km (vì giờ thứ hai người đó đi kém giờ thứ nhất 1,8km).
– Tính số ki-lô-mét đi được trong giờ thứ ba ta lấy số ki-lô-mét đi được trong giờ thứ hai trừ đi 1,25km1,25km (Vì giờ thứ hai người đó đi nhiều hơn giờ thứ ba 1,25km).
Cách giải:
Giờ thứ hai người đó đi được số ki-lô-mét là:


Câu 7.
Phương pháp:
– Tính số mét vải người thợ dệt được trong ngày thứ hai ta lấy số số mét vải người thợ dệt được trong ngày thứ nhất cộng với 0,8m.
– Tính tổng số mét vải dệt được trong hai ngày đầu.
– Tính số mét vải người thợ dệt được trong ngày thứ ba ta lấy số mét vải người thợ dệt được trong cả ba ngày trừ đi số mét vải người thợ dệt được trong hai ngày đầu.
Cách giải:
Ngày thứ hai người thợ đó dệt được số mét vải là:
18,75+0,8=19,55(m)Ngày thứ nhất và ngày thứ hai người thợ đó dệt được số mét vải là:18,75+19,55=38,3(m)Ngày thứ ba người thợ đó dệt được số mét vải là:
58,35–38,3=20,05(m)
Đáp số: 20,05m
Câu 8.
Phương pháp:
– Tìm số thứ nhất = tổng của ba số− tổng của số thứ hai và số thứ ba.
– Tìm số thứ hai = tổng của số thứ nhất và số thứ hai − số thứ nhất.
– Tìm số thứ ba = tổng của số thứ hai và số thứ ba − số thứ hai.
Cách giải:
Số thứ nhất là :
7–5,58=1,42
Số thứ hai là :
3,77–1,42=2,35
Số thứ ba là :
5,58–2,35=3,23
Đáp số: Số thứ nhất: 1,42;
Số thứ hai: 2,35;
Số thứ ba: 3,23.
Đề số 22 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S :
a) Tổng hai số thập phân không thể là số tự nhiên ☐
b) Tổng hai số thập phân có thể là số thập phân hoặc số tự nhiên ☐
c) Hiệu hai số thập phân không thể là số tự nhiên ☐
d) Hiệu hai số thập phân có thể là số thập phân hoặc số tự nhiên ☐
Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng:
Tính: 48,75−8,75−12,5−7,5=?
A. 60 B. 42
C. 24 D. 20
Câu 3. Đúng ghi Đ, sai ghi S :
a) 36–4,5+1,5
=36–(4,5+1,5)
=36–6
=30 ☐
b) 36−4,5+1,5
=36−(4,5–1,5)
=36−3
=33 ☐
Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng:
Một số thêm 2,1 thì bằng 1,5 thêm 3,4. Hãy tìm số đó.
A. 4,9 B. 0,6
C. 1,9 D. 2,8
Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:
Trung bình cộng của 3 số là 12. Số thứ nhất là 12,5. Số thứ hai là 12,3. Tìm số thứ ba.
A. 10,2 B. 11,2 C. 13,2
Câu 6. Tính bằng cách thuận tiện nhất:
a) 68,75−23,36−16,64
b) 46−38,29+18,29 ;
c) 18,71−9,24+16,29−6,76.
Câu 7. Tìm x, biết:
a)41,75+x+27,3=100,5 b)x+27,9−93,7=48,75
Câu 8. Tổng của hai số là 19,1. Nếu giảm số hạng thứ nhất đi 4 lần và giữ nguyên số hạng thứ hai thì được tổng mới là 7,4. Tìm hai số đó.
Lời giải
Câu 1.
Phương pháp:
– Đọc kĩ các phát biểu và xác đinh tính đúng, sai của các phát biểu đó.
– Có thể lấy ví dụ để hiểu rõ hơn
Cách giải:
– Tổng hai số thập phân có thể là số thập phân hoặc số tự nhiên.
Ví dụ: 1,5+2,26=3,76 ; 4,4+5,6=10.
Hiệu hai số thập phân có thể là số thập phân hoặc số tự nhiên.
Ví dụ: 7,9−4,3=3,6 ; 15,6−8,6=7.
Vậy ta có kết quả như sau:
a) S; b) Đ; c) S; d) Đ.
Câu 2.
Phương pháp:
– Cách 1: Biểu thức chỉ có phép trừ nên ta tính lần lượt từ trái sang phải.
– Cách 2: Áp dụng công thức a−b−c−d=(a−b)−(c+d) để tính bằng cách thuận tiện.
Cách giải:
48,75−8,75−12,5−7,5
=(48,75−8,75)−(12,5+7,5)
=40−20=20
Chọn D.
Câu 3.
Phương pháp:
Áp dụng công thức a−b−c=a−(b+c) để tính bằng cách thuận tiện.
Cách giải:
36−4,5+1,5
=36−(4,5–1,5)
=36−3
=33
Vậy ta có kết quả như sau: a) S; b) Đ.
Câu 4.
Phương pháp:
– Tính tổng của hai số 1,5 và 3,4 .
– Tính số cần tìm ta lấy tổng của hai số 1,5 và 3,4 trừ đi 2,1.
Cách giải:
Tổng của hai số 1,5 và 3,4 là:
1,5+3,4=4,9
Số cần tìm là:
4,9−2,1=2,8
Chọn D.
Câu 5.
Phương pháp:
– Tìm tổng của 3 số = trung bình cộng của 3 số ×3.
– Tìm số thứ ba = tổng của 3 số − tổng của số thứ nhất và số thứ hai.
Cách giải:
Tổng của 33 số đó là:
12×3=36
Số thứ ba là:
36−(12,5+12,3)=11,2
Chọn B.
Câu 6.
Phương pháp:
Áp dụng các công thức:
+) a−b−c=a−(b+c) ;
+) a−b+c=a−(b−c);
+) a−b+c−d=(a+c)−(b+d)
Cách giải:
a) 68,75−23,36−16,64
=68,75−(23,36+16,64)
=68,75−40
=28,75
b) 46−38,29+18,29
=46−(38,29−18,29)
=46−20
=26
c) 18,71−9,24+16,29−6,76
=(18,71+16,29)−(9,24+6,76)
=35−16
=19.
Câu 7.
Phương pháp:
Áp dụng quy tắc: Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
Cách giải:
a) 41,75+x+27,3=100,5
41,75+27,3+x=100,5
69,05+x=100,5
x=100,5−69,05
x=31,45
b) x+27,9−93,7=48,75
x+27,9=48,75+93,7
x+27,9=142,45
x=142,45−27,9
x=114,55.
Câu 8.
Phương pháp:
– Vẽ sơ đồ dựa vào đề bài đã cho.
– Quan sát sơ đồ và lập luận để tìm số thứ nhất.
– Tìm số thứ hai = tổng của hai số − số thứ nhât.
Cách giải:
Theo đề bài ta có sơ đồ:

Vì giảm số hạng thứ nhất đi 4 lần và giữ nguyên số hạng thứ

hạng thứ nhất là:
19,1−7,4=11,7
Số hạng thứ nhất là :
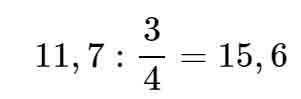
Số hạng thứ hai là :
19,1−15,6=3,5
Đáp số: Số thứ nhất: 15,6;
Số thứ hai: 3,5.
Đề số 23 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng chọn Đ, sai chọn S:
a) 3,45×9=31,05 ☐
3,45×9=3,105 ☐
b) 40,08×25=100,2 ☐
40,08×25=1002 ☐
Câu 2. Đúng chọn Đ, sai chọn S:

Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:
Một số nếu giảm đi 5 lần rồi bớt đi 32,5 thì được 41,72. Tìm số đó.
A. 370,1 B. 371,1 C. 4,211
Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng:
Tìm x trong các số tự nhiên 1,2,3,4 để có 2,5×x>72,5×x>7
A. x=1 B. x=2
C. x=3 D. x=4
Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:
Một mảnh vườn hình chữ nhật có chiều rộng 7,24m. Chiều
rộng bằng

chiều dài. Tính chu vi mảnh vườn đó.
A. 56,92m B. 57,82m C. 57,92m
Câu 6. Một ô tô trung bình mỗi giờ đi được 42,6km.
a) Trong 3 giờ ô tô đi được bao nhiêu ki-lô-mét?
b) Ô tô đi quãng đường từ tỉnh A đến tỉnh B hết

giờ. Hỏi từ tỉnh A đến tỉnh B dài bao nhiêu ki-lô-mét?
Câu 7. Một chai nước chứa được 0,75 lít nước. Một lít nước nặng 1,05kg. Mỗi vỏ chai nặng 0,2kg. Hỏi 24 chai đựng đầy nước như vậy nặng tất cả bao nhiêu ki-lô-gam?
Câu 8. Tính nhanh biểu thức sau:
(1,25−0,25×5)×(1,1×1,2×1,3×1,4×1,5)
Lời giải
Câu 1.
Phương pháp:
Muốn nhân một số thập phân với một số tự nhiên ta làm như sau:
– Nhân như nhân các số tự nhiên.
– Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Cách giải:
a) Ta đặt tính và thực hiện tính như sau:

Vậy kết quả lần lượt là: S; Đ.
Câu 2.
Phương pháp:
Muốn nhân một số thập phân với một số tự nhiên ta làm như sau:
– Nhân như nhân các số tự nhiên.
– Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Cách giải:
Ta đặt tính và thực hiện tính như sau:

Vậy kết quả lần lượt là: a) S; b) Đ.
Câu 3.
Phương pháp:
Giả sử x là số cần tìm. Theo đề bài ta có: x:5−32,5=41,72. Giải bài toán tìm x như thông thường ta tìm được số đó.
Cách giải:
Giả sử xx là số cần tìm. Theo đề bài ta có: x:5−32,5=41,72
x:5−32,5=41,72
x:5=41,72+32,5x:5=74,22
x=74,22×5
x=371,1
Vậy số cần tìm là 371,1.
Chọn B.
Câu 4.
Phương pháp:
Thay lần lượt các giá trị của x rồi tính giá trị biểu thức 2,5×x
, sau đó so sánh kết quả với 7.
Cách giải:
Ta có:
2,5×1=2,5 ; 2,5<7
2,5×2=5 ; 5<7
+) 2,5×3=7,5 ; 7,5>7.
+) 2,5×4=10 ; 10>7.
Vậy trong các số tự nhiên 1,2,3,4 để có 2,5×x>7 thì x=3 hoặc x=4.
Chọn C và D.
Câu 5.
Phương pháp:
– Tính chiều dài mảnh vườn ta có thể lấy chiều rộng chia cho 1 rồi nhân với 3.
– Tính chu vi = (chiều dài + chiều rộng) ×2.
Cách giải:
Chiều dài của mảnh vườn đó là:
7,24:1×3=21,72(m)Chu vi mảnh vườn đó là:
(7,24+21,72)×2=57,92(m)Đáp số: 57,92m
Chọn C.
Câu 6.
Phương pháp:

– Tính số ki-lô-mét ô tô đi được trong 3 giờ ta lấy số ki-lô-mét ô tô đi được trong 1 giờ nhân với 3.
– Tính độ dài từ tỉnh A đến tỉnh B ta lấy số mét đường ô tô đi được trong 1 giờ nhân với số giờ đi hết quãng đường đó, sau đó đổi sang đơn vị đo là ki-lô-mét.
Cách giải:

Câu 7.
Phương pháp:
– Tính số lít nước có trong 24 chai = số lít nước có trong 1 chai ×24.
– Tính cân nặng của 24 vỏ chai =
cân nặng của 1 vỏ chai ×24.
– Tính cân nặng của 24 chai đựng đầy nước =
cân nặng của lượng nước có trong 24 chai + cân nặng của 24 vỏ chai.
Cách giải:
Số lít nước trong 24 chai là:
0,75×24=18 (lít)
18 lít nước nặng số ki-lô-gam là :
1,05×18=18,9(kg)
24 vỏ chai nặng số ki-lô-gam là:
0,2×24=4,8(kg)
24 chai nước nặng số ki-lô-gam là :
18,9+4,8=23,7(kg)
Đáp số: 23,7kg.
Lưu ý: Có thể tính cân nặng của 11 chai đầy nước bằng cách tính tổng cân nặng của 0,750,75 lít nước và cân nặng của 11 vỏ chai. Sau đó để tính cân nặng của 2424 chai đựng đầy nước ta lấy cân nặng của 11 chai đầy nước nhân với 2424.
Câu 8.
Phương pháp:
Tính giá trị của biểu thức trong ngoặc trước, sau đó tính giá trị biểu thức đã cho.
Cách giải:
(1,25−0,25×5)×(1,1×1,2×1,3×1,4×1,5)
=(1,25−1,25)× (1,1×1,2×1,3×1,4×1,5)
=0×(1,1×1,2×1,3×1,4×1,5)
=0 (Vì 0 nhân với số nào cũng bằng 0)
Đề số 24 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng chọn Đ, sai chọn S:
a) 0,84×125=10,5 ☐
b) 0,84×125=105 ☐
c) 0,025×204=51 ☐
d) 0,025×204=5,1 ☐
Câu 2. Khoanh vào chữ số trước câu trả lời đúng:
Tính 0,32 tấn × 125 + 1,2 tạ × 15 – 3,6 tấn × 0,25 = ?
A. 40,8 tạ B. 40,8 tấn
C. 40,9 tấn D. 39,9 tấn
Câu 3. Nối câu trả lời với đáp số đúng:
Một người đi xe máy trung bình mỗi phút đi được 0,605km. Hỏi người đó đi được bao nhiêu mét trong một thời gian sau:

Câu 4. Đúng chọn Đ, sai chọn S:
Điền dấu (>,=,<) vào chỗ chấm:
6,25×400…..62,5×40
a) 6,25×400>62,5×40
b) 6,25×400=62,5×40
c) 6,25×400<62,5×40
Câu 5. Khoanh vào chữ số trước câu trả lời đúng:
Một tờ bìa hình vuông có diện tích là 1,44m21,44m2. Hỏi chu vi tờ bìa là bao nhiêu mét?
A. 3,8m B. 4,8m C. 8,4m

Câu 7. Tính giá trị biểu thức bằng cách thuận tiện nhất:
a) 2,5×9,5×4+19,5×10
b) 5,25×18−5,25×2−5,25×6
Câu 8. 0,25 chiều rộng của mảnh vườn là 3,75m. Chiều dài mảnh vườn gấp 2,5 lần chiều rộng. Người ta cấy lúa thí điểm cứ 1m2 thu được 0,8kg. Hỏi số thóc thu hoạch trên mảnh vườn đó bao nhiêu tấn?Lời giải
Câu 1.
Phương pháp:
Muốn nhân một số thập phân với một số tự nhiên ta làm như sau:
– Nhân như nhân các số tự nhiên.
– Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Cách giải:
Ta đặt tính và thực hiện tính như sau:
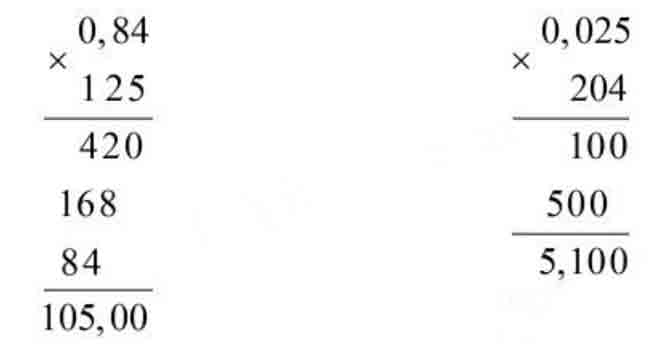
Vậy kết quả lần lượt như sau: a) S; b) Đ; c) S; d) Đ.
Câu 2.
Phương pháp:
Đổi 1,2 tạ =0,12 tấn, sau đó thực hiện tính giá trị biểu thức như thông thường. Biểu thức có các phép tính cộng, trư, nhân, chia thì ta thực hiện phép nhân, chia trước, thực hiện phép cộng, trừ sau.
Cách giải:
0,32 tấn ×125 +1,2 tạ ×15 −3,6 tấn ×0,25
=0,32 tấn ×125 +0,12 tấn ×15 −3,6 tấn ×0,25
=40 tấn +1,8 tấn −0,9 tấn
=41,8 tấn −0,9 tấn
=40,9 tấn
Chọn C.
Câu 3.
Phương pháp:
– Đổi: 0,605km=605m và đổi các số đo thời gian từ đơn vị giờ sang số đo có đơn vị là phút.
– Tính số mét đường người đó đi được ta lấy số mét đi được trong 11 phút nhân với thời gian đi.
Cách giải:
Đổi: 0,605km=605m;

Ta có kết quả như sau:
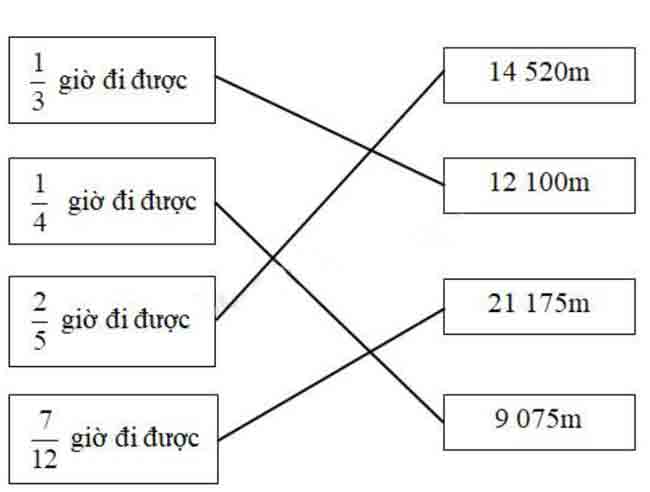
Câu 4.
Phương pháp:
Thực hiện tính kết quả hai vế rồi so sánh với nhau.
Cách giải:
Ta có: 6,25×400=2500 ; 62,5×40=2500
Mà: 2500=2500
Do đó: 6,25×400=62,5×40.
Vậy ta có kết quả như sau: a) S; b) Đ; c) S.
Câu 5.
Phương pháp:
– Đổi: 1,44m2=144dm2.
– Dựa vào diện tích hình vuông để lập luận tìm độ dài cạnh tờ bìa hình vuông.
– Tính chu vi = cạnh ×4.
– Đổi số đo vừa tìm được sang đơn vị đo là mét.
Cách giải:
Đổi: 1,44m2=144dm2.
Ta có 12×12=144 nên độ dài cạnh của tờ bìa hình vuông là 12dm12dm.
Chu vi của tờ bìa đó là:
12×4=48(dm)
48dm=4,8m
Đáp số: 4,8m.
Chọn B.
Câu 6.
Phương pháp:

Câu 7.
Phương pháp:
Áp dụng các công thức:
a×b+a×c=a×(b+c) ;
a×b−a×c−a×d=a×(b−c−d) ;
Cách giải:
a) 2,5×9,5×4+19,5×10
=2,5×4×9,5+10×19,5
=10×9,5+10×19,5
=10×(9,5+19,5)
=10×29=290
b) 5,25×18−5,25×2−5,25×6
=5,25×(18−2−6)
=5,25×10=52,5.
Câu 8.
Phương pháp:


Đề số 25 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng chọn Đ, sai chọn S:

Câu 2. Nối phép nhân với kết quả của phép nhân đó:

Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:
57,48×0,8594+42,52×0,8594
A. 8,594 B. 85,94 C. 859,4
Câu 4. Đúng chọn Đ, sai chọn S:
Một xe máy trung bình mỗi giờ đi được 36,4km. Hỏi trong 3 giờ 15 phút ô tô đi được bao nhiêu ki-lô-mét?
a) 3 giờ 15 phút = 3,15 giờ
36,4×3,15=114,66 (km) ☐
b) 3 giờ 15 phút = 3,25 giờ
36,4×3,25=118,3 (km) ☐
Câu 5. Tính bằng cách thuận tiện nhất:
a) 2×24,36×0,5=
b) 4×42,8×0,25=
c) 0,125×9,6×8=
Câu 6. Tìm x, biết:
a) x×2,8+x×5,2=48
b) x×12,6−x×5,6=42
c) x×12,25−x+x×2,75=1050
Câu 7. Một vườn cây hình bình hành có chiều cao là 16,4m, độ dài đáy gấp rưỡi chiều cao.
a) Tính diện tích vườn đó.
b) Người ta chia mảnh vườn thành 2 khu: khu trồng cây ăn quả có diện tích lớn hơn khu trồng rau xanh là 13,44m2. Tính diện tích mỗi khu.
Lời giải
Câu 1.
Phương pháp:
Muốn nhân một số thập phân với một số thập phân ta làm như sau:
– Nhân như nhân các số tự nhiên.
– Đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Cách giải:
Ta đặt tính và thực hiện tính như sau:

Vậy kết quả lần lượt là: a) S; b) Đ; c) Đ; d) S.
Câu 2.
Phương pháp:
Khi nhân một số thập phân với 0,1;0,01;0,001;…ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Cách giải:
Khi nhân một số thập phân với 0,1;0,01;0,001;…0,1;0,01;0,001;…ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Do đó ta có:
40,02×0,1=4,002; 400,2×0,001=0,4002
40,02×0,01=0,4002; 400,2×0,01=4,002
40,02×0,001=0,04002; 400,2×0,1=40,02
Vậy kết quả như sau:
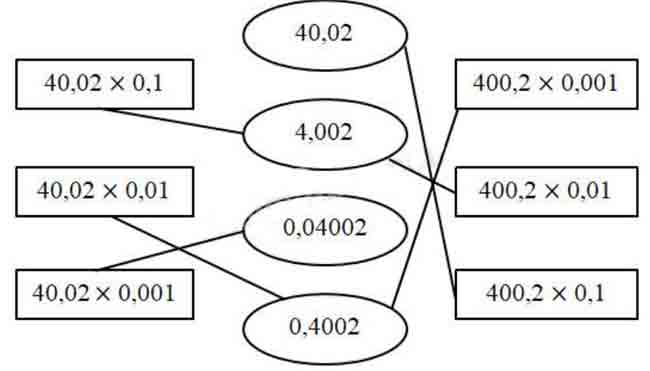
Câu 3.
Phương pháp:
– Áp dụng tính chất nhân một số với một tổng a×(b+c)=a×b+a×c để tính bằng cách thuận tiện nhất.
– Muốn nhân một số thập phân với 100 ta chỉ việc chuyển dấu phẩy của số đó sang bên phải hai chữ số.
Cách giải:
57,48×0,8594+42,52×0,8594
=(57,48+42,52)×0,8594
=100×0,8594
=85,94
Chọn B.
Câu 4.
Phương pháp:
– Đổi: 33 giờ 15 phút =3,25 giờ (vì 1 giờ =60 phút).
– Để tính quãng đường đi được trong 3 giờ 15 phút ta lấy quãng đường đi được trong 1 giờ nhân với thời gian đi.
Cách giải:
Đổi: 33 giờ 15 phút =3,25 giờ (vì 1 giờ =60 phút).
Trong 3 giờ 15 phút (hay =3,25 giờ) ô tô đi được số ki-lô-mét là:
36,4×3,25=118,3(km)
Vậy ta có kết quả là: a) S; b) Đ.
Câu 5.
Phương pháp:
Áp dụng tính chất giao hoán và kết hợp của phép nhân để nhóm các số có tích là số tự nhiên lại với nhau.
Cách giải:
a) 2×24,36×0,5
=0,5×2×24,36
=1×24,36=24,26
b) 4×42,8×0,25
=0,25×4×42,8
=1×42,8=42,8
c) 0,125×9,6×8
=8×0,125×9,6=
=1×9,6=9,6
Câu 6.
Phương pháp:
– Áp dụng tính chất nhân một số với một tổng hoặc nhân một số với một hiệu:
a×(b+c)=a×b+a×ca×(b+c)=a×b+a×c ;
– Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
Cách giải:
a) x×2,8+x×5,2=48
x×(2,8+5,2)=48
x×8=48
x=48:8
x=6
b) x×12,6−x×5,6=42
x×(12,6−5,6)=42
x×7=42
x=42:7
x=6
c) x×12,25−x+x×2,75=1050
x×12,25−x×1+x×2,75=1050
x×(12,25−1+2,75)=1050
x×14=1050
x=1050:14
x=75.
Câu 7.
Phương pháp:
– Đáy gấp rưỡi chiều cao nghĩa là đáy bằng 1,5 lần chiều cao. Để tìm độ dài đáy ta lấy chiều cao nhân với 1,5
– Tính diện tích vườn cây hình bình hành ta lấy độ dài đáy nhân với chiều cao.
– Tìm diện tích mỗi khu theo bài toán tìm hai số khi biết tổng và hiệu của hai số đó:
Số lớn = (Tổng + Hiệu) :2 ; Số bé = (Tổng – Hiệu) :2.
Cách giải:
Đáy gấp rưỡi chiều cao nghĩa là đáy bằng 1,5 lần chiều cao.
Độ dài đáy của vườn cây là :
16,4×1,5=24,6(m)
a) Diện tích vườn cây là:
24,6×16,4=403,44(m2)
b) Diện tích khu trồng rau là:
(403,44−13,44):2=195(m2)
Diện tích khu trồng cây là:
195+13,44=208,44(m2)
Đáp số: a) 403,44m2;
b) 208,44m2;195m2.
Đề số 26 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:
Tìm x, biết:
a) 7,3×x+x×2,7−x=405
x=40 ☐
x=40,5 ☐
x=45 ☐

Câu 2. Đúng ghi Đ, sai ghi S:
A. Thực hiện phép tính khi đổi tên đơn vị
3180 mm = ……… m
a) 0,001m×3180=3,180m ☐
b) 3180mm×0,001=3,180m ☐
B. Thực hiện phép tính khi đổi tên đơn vị
1500 m2 = ………. ha
a) 1500m2×0,0001=0,15ha ☐
b 0,0001ha×1500=0,15ha ☐
Câu 3. Đúng ghi Đ, sai ghi S:
a) 25+2,18×5
=2,18+25×5
=2,18+125
=127,18 ☐
b) 25+2,18×5
=27,18×5
=135,90 ☐
c) 25+2,18×5
=25+10,90
=35,9 ☐
Câu 4. Khoanh vào chữ đặt trước câu trả lời đúng:
Có 24 chai đựng dầu hỏa, mỗi chai chứa 0,75l dầu. Mỗi lít dầu hỏa nằng 0,76kg. Mỗi vỏ chai nặng 0,25kg.
Hỏi 24 chai dầu hỏa cân nặng bao nhiêu ki-lô-gam?
A. 18kg B. 19,68kg C. 20,4kg
Câu 5. Tính bằng cách thuận tiện nhất:
a) 2×4×8×0,5×0,125×(0,4321+0,5679)
b) 3,7×3,8+8,3×3,7−0,4×3,7×5

Câu 7. Một ô tô đi từ A đến B hết 3 giờ. Giờ thứ nhất đi nhiều hơn mức trung bình của cả 3 giờ là 5,45km. Giờ thứ hai đi ít hơn mức trung bình của cả 3 giờ là 4,15km. Giờ thứ ba đi được 48,75km. Hỏi quãng đường AB dài bao nhiêu ki-lô-mét?
Lời giải
Câu 1.
Phương pháp:
– Áp dụng tính chất nhân một số với một tổng hoặc nhân một số với một hiệu:
a×(b+c)=a×b+a×c ; a×(b−c)=a×b−a×c
– Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
Cách giải:
a) 7,3×x+x×2,7−x=405
x×7,3+x×2,7−x×1=405
x×(7,3+2,7−1)=405
x×9=405
x=405:9
x=45
Vậy kết quả lần lượt là: S; S; Đ.

Vậy kết quả lần lượt là: S; S; Đ.
Câu 2.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:

Cách giải:
A. Phép tính khi đổi tên đơn vị 3180mm=…m là:
0,001m×3180=3,180m
Vậy kết quả lần lượt là: a) Đ ; b) S.
B. Phép tính khi đổi tên đơn vị 1500m2=…ha là:
0,0001ha×1500=0,15ha
Vậy kết quả lần lượt là: a) S ; b) Đ.
Câu 3.
Phương pháp:
Biểu thức có phép nhân và phép cộng thì ta thực hiện phép nhân trước, thực hiện phép cộng sau.
Cách giải:
25+2,18×5
=25+10,90
=35,9
Vậy kết quả lần lượt là: a) S; b) S; c) Đ.
Câu 4.
Phương pháp:
– Tính số lít dầu hỏa có trong 24 chai == số lít dầu hỏa có trong 1 chai ×24.
– Tính cân nặng của lượng dầu hỏa có trong 24 chai = cân nặng của 1 lít dầu hỏa × số lít dầu hỏa có trong 24 chai.
– Tính cân nặng của 24 vỏ chai = cân nặng của 1 vỏ chai ×24.
– Tính cân nặng của 24 chai đựng đầy dầu hỏa = cân nặng của lượng dầu hỏa có trong 24 chai + cân nặng của 24 vỏ chai.
Cách giải:
Số lít dầu hỏa trong 24 chai là:
0,75×24=18 (lít)
18 lít dầu hỏa nặng số ki-lô-gam là :
0,76×18=13,68(kg)
24 vỏ chai nặng số ki-lô-gam là:
0,25×24=6(kg)
24 chai dầu hỏa nặng số ki-lô-gam là :
13,68+6=19,68(kg)
Đáp số: 19,68kg.
Lưu ý: Có thể tính cân nặng của 1 chai đầy dầu hỏa bằng cách tính tổng cân nặng của 0,75 lít dầu hỏa và cân nặng của 1 vỏ chai. Sau đó để tính cân nặng của 24 chai đựng đầy dầu hỏa ta lấy cân nặng của 1 chai đầy dầu hỏa nhân với 24.
Chọn B.
Câu 5.
Phương pháp:
– Áp dụng tính chất giao hoán và kết hợp của phép nhân để nhóm các số có tích là số tự nhiên lại với nhau.
– Áp dụng tính chất nhân một số với một tổng hoặc nhân một số với một hiệu:
a×(b+c)=a×b+a×c ; a×(b−c)=a×b−a×c



Câu 7.
Phương pháp:
– Vẽ sơ đồ biểu diễn số ki-lô-mét đi được trong mỗi giờ.
– Dựa vào sơ đồ để tìm số ki-lô-mét trung bình mỗi giờ đi được.
– Tính độ dài quãng đường AB ta lấy số ki-lô-mét trung bình mỗi giờ đi được nhân với thời gian ô tô đi hết quãng đường AB.
Cách giải:

Đề số 27 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ, sai ghi S:



Lời giải
Câu 1.
Phương pháp:
Muốn chia một số thập phân với một số tự nhiên ta làm như sau:
– Chia phần nguyên của số bị chia cho số chia.
– Viết dấu phẩy vào bên phải thương đã tìm trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia để tiếp tục thực hiện phép chia.
– Tiếp tục chia với từng chữ số ở phần thập phân của số bị chia.
Cách giải:
Ta đặt tính và thực hiện tính như sau:

Vậy kết quả lần lượt là: S; Đ; S; Đ.
Câu 2.
Phương pháp:
*) Muốn chia một số thập phân với một số tự nhiên ta làm như sau:
– Chia phần nguyên của số bị chia cho số chia.
– Viết dấu phẩy vào bên phải thương đã tìm trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia để tiếp tục thực hiện phép chia.
– Tiếp tục chia với từng chữ số ở phần thập phân của số bị chia.
*) Lưu ý: Để tìm số dư ta dóng thẳng cột dấu phẩy ở số bị chia xuống vị trí của số dư để tìm số dư của phép chia.
Cách giải:
Ta đặt tính và thực hiện tính như sau:

Chọn C.
Câu 3.
Phương pháp:
Khi chia một số tự nhiên cho một số tự nhiên mà còn dư, ta tiếp tục chia như sau:
– Viết dấu phẩy vào bên phải số thương.
– Viết thêm vào bên phải số dư một chữ số 0 rồi chia tiếp.
– Nếu còn dư nữa, ta lại viết thêm bên phải số dư mới một chữ số 0 rồi tiếp tục chia, và có thể cứ làm như thế mãi.
Cách giải:
Ta đặt tính và thực hiện tính như sau:
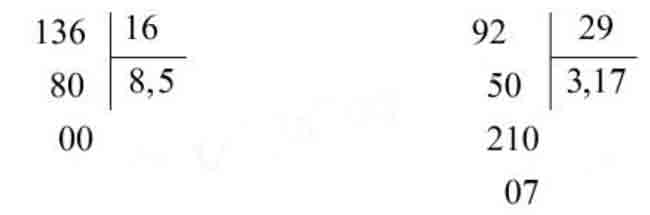
Vậy kết quả lần lượt là:
a) S ; Đ. b) Đ ; S.
Câu 4.
Phương pháp:
Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
Cách giải:

Vậy kết quả lần lượt là: a) S; b) Đ; c) S.
Câu 5.
Phương pháp:
– Tính số tấn hàng 1 ô tô chở được ta lấy số tấn hàng 25 ô tô chở được chia cho 25.
– Tính số tấn hàng 15 ô tô chở được ta lấy số tấn hàng 1 ô tô chở được nhân với 15
Cách giải:
1 ô tô chở được số tấn hàng là:

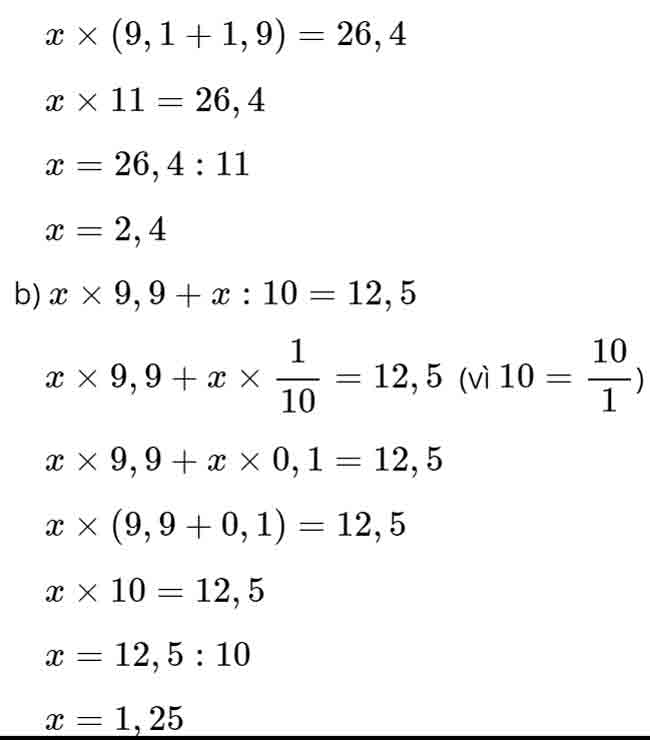




Đề số 28 – Đề kiểm tra học kì 1 – Toán lớp 5




Lời giải
Câu 1.
Phương pháp:
*) Muốn chia một số thập phân với một số tự nhiên ta làm như sau:
– Chia phần nguyên của số bị chia cho số chia.
– Viết dấu phẩy vào bên phải thương đã tìm trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia để tiếp tục thực hiện phép chia.
– Tiếp tục chia với từng chữ số ở phần thập phân của số bị chia.
*) Lưu ý: Để tìm số dư ta dóng thẳng cột dấu phẩy ở số bị chia xuống vị trí của số dư để tìm số dư của phép chia.
Cách giải:
Ta đặt tính và thực hiện tính như sau:
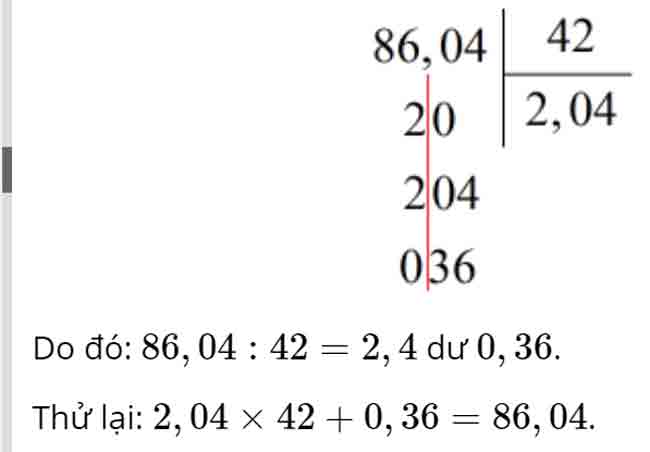
Vậy ta có kết quả như sau: A. S; B. S; C. S; D. Đ.
Câu 2.
Phương pháp:


Câu 4.
Phương pháp:
Tính giá trị hai biểu thức rồi so sánh kết quả với nhau.
Cách giải:

Ta có kết quả lần lượt như sau:
a) S; b) S; c) Đ;
d) S; e) Đ; g) S.
Câu 5.
Phương pháp:
Áp dụng tính chất chia một tổng hoặc một hiệu cho một số:

Câu 6.
Phương pháp:
– Viết phép chia hai số dưới dạng phép nhân hai số.
– Áp dụng tính chất nhân một số với một hiệu:






Đề số 29 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Khoanh vào chữ đặt trước câu trả lời đúng:




Lời giải
Câu 1.
Phương pháp:
Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đổi.
Cách giải:
Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đổi.
Do đó ta có: 8,64:2,4=(8,64×10):(2,4×10)
Chọn B.
Câu 2.
Phương pháp:
Muốn chia một số tự nhiên cho một số thập phân ta làm như sau:
– Đếm xem có bao nhiêu số thập phân ở phần thập phân của số chia thì viết thêm vào bên phải số bị chia bấy nhiêu chữ số 0.
– Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia các số tự nhiên.
Cách giải:
Ta đặt tính và thực hiện tính như sau:

Vậy ta có kết quả như sau: a) S; b) S; c) S; d) Đ.
Câu 3.
Phương pháp:
Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đổi.
Cách giải:
Khi nhân số bị chia và số chia với cùng một số khác 00 thì thương không thay đổi.





Câu 8.
Phương pháp:
– Để tính độ dài đường chéo thứ hai ta lấy 22 lần diện tích chia cho độ dài đường chéo thứ nhất.
– Tính cạnh khu đất ta lấy độ dài đường chéo thứ hai nhân


Đề số 30 – Đề kiểm tra học kì 1 – Toán lớp 5
Đề bài
Câu 1. Nối hai phép tính có kết quả bằng nhau:



được 54km. Một tàu chợ đi từ C đến B dài 180,5km, mỗi giờ đi được 30km. Hai tàu xuất phát cùng một lúc. Hỏi sau bao lâu hai tàu cùng cách B một khoảng cách bằng nhau?Lời giải
Câu 1.
Phương pháp:
Viết số thập phân dưới dạng phân số rồi viết phép chia hai số dưới dạng phép nhân hai số.
Cách giải:
Ta có:


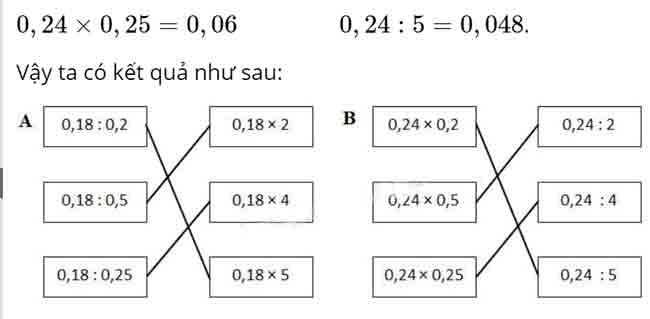
Câu 4.
Phương pháp:
Viết phần phân số của hỗn số dưới dạng phân số thập phân, sau đó viết hỗn số dưới dạng số thập phân.
Cách giải:




Câu 8.
Phương pháp:
Hai tàu đã cho chuyển động cùng chiều về phía B và xuất phát cùng lúc. Lúc hai tàu cùng cách B một khoảng cách bằng nhau thì lúc đó hai tàu gặp nhau tại một địa điểm D nào đó (D nằm giữa A và B). Để giải bài này ta có thể làm như sau:
– Tìm hiệu độ dài quãng đường từ A đến B và quãng đường từ C đến B.
– Tìm số ki-lô-mét tàu nhanh đi nhiều hơn tàu chợ trong 1 giờ.
– Tìm thời gian để hai tàu cùng cách B một khoảng cách bằng nhau (tức thời gian đi để hai tàu gặp nhau kể từ lúc xuất phát) ta lấy hiệu độ dài quãng đường từ A đến B và quãng đường từ C đến B chia cho số ki-lô-mét tàu nhanh đi nhiều hơn tàu chợ trong 1 giờ.
Cách giải:
Quãng đường từ A đến B dài hơn quãng đường từ C đến B một đoạn là:

Mọi chi tiết liên hệ với chúng tôi :TRUNG TÂM GIA SƯ TÂM TÀI ĐỨCCác số điện thoại tư vấn cho Phụ Huynh :Điện Thoại : 091 62 65 673 hoặc 01634 136 810Các số điện thoại tư vấn cho Gia sư :Điện thoại : 0902 968 024 hoặc 0908 290 601
Từ khóa » Tích Của 19 2 Và 0 78 Là
-
1. Hiện Nay Mẹ Hơn Con 24 Tuổi Và Tuổi Con Bằng 13 Tuổi Mẹ. Hỏi ...
-
Tích Của Hai Số Tự Nhiên Bằng 78. Tìm Mỗi SốGIÚP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
-
B. Hoạt động Thực Hành - Bài 24 : So Sánh Hai Số Thập Phân
-
Lý Thuyết: Sử Dụng Máy Tính Bỏ Túi để Hỗ Trợ Giải Toán Về Số Phần Trăm
-
Giải Toán Lớp 5 VNEN: So Sánh Hai Số Thập Phân
-
Đề Thi Học Kì 2 Toán Lớp 5 Nâng Cao Năm 2021 - 2022 Có đáp án (5 đề)
-
Sách Giải Bài Tập Toán Lớp 7 Bài 10: Làm Tròn Số
-
Giải Sách Bài Tập Toán 7 Bài 10: Làm Tròn Số
-
VONG 10 TOAN VIOLYMPIC LOP 5 NAM HOC 20162017 - 123doc
-
Thông Tư 78 Và Quy định Về Hóa đơn điện Tử PHẢI BIẾT 2022