Định Lí đảo Và Hệ Quả Của định Lí Ta-lét - Chuyên đề Môn Toán Lớp 8
Có thể bạn quan tâm
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ ZaloĐịnh lí đảo và hệ quả của định lí Ta-lét là nội dung được học trong chương trình Toán 8 học kì 2. Để giúp các em nắm vững kiến thức được học trong bài, VnDoc gửi tới các bạn Chuyên đề Toán học lớp 8: Định lí đảo và hệ quả của định lí Ta-lét. Hy vọng tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hơn. Mời các bạn tham khảo.
Chuyên đề: Định lí đảo và hệ quả của định lí Ta-lét
- A. Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét
- B. Trắc nghiệm & Tự luận Định lí đảo và hệ quả của định lí Ta-lét
A. Lý thuyết Định lí đảo và hệ quả của định lí Ta-lét
1. Định lý đảo
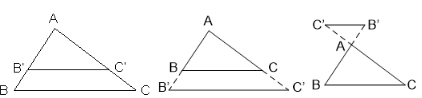
Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
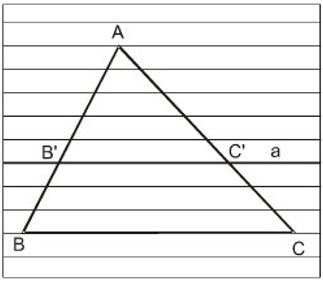
Tổng quát: Δ ABC, B' ∈ AB, C' ∈ AC; AB'/BB' = AC'/C'C
Suy ra: B'C'//BC.
Ví dụ: Trong Δ ABC có AB = 6cm, AC = 9cm. Lấy trên cạnh AB điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 2cm, AC' = 3cm. Chứng minh B'C'//BC.
Hướng dẫn:
Trong Δ ABC, B' ∈ AB, C' ∈ AC.
Ta có
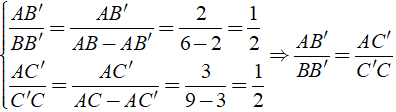
Suy ra: B'C'//BC.
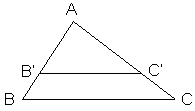
2. Hệ quả của định lý Ta – lét
Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
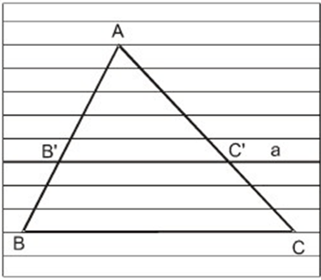
Tổng quát : Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
Ta có: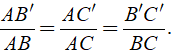
Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.
Ví dụ: Trong Δ ABC có AB = 8cm và B'C'//BC. Lấy trên cạnh AB điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 2cm, AC' = 3cm. Tính độ dài cạnh AC.
Hướng dẫn:
Áp dụng hệ quả trên ta có: Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
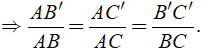
Khi đó ta có: AB'/AB = AC'/AC ⇔ 2/8 = 3/AC ⇒ AC = (3.8)/2 = 12( cm )
B. Trắc nghiệm & Tự luận Định lí đảo và hệ quả của định lí Ta-lét
I. Bài tập trắc nghiệm
Bài 1: Tính x trong trường hợp sau:
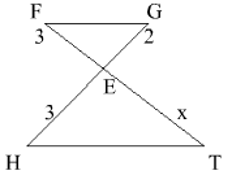
A. x = 4,5
B. x = 3
C. x = 2
D. Cả 3 đáp án trên đều sai
Áp dụng hệ quả của định lí Ta – lét với FG//HT ta có:
FG//HT ⇒ EF/ET = EG/HE ⇔ ET = (EF.HE)/EG = (3.3)/2 = 4,5
Chọn đáp án A.
Bài 2: Cho hình bên. Chọn câu trả lời đúng?
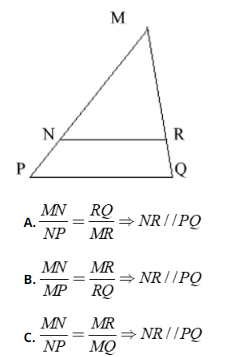
D. Cả 3 đáp án đều sai.
Ta có:
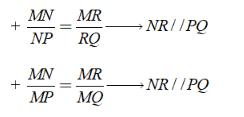
Cả 3 đáp án A, B, C đều sai.
Chọn đáp án D.
Bài 3: Cho hình bên. Chọn câu trả lời đúng?
A. SL/LK = HI/HK ⇒ SH//LI
B. SL/SK = HI/HK ⇒ SH//LI
C. HI/HK = LK/SL ⇒ SH//LI
D. HK/HI = SL/SK ⇒ SH//LI
Ta có:
+ SL/LK = HI/IK → SH//LI
+ SL/SK = HI/HK → SH//LI
Chọn đáp án B.
Bài 4: Cho Δ ABC có độ dài các cạnh như hình vẽ Kết quả nào sau đây đúng?
A. ED/BC = 1,5
B. ED/BC = 3/7,5
C. ED/BC = 3/5
D. Cả 3 đáp án đều sai.
Ta có: ED//BC ⇒ ED/BC = AE/AB = AD/AC = 3/5
Chọn đáp án C.
Bài 5: Cho tam giác ABC có trọng tâm G.A', B', C' là trung điểm của BC, CA , AB. Phát biểu nào sau đây sai.
A.GA và GN tỉ lệ với GA' và GB'
B. GA và GA' tỉ lệ với AC và B'C
C. GB' và GC' tỉ lệ với GB và GA
D. Đường cao AH của tam giác ABC và đường cao GD của tam giác GBC tỉ lệ với AA'và GA'.
Chọn đáp án D
Bài 6: Cho M và N là hai điểm lần lượt thuộc hai cạnh AB và AC của tam giác ABC. Biết MN=6cm, AM=3cm, MB=5cm, AC=16cm, Cn=10cm. Độ dài của cạnh là:
A. BC=10cm
B. BC=9cm
C. BC=16cm
D. Một kết quả khác
Chọn đáp án A
Bài 7: Cho tam giác ABC, M và N là hai điểm lần lượt thuộc cạnh AB, AC. Biết AM=2cm, MB=5cm, AN=3,2cm, NC=8cm, BC=14cm. Độ dài đoạn thẳng MN là:
A. MN=5,6cm
B. MN=4cm
C. MN=8cm
D. MN=5,2cm
Chọn đáp án D
Bài 8: Tính x trong hình vẽ bên
A. x=4,5
B. x=3
C. x=2
D. Cả 3 câu trên đều sai
Chọn đáp án C.
Bài 9: Cho hình thang ABCD (AB // CD) có diện tích 36cm2, AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
A. 8cm2
B. 6cm2
C. 16cm2
D. 32cm2
Chọn đáp án C.
Bài 10: Cho hình thang ABCD (AB // CD) có diện tích 48cm2 , AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
A. 64 /3 cm2
B. 15cm2
C. 16cm2
D. 32cm2
Chọn đáp án A
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Tính độ dài x, y trong các hình bên
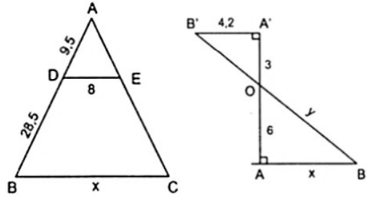
Hướng dẫn:
a) Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = (8.28,5)/9,5 = 456/19 ≈ 31,58
b) Ta có: A'B'//AB vì cùng vuông góc AA'
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'//AB ⇒ AB/A'B' = AO/A'O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
OB2 = AB2 + OA2 ⇒ y = √(8,42 + 62) ≈ 10,32
Bài 2: Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
Hướng dẫn:
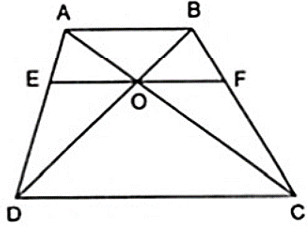
Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
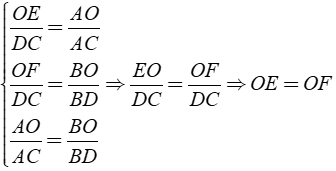
Điều phải chứng minh.
........................
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Định lí đảo và hệ quả của định lí Ta-lét. Hy vọng thông qua tài liệu này, các em học sinh sẽ nắm vững kiến thức được học về Định lí đảo và hệ quả của định lí Ta-lét, từ đó vận dụng làm các bài tập liên quan hiệu quả.
Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
Từ khóa » Bài Tập Về định Lý Talet Thuận
-
[CHUẨN NHẤT] Bài Tập Về định Lý Talet Lớp 8 Có đáp án - TopLoigiai
-
15 Bài Tập Định Lí Ta-lét Trong Tam Giác Có đáp án | Toán Lớp 8
-
Chuyên đề định Lí Ta-lét Trong Tam Giác - Toán THCS
-
Định Lý Talet Thuận, định Lý Talet đảo Và Hệ Quả Của định Lý Talet
-
Định Lý Talet Là Gì? Bài Tập định Lý Talet Có Lời Giải Chi Tiết - Icongchuc
-
[Top Bình Chọn] - Bài Tập Về định Lý Talet - Trần Gia Hưng
-
Định Lý Talet Nội Dung Căn Bản Và Bài Tập Vận Dụng
-
Bài Tập định Lý Ta-lét. Định Lý đảo Và Hệ Quả Của định Lý Ta-lét Toán 8 ...
-
Định Lý Talet Và Những Hệ Quả Của định Lý Talet | Wikikienthuc
-
Toán 8: Định Lý Talet Trong Tam Giác, Trong Hình Thang
-
Phát Biểu định Lí Talet Thuận, đảo. Giả Thiết, Kết Luận, Vẽ Hình Câu 2
-
34 Câu Trắc Nghiệm Định Lý Ta - Lét Có đáp án - Toán Lớp 8
-
Các Dạng Bài Tập Về Định Lí Ta-lét Trong Tam Giác Chọn Lọc