Định Lí Pi-ta-go Và Cách Giải Các Dạng Bài Tập | Toán Lớp 7

Định lí Pi-ta-go và cách giải các dạng bài tập - Toán lớp 7

I. LÝ THUYẾT:

1. Định lí Pytago:

Trong tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

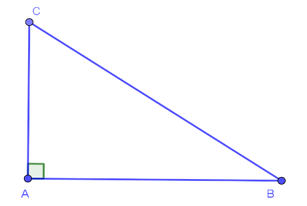
∆ABC vuông tại A: BC2 = AB2 + AC2

2. Định lí Pytago đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

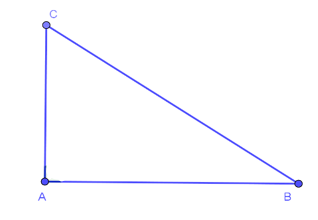
∆ABC có BC2 = AB2 + AC2 thì ∆ABC vuông tại A

II. CÁC DẠNG BÀI TẬP CƠ BẢN:

Dạng 4.1: Tính độ dài một cạnh của tam giác vuông khi biết độ dài hai cạnh.

1. Phương pháp giải:

- Sử dụng định lí Py- ta-go trong tam giác vuông

∆ABC vuông tại A: BC2 = AB2 + AC2

- Có trường hợp phải kẻ thêm đường vuông góc để tạo thành tam giác vuông.

2. Ví dụ minh họa:

Ví dụ 1: Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC (H nằm giữa A và C). Tính độ dài BC, biết HA = 1cm, HC = 8cm.

Giải:

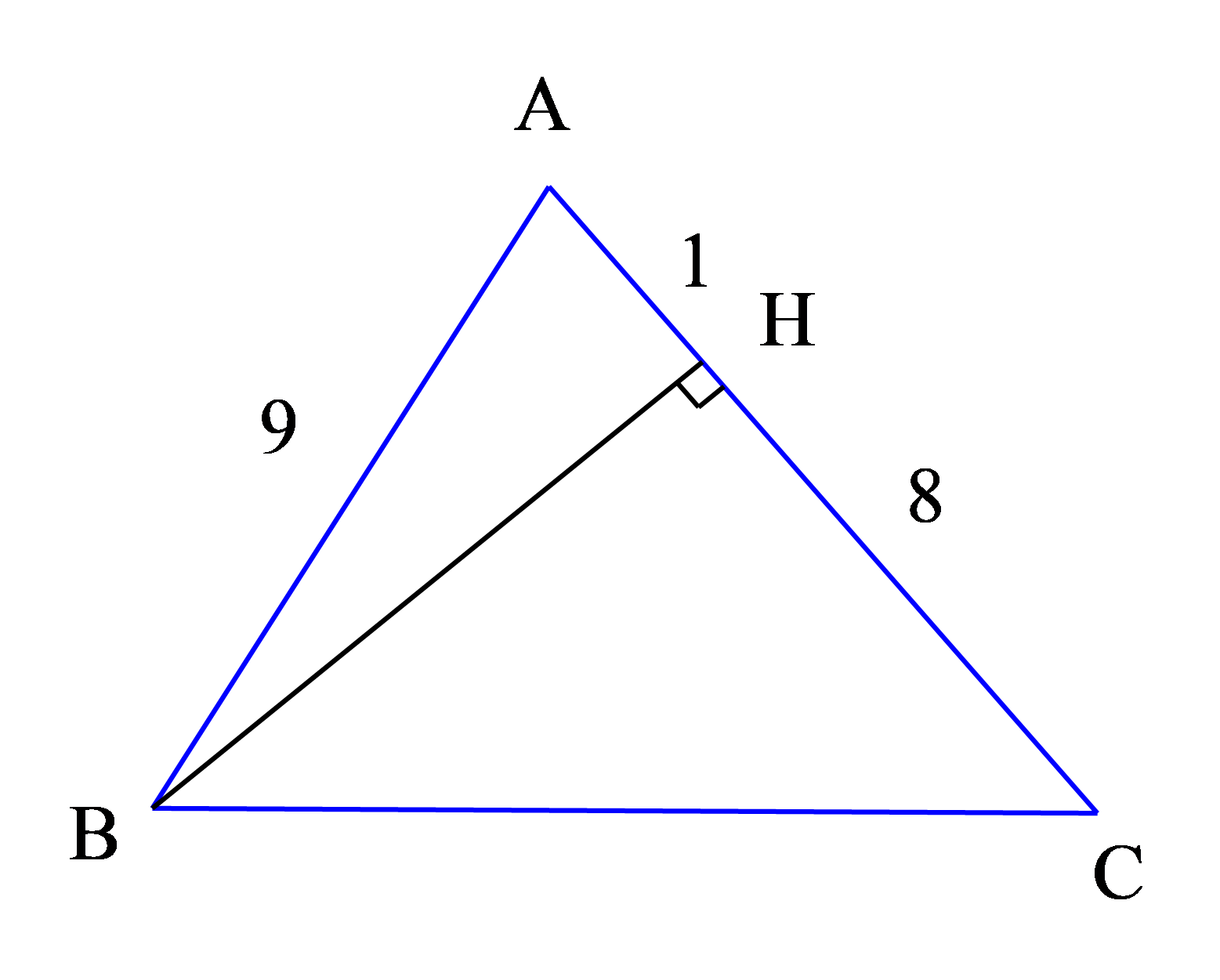
GT	ΔABC,  AB=AC BH⊥AC (H nằm giữa A và C) HA = 1cm, HC = 8cm
KL	BC = ?

Ta có AC = AH + HC = 1 + 8 = 9 cm

Lại có ∆ABC cân tại A nên AB = AC = 9 cm

Áp dụng định lí Py-ta-go cho Δ ABH vuông tại H ta có:

AB2 = AH2 + BH2 ⇒ BH2 = AB2 – AH2 = 92 – 12 = 80

Áp dụng định lí Py-ta-go cho Δ BCHvuông tại H ta có:

BC2 = BH2 + CH2 = 80 + 82 = 144

⇒ BC = 12

Vậy độ dài BC = 12 cm.

Ví dụ 2: Cho∆ABC vuông ở A có ABAC  =  815, BC = 51. Tính AB, AC.

Giải:

Áp dụng định lý Py – ta – go cho ΔABC vuông tại A có: BC2=AB2+AC2

Có ABAC=815⇒AB8=AC15

⇒AB264=AC2225=AB2+AC264+225=BC2289=512289=9

⇒AB8=AC15=3

Suy ra: AB = 8 . 3 = 24; AC = 15 . 8 = 45

Vậy AB = 24; AC = 45.

Dạng 4.2: Sử dụng định lý Py - ta - go để nhận biết tam giác vuông.

1. Phương pháp giải:

- Tính bình phương các độ dài ba cạnh của tam giác.

- So sánh bình phương của cạnh lớn nhất với tổng các bình phương của hai cạnh kia.

- Nếu hai kết quả bằng nhau thì tam giác đó là tam giác vuông, cạnh lớn nhất là cạnh huyền.

2. Ví dụ minh họa:

Ví dụ 3: Cho tam giác ABC có AB = 8 cm, AC = 6 cm, BC = 10 cm. Hỏi tam giác ABC là tam giác gì?

Giải:

Ta có 62 =36, 82 = 64, 102 = 100

Mà 100 = 36 + 64 hay 102 = 82 + 62

Nên theo định lí Py - ta - go đảo, tam giác ABC là tam giác vuông tại A.

III. BÀI TẬP VẬN DỤNG:

Bài 1: Độ dài một cạnh góc vuông của một tam giác vuông cân bằng 3 cm. Độ dài cạnh huyền bằng?

A. 6 cm

B.12  cm

C. 18  cm

D. 3,5 cm

Bài 2: Ba số nào dưới đây có thể là độ dài ba cạnh của một tam giác vuông?

A. 4cm; 5cm; 6cm

B. 6cm; 6cm; 9cm

C. 5cm; 13cm;15cm

D. 20cm; 21cm; 29cm

Bài 3: Tam giác có độ dài ba cạnh bằng 4cm, 7cm, 8cm có là tam giác vuông không? Vì sao?

Bài 4: Cho tam giác ABC vuông tại A, ABAC=34. Biết BC = 20cm, tính các độ dài AB, AC.

Bài 5: Tính diện tích của tam giác ABC. Biết rằng AB = 12cm, AC = 16cm, BC = 20cm.

Bài 6: Cho tam giác ABC. Kẻ AH vuông góc BC (H nằm giữa B và C). Biết

BH = 9cm, HC = 16cm, HA = 12cm. Chứng minh tam giác ABC vuông tại A.

Bài 7: Cho các độ dài 6cm, 7cm, 8cm, 10cm, 24cm, 26cm. Ba độ dài nào có thể là độ dài các cạnh của tam giác vuông?

Bài 8: Tam giác ABC có góc A^ tù, C^=30o,  AB=29,  AC=40. Vẽ đường cao AH và tính BH.

Bài 9: Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC (H nằm giữa A và C). Biết HA = 7cm, HC = 18cm. Tính các độ dài BH và BC.

Bài 10: Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD.

Chứng minh rằng:

a) BE = CD

b)   ΔBMD=ΔCME

c) AM là phân giác của BAC^.

Hướng dẫn giải:

Bài 1: Đáp án C.

Bài 2: Đáp án D.

Bài 3: Ta có 42 =16, 72 = 49, 82 = 64

Mà 16 + 49 = 65 ≠ 64

Nên theo định lí Py - ta - go đảo, tam giác có độ dài 3 cạnh 4m, 7m, 8m không là tam giác vuông.

Bài 4: Đặt AB = 3k, AC = 4k

Theo định lý Py-ta-go ta có:

AB2 + AC2 = BC2

⇒ (3k)2 + (4k)2 = 202

⇒ k = 4

Vậy AB =12cm; AC = 16cm.

Bài 5: Áp dụng định lý Py-ta-go đảo, ta biết được tam giác ABC vuông tại A.

SABC=12AB.AC=12.12.16=96cm2

Bài 6:

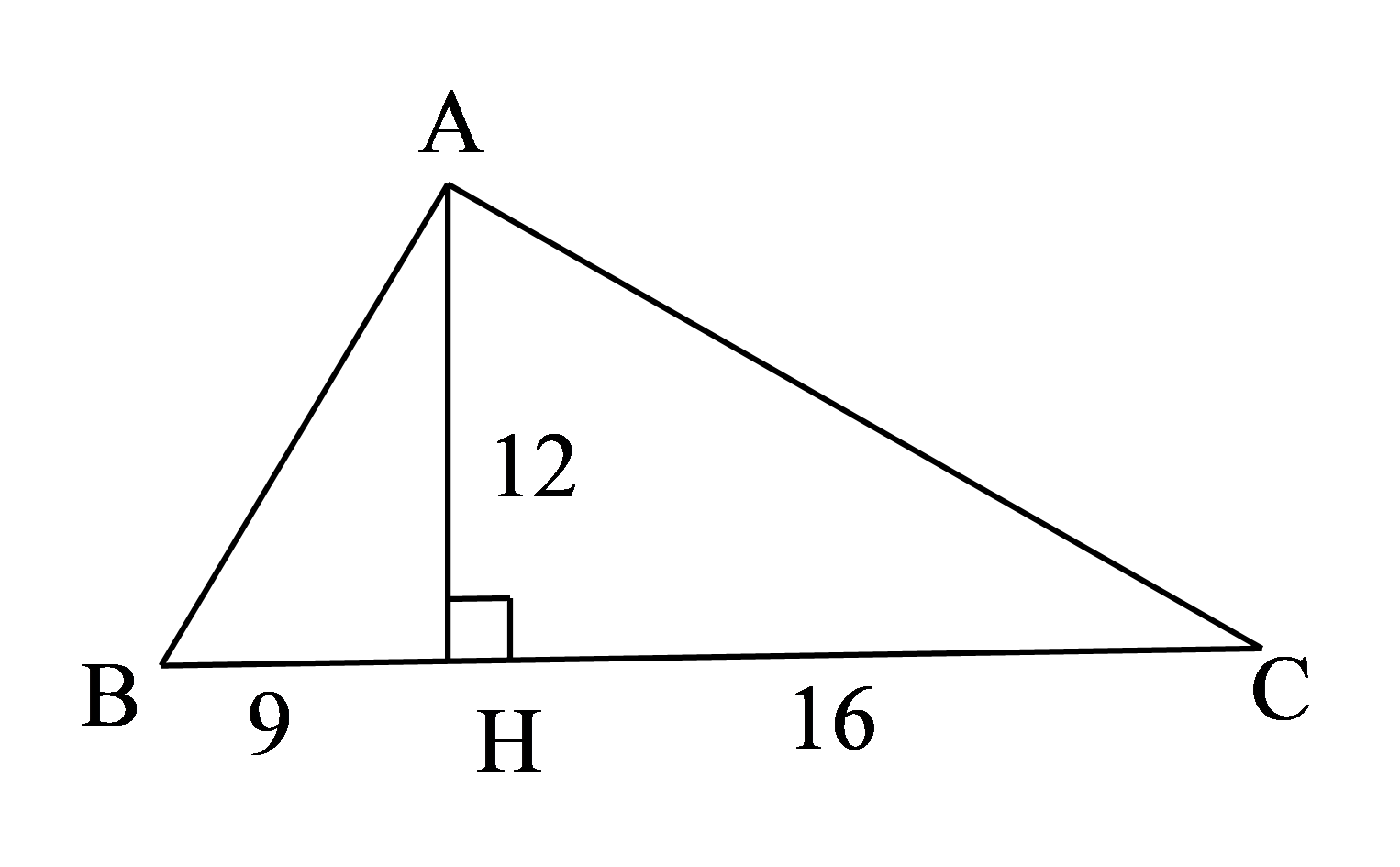
+) Áp dụng Py-ta-go cho hai tam giác vuông ABH và ACH được:

AB = 15; AC = 20

+) BC = 25

BC2 = AB2 + AC2 (252 = 152 + 202).

Theo định lý Py-ta-go đảo, tam giác ABC vuông tại A.

Bài 7: Ba độ dài độ dài các cạnh của tam giác vuông là (6; 8; 10), (10; 24; 26).

Bài 8:

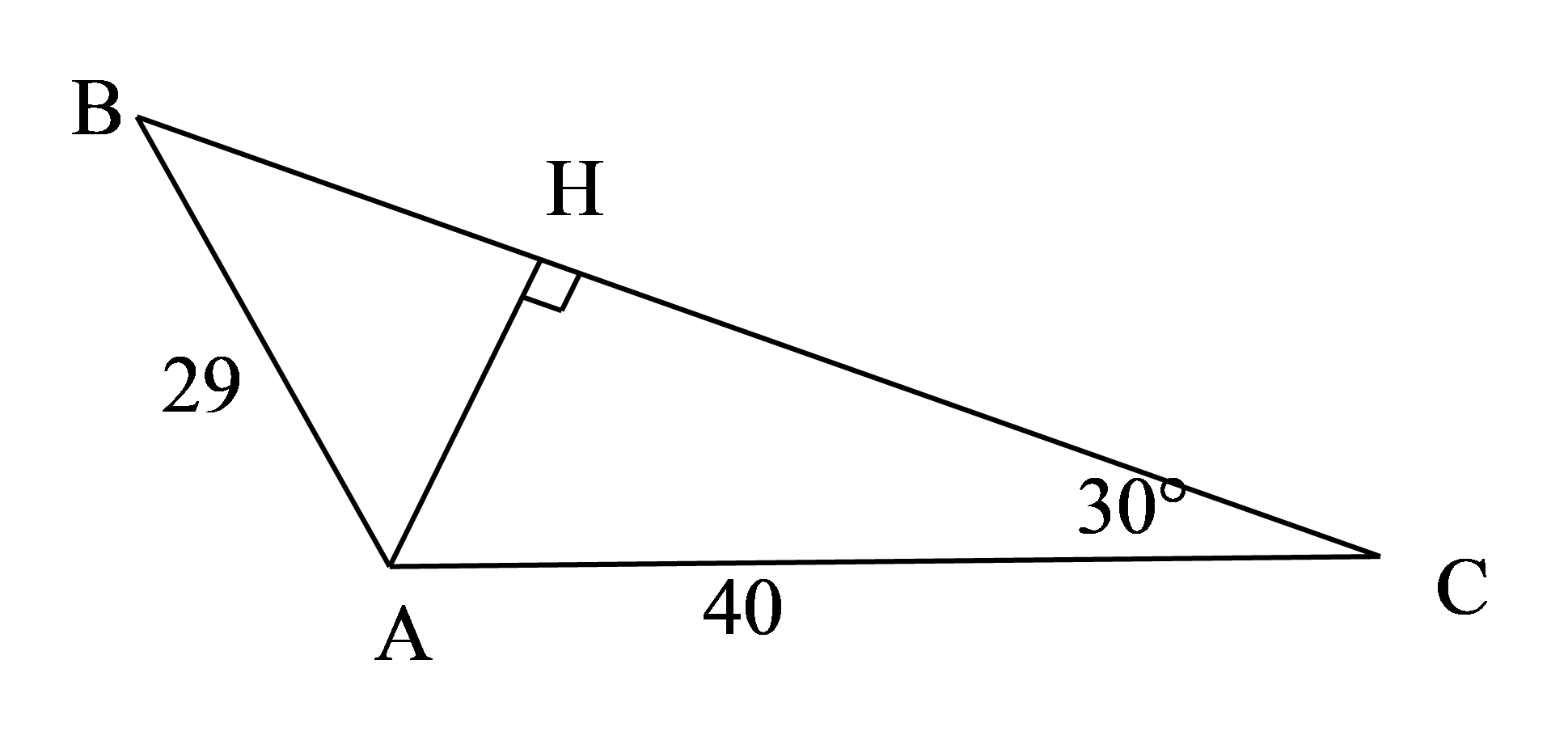
Xét ΔAHC vuông ở H có C^=30o nên AH = 12AC  = 20

Áp dụng định lý Py-ta-go vào tam giác vuông ABH ta được BH = 21.

Bài 9:

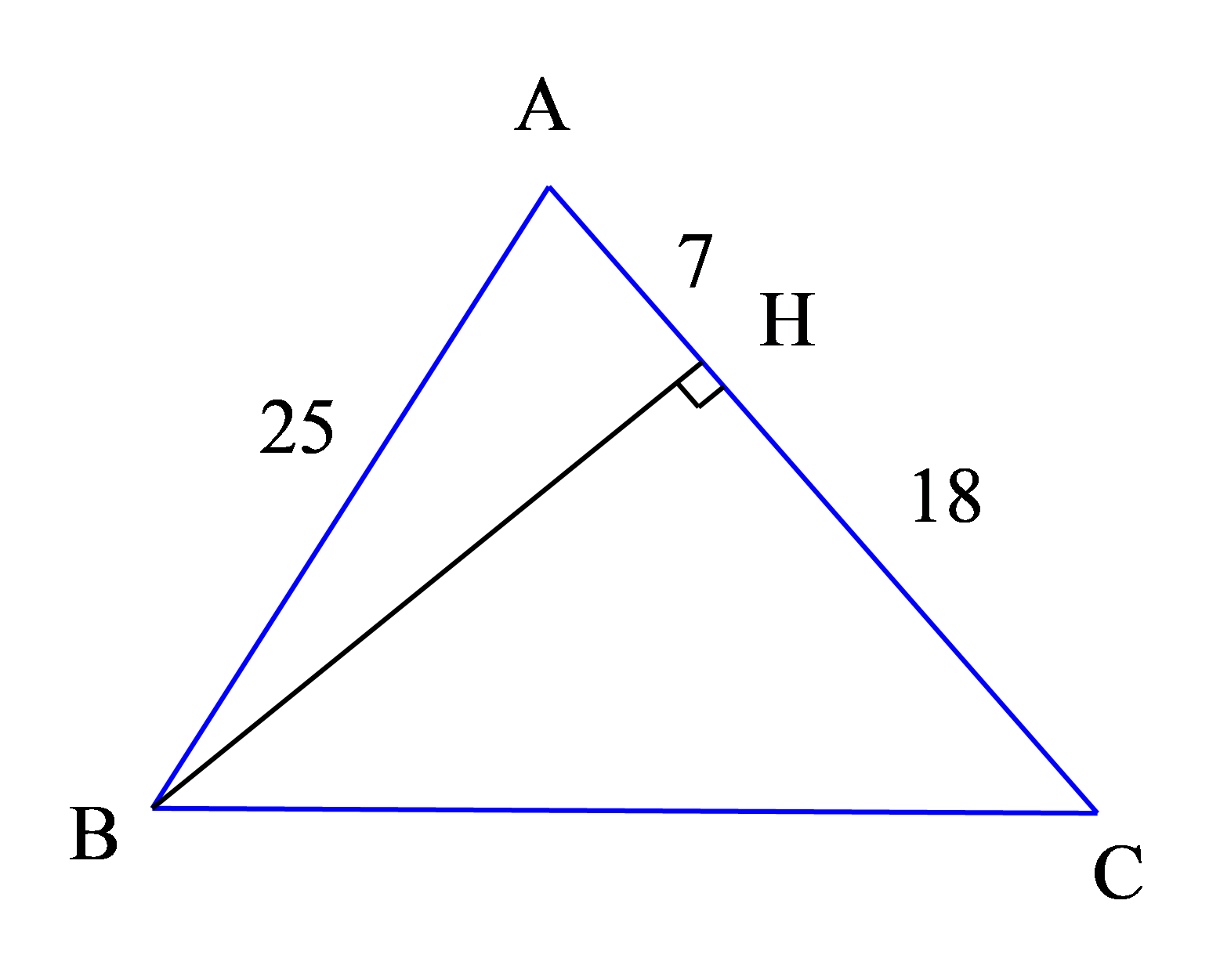Tam giác ABC cân tại A nên:

AB = AC = HA + HC = 7 + 18 = 25cm

Áp dụng định lý Py-ta-go vào tam giác AHB vuông tại H ta có: BH = 24cm

Áp dụng Py-ta-go vào tam giác vuông BHC được BC = 30cm.

Bài 10:

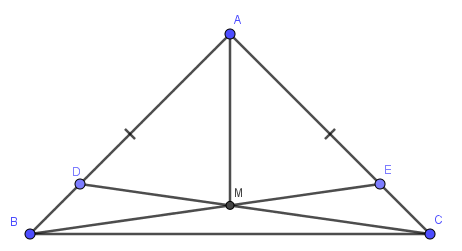
a)   ΔABE=ΔACD  (c.g.c) suy ra BE = CD

b) Ta có ΔMDB=ΔMEC  (g.c.g)

Do đó: MB = MC

c)ΔAMB=ΔAMC  (c.c.c)

Suy ra: MAB^=MAC^. Hay AM là phân giác của góc BAC.

Xem thêm các dạng bài tập Toán lớp 7 có đáp án và lời giải chi tiết khác:

Tổng ba góc của một tam giác và cách giải các dạng bài tập

Hai tam giác bằng nhau và các trường hợp bằng nhau của hai tam giác – Toán lớp 7

Tam giác cân, Tam giác đều và cách giải các dạng bài tập

Các trường hợp bằng nhau của hai tam giác vuông và cách giải