ĐỊNH LÍ TA-LÉT TRONG TAM GIÁC - Học Để Thi
Có thể bạn quan tâm

- Trang Chủ
- Giáo Trình
- Giáo Trình Toán
- Giáo Trình Hóa
- Ðề Thi Ðại Học
- Toán Học
- Hóa Học
- Vật Lý
- Sinh Học
- Môn Van
- Ðịa Lý
- Lịch Sử
- Tất Cả Ðề Thi Và Ðáp Án
- Ôn Thi Ðại Học
- Tài Liệu Toán Học
- Tài Liệu Hóa Học
- Video Hóa Học
- Tài Liệu Vật Lý
- Sinh Học
- Môn Van
- Ðịa Lý
- Lịch Sử
- Tất Cả Tài Liệu Ôn Thi
- Ðề Thi TN-THPT
- Giải Nhanh Hóa
- Ðặt Câu Hỏi
- Đặt câu hỏi 2
- Trắc Nghiệm
- Vật Lý
- Hóa Học
- Sinh Học
- English
ĐỊNH LÍ TA-LÉT TRONG TAM GIÁC
§. ĐỊNH LÍ TA-LÉT TRONG TAM GIÁC A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ I. Tỉ số của hai đoạn thẳng Định nghĩa : Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo. II. Đoạn thẳng tỉ lệ Định nghĩa : Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức : 
 III. Định lí Ta-lét trong tam giác Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ. IV. Định lí Ta-lét đảo
III. Định lí Ta-lét trong tam giác Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ. IV. Định lí Ta-lét đảo  Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. Cho tam giác ABC (h.4)
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. Cho tam giác ABC (h.4)  Þ a // BC II. Hệ quả của định lí Ta-lét
Þ a // BC II. Hệ quả của định lí Ta-lét  Nếu một đường thẳng cắt hai cạnh (hoặc cắt phần kéo dài của hai cạnh) của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho. Cho tam giác ABC : a // BC Þ
Nếu một đường thẳng cắt hai cạnh (hoặc cắt phần kéo dài của hai cạnh) của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho. Cho tam giác ABC : a // BC Þ  . (h.5) B/ BÀI TẬP 1. Cho góc xAy khác góc bẹt. Trên tia Ax lấy các điểm B, C. Qua B và C vẽ hai đường thẳng song song cắt Ay lần lượt ở D và E. Qua E vẽ đường thẳng song song với CD cắt tia Ax ở F. a) So sánh
. (h.5) B/ BÀI TẬP 1. Cho góc xAy khác góc bẹt. Trên tia Ax lấy các điểm B, C. Qua B và C vẽ hai đường thẳng song song cắt Ay lần lượt ở D và E. Qua E vẽ đường thẳng song song với CD cắt tia Ax ở F. a) So sánh  và
và  ;
;  b) Chứng minh rằng: AC2 = AB.AF 2. Cho G là trọng tâm tam giác ABC. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh rằng : BD =
b) Chứng minh rằng: AC2 = AB.AF 2. Cho G là trọng tâm tam giác ABC. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh rằng : BD =  . 3. Đường thẳng d cắt các cạnh AB, AD và đường chéo AC của hình bình hành ABCD lần lượt tại E, F và O. Chứng minh rằng
. 3. Đường thẳng d cắt các cạnh AB, AD và đường chéo AC của hình bình hành ABCD lần lượt tại E, F và O. Chứng minh rằng  . 4. Cho tam giác ABC có AM là đường trung tuyến. N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chứng minh rằng
. 4. Cho tam giác ABC có AM là đường trung tuyến. N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chứng minh rằng  . 5. Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BO, AO. Lấy điểm F trên cạnh AB sao cho tia FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: a)
. 5. Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BO, AO. Lấy điểm F trên cạnh AB sao cho tia FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: a)  b) BE + AK ³ BC. 6. Cho tam giác vuông cân ABC có góc C = 900 .Từ C kẻ một tia vuông góc với trung tuyến AM cắt AB ở D. Hãy tính tỉ số
b) BE + AK ³ BC. 6. Cho tam giác vuông cân ABC có góc C = 900 .Từ C kẻ một tia vuông góc với trung tuyến AM cắt AB ở D. Hãy tính tỉ số  . 7. Cho điểm E thuộc cạnh AC của DABC . Qua B kẻ một đường thẳng I.Đường thẳng qua E và song song với BC cắt I tại N. Đường thẳng qua E và song song với AB cắt I tại M. Chứng minh rằng AN // CM. 8. Cho hình thang ABCD có BC // AD. Trên AC kéo dài lấy 1 điểm P tùy ý . Đường thẳng qua P và trung điểm của BC cắt AB tại M và đường thẳng qua P và trung điểm của AD cắt CD tại N. Chứng minh rằng MN // AD. 9. Tứ giác ABCD có M, N lần lượt là trung điểm của các đường chéo AC và BD. Gọi G là trọng tâm D ABC. Nối GC cắt MN tại O . Chứng minh rằng : OC = 3 OG 10. Cho hình thang ABCD ( AB // CD ) với AB = a ; CD = b. Gọi I là giao điểm của hai đường chéo . Đường thẳng qua I và song song với AB cắt hai cạnh bên tại E và F. Chứng minh rằng :
. 7. Cho điểm E thuộc cạnh AC của DABC . Qua B kẻ một đường thẳng I.Đường thẳng qua E và song song với BC cắt I tại N. Đường thẳng qua E và song song với AB cắt I tại M. Chứng minh rằng AN // CM. 8. Cho hình thang ABCD có BC // AD. Trên AC kéo dài lấy 1 điểm P tùy ý . Đường thẳng qua P và trung điểm của BC cắt AB tại M và đường thẳng qua P và trung điểm của AD cắt CD tại N. Chứng minh rằng MN // AD. 9. Tứ giác ABCD có M, N lần lượt là trung điểm của các đường chéo AC và BD. Gọi G là trọng tâm D ABC. Nối GC cắt MN tại O . Chứng minh rằng : OC = 3 OG 10. Cho hình thang ABCD ( AB // CD ) với AB = a ; CD = b. Gọi I là giao điểm của hai đường chéo . Đường thẳng qua I và song song với AB cắt hai cạnh bên tại E và F. Chứng minh rằng :  11. Hình bình hành ABCD. Gọi M là một điểm trên đường chéo AC. Vẽ ME vuông góc với AB và MF vuông góc với AD. Chứng minh rằng :
11. Hình bình hành ABCD. Gọi M là một điểm trên đường chéo AC. Vẽ ME vuông góc với AB và MF vuông góc với AD. Chứng minh rằng : 12. Hình thang ABCD đáy lớn CD. Qua A vẽ đường thẳng AK // BC cắt BD tại E. Qua B vẽ đường thẳng BI // AD cắt AC tại F ( K ; I thuộc CD). Chứng minh rằng: a)EF // AB b)AB2 = CD . EF. 13. Cho 1 điểm M nằm trong D ABC. Đường thẳng qua M và trọng tâm G của tam giác cắt BC; CA và AB theo thứ tự D, E, F. Chứng minh rằng
12. Hình thang ABCD đáy lớn CD. Qua A vẽ đường thẳng AK // BC cắt BD tại E. Qua B vẽ đường thẳng BI // AD cắt AC tại F ( K ; I thuộc CD). Chứng minh rằng: a)EF // AB b)AB2 = CD . EF. 13. Cho 1 điểm M nằm trong D ABC. Đường thẳng qua M và trọng tâm G của tam giác cắt BC; CA và AB theo thứ tự D, E, F. Chứng minh rằng  14. Cho D ABC cân tại A. Hai điểm D và E theo thứ tự thay đổi trên AB và BC. Kẻ DF vuông góc với BC. Chứng minh rằng nếu
14. Cho D ABC cân tại A. Hai điểm D và E theo thứ tự thay đổi trên AB và BC. Kẻ DF vuông góc với BC. Chứng minh rằng nếu  thì đường thẳng qua E và vuông góc với DE luôn đi qua I điểm cố định. 15. Cho tam giác ABC, trọng tâm G, đường thẳng ( d) qua G cắt các cạnh AB và AC tại M và N. Chứng minh rằng : AM. AN = AM. NC + AN . MB. 16. Cho tam giác ABC vuông tại A. Giả sử đường cao AH, trung tuyến BM, và phân giác trong CN đồng quy. Chứng minh rằng BH = AC. 17. Cho tam giác ABC, AM, BN và CP cắt nhau tại I. Tìm I để:
thì đường thẳng qua E và vuông góc với DE luôn đi qua I điểm cố định. 15. Cho tam giác ABC, trọng tâm G, đường thẳng ( d) qua G cắt các cạnh AB và AC tại M và N. Chứng minh rằng : AM. AN = AM. NC + AN . MB. 16. Cho tam giác ABC vuông tại A. Giả sử đường cao AH, trung tuyến BM, và phân giác trong CN đồng quy. Chứng minh rằng BH = AC. 17. Cho tam giác ABC, AM, BN và CP cắt nhau tại I. Tìm I để:  nhỏ nhất. 18. Cho tứ giác ABCD. Đường thẳng qua A song song với BC cắt BD tại P và đường thẳng qua B song song với AD cắt AC ở Q. Chứng minh rằng PQ // CD. 19. Lấy một điểm O trong tam giác ABC, các tia AO, BO, CO cắt BC, AC, AB lần lượt tại P, Q, R. Chứng minh rằng
nhỏ nhất. 18. Cho tứ giác ABCD. Đường thẳng qua A song song với BC cắt BD tại P và đường thẳng qua B song song với AD cắt AC ở Q. Chứng minh rằng PQ // CD. 19. Lấy một điểm O trong tam giác ABC, các tia AO, BO, CO cắt BC, AC, AB lần lượt tại P, Q, R. Chứng minh rằng  . 20. Cho A¢, B¢, C¢ lần lượt nằm trên cạnh BC, AC, AB của tam giác ABC. Biết rằng AA¢, BB¢, CC¢ đồng quy tại M. Chứng minh rằng :
. 20. Cho A¢, B¢, C¢ lần lượt nằm trên cạnh BC, AC, AB của tam giác ABC. Biết rằng AA¢, BB¢, CC¢ đồng quy tại M. Chứng minh rằng :  . 21. Cho một điểm M ở trong góc xOy. Một đường thẳng d qua M cắt 2 cạnh của góc ở A và B . Chứng minh rằng tổng
. 21. Cho một điểm M ở trong góc xOy. Một đường thẳng d qua M cắt 2 cạnh của góc ở A và B . Chứng minh rằng tổng  không phụ thuộc vị trí của d. 22. Cho hình bình hành ABCD . Một đường thẳng bất kỳ qua A cắt BD, CD và BC lần lượt tại E, F và G. Chứng minh rằng :
không phụ thuộc vị trí của d. 22. Cho hình bình hành ABCD . Một đường thẳng bất kỳ qua A cắt BD, CD và BC lần lượt tại E, F và G. Chứng minh rằng : . 23. Cho tam giác ABC và trung tuyến AD. Một đường thẳng bất kỳ song song với AD cắt BC, CA, AB lần lượt tại E, N, M . Chứng minh rằng:
. 23. Cho tam giác ABC và trung tuyến AD. Một đường thẳng bất kỳ song song với AD cắt BC, CA, AB lần lượt tại E, N, M . Chứng minh rằng:  24. DABC ( AB < AC ) có trung tuyến AM; phân giác AD. Đường thẳng qua M và song song với AD cắt AB tại E và AC tại F . Chứng minh : a) DAEF cân b) AC – AB = 2 AE. §.TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ I. Định lí : Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
24. DABC ( AB < AC ) có trung tuyến AM; phân giác AD. Đường thẳng qua M và song song với AD cắt AB tại E và AC tại F . Chứng minh : a) DAEF cân b) AC – AB = 2 AE. §.TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC A/ KIẾN THỨC VÀ KĨ NĂNG CẦN NHỚ I. Định lí : Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.  AD là phân giác góc BAC Þ
AD là phân giác góc BAC Þ  II. Chú ý Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.
II. Chú ý Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.  AE¢ là tia phân giác góc BAx (AB ¹ AC) Þ
AE¢ là tia phân giác góc BAx (AB ¹ AC) Þ  (h.9) B/ BÀI TẬP 1. Cho
(h.9) B/ BÀI TẬP 1. Cho  ABC, AD là đường phân giác. Chứng minh :
ABC, AD là đường phân giác. Chứng minh :  . 2. Tam giác ABC vuông tại A có AB = 8 cm, BC = 10 cm và có AD là đường phân giác. Tính các đoạn DB, DC. 3. Cho tam giác ABC và AD, BE, CF là ba đường phân giác. Chứng minh rằng
. 2. Tam giác ABC vuông tại A có AB = 8 cm, BC = 10 cm và có AD là đường phân giác. Tính các đoạn DB, DC. 3. Cho tam giác ABC và AD, BE, CF là ba đường phân giác. Chứng minh rằng  = 1. 4. Cho tam giác ABC, AM là đường trung tuyến. Các đường phân giác của góc BMA và góc CMA cắt AB và AC tương ứng tại D và E. Chứng minh rằng DE // BC. 5. Cho tam giác ABC. O là giao điểm các đường phân giác ta đặt AB = c, AC = b, BC = a. AO cắt BC tại D. Tính DB,
= 1. 4. Cho tam giác ABC, AM là đường trung tuyến. Các đường phân giác của góc BMA và góc CMA cắt AB và AC tương ứng tại D và E. Chứng minh rằng DE // BC. 5. Cho tam giác ABC. O là giao điểm các đường phân giác ta đặt AB = c, AC = b, BC = a. AO cắt BC tại D. Tính DB,  theo a, b, c. 6. Cho tam giác ABC cân tại A, (AB = AC = m, BC = n),
theo a, b, c. 6. Cho tam giác ABC cân tại A, (AB = AC = m, BC = n),  = 360. Chứng minh rằng n2 + m.n – m2 = 0 7. Chứng minh rằng tam giác ABC là tam giác vuông nếu các đường phân giác BD, CE cắt nhau tại I thoả mãn:
= 360. Chứng minh rằng n2 + m.n – m2 = 0 7. Chứng minh rằng tam giác ABC là tam giác vuông nếu các đường phân giác BD, CE cắt nhau tại I thoả mãn:  . 8. Cho 3 tia Ox, Oy, Oz tạo thành
. 8. Cho 3 tia Ox, Oy, Oz tạo thành  chứng minh rằng nếu A, B, C là 3 điểm thẳng hàng trên Ox, Oy, Oz thì ta có
chứng minh rằng nếu A, B, C là 3 điểm thẳng hàng trên Ox, Oy, Oz thì ta có  9. Gọi da , db , dc là độ dài các đường phân giác thuộc các cạnh a, b, c của tam giác ABC.Chứng minh
9. Gọi da , db , dc là độ dài các đường phân giác thuộc các cạnh a, b, c của tam giác ABC.Chứng minh  10. Gọi b và c là độ dài các cạnh AC,AB của tam giác ABC,da là độ dài phân giác thuộc cạnh BC. Chứng minh rằng điều kiện cần và đủ để tam giác ABC có
10. Gọi b và c là độ dài các cạnh AC,AB của tam giác ABC,da là độ dài phân giác thuộc cạnh BC. Chứng minh rằng điều kiện cần và đủ để tam giác ABC có  là
là  11. Cho
11. Cho  ABC trung tuyến BM cắt phn gic CD của
ABC trung tuyến BM cắt phn gic CD của  tại P. Chứng minh :
tại P. Chứng minh :  12. Cho
12. Cho  ABC vuơng tại A(AB < AC), kẻ đường cao AH, trung tuyến AM. Đường thẳng vuơng gĩc với AM tại A cắt đường thẳng BC tại D. Chứng minh rằng : a) AB l tia phngic gĩc DAH b) BH. CD = BD. CH 13. Cho
ABC vuơng tại A(AB < AC), kẻ đường cao AH, trung tuyến AM. Đường thẳng vuơng gĩc với AM tại A cắt đường thẳng BC tại D. Chứng minh rằng : a) AB l tia phngic gĩc DAH b) BH. CD = BD. CH 13. Cho  ABC, các tia phân giác trong BM, CN (M
ABC, các tia phân giác trong BM, CN (M AC, N
AC, N AB) cắt nhau tại D. Chứng minh rằng :
AB) cắt nhau tại D. Chứng minh rằng :  ABC vuơng tại A
ABC vuơng tại A 2BD. CD = BM. CN 14. Cho
2BD. CD = BM. CN 14. Cho  ABC, có AD, BE, CF theo thứ tự là các đường phân giác trong của góc A, B, C. Gọi I và K theo thứ tự là các điểm đối xứng với A qua các đường thẳng BE, CF, G và H theo thứ tự là các điểm đối xứng với B và C qua đường thẳng AD. Chứng minh rằng: GI//HK. §. KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT I. KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG 1. Tam giác đồng dạng a) Định nghĩa Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:
ABC, có AD, BE, CF theo thứ tự là các đường phân giác trong của góc A, B, C. Gọi I và K theo thứ tự là các điểm đối xứng với A qua các đường thẳng BE, CF, G và H theo thứ tự là các điểm đối xứng với B và C qua đường thẳng AD. Chứng minh rằng: GI//HK. §. KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT I. KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG 1. Tam giác đồng dạng a) Định nghĩa Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:  ;
;  ;
;  ;
;  =
=  =
=  Tam giác A'B'C' đồng dạng với tam giác ABC được kí hiệu làDA'B'C' ∽DABC (viết theo thứ tự cặp đỉnh tương ứng). Tỉ số các cạnh tương ứng
Tam giác A'B'C' đồng dạng với tam giác ABC được kí hiệu làDA'B'C' ∽DABC (viết theo thứ tự cặp đỉnh tương ứng). Tỉ số các cạnh tương ứng  =
=  =
=  = k gọi là tỉ số đồng dạng. b) Tính chất Tính chất 1. Mỗi tam giác đồng dạng với chính nó Tính chất 2. Nếu DA'B'C' ∽DABC thì DABC ∽DA'B'C'
= k gọi là tỉ số đồng dạng. b) Tính chất Tính chất 1. Mỗi tam giác đồng dạng với chính nó Tính chất 2. Nếu DA'B'C' ∽DABC thì DABC ∽DA'B'C'  Tính chất 3. Nếu DA'B'C' ∽DA''B''C" và DA''B''C" ∽DABC thìD A'B'C' ∽DABC. 2. Định lí Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho. Cho DABC. MN // BC ÞDAMN ∽DABC (h.12) Chú ý Định lí cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài hai cạnh của tam giác và song với cạnh còn lại. II. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT Định lí : Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng. DABC và DA¢B¢C¢ có
Tính chất 3. Nếu DA'B'C' ∽DA''B''C" và DA''B''C" ∽DABC thìD A'B'C' ∽DABC. 2. Định lí Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho. Cho DABC. MN // BC ÞDAMN ∽DABC (h.12) Chú ý Định lí cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài hai cạnh của tam giác và song với cạnh còn lại. II. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT Định lí : Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng. DABC và DA¢B¢C¢ có 
 ÞDABC ∽DA¢B¢C¢ (c.c.c) BÀI TẬP 1. Cho DABC ∽DA¢B¢C¢. Chứng tỏ rằng
ÞDABC ∽DA¢B¢C¢ (c.c.c) BÀI TẬP 1. Cho DABC ∽DA¢B¢C¢. Chứng tỏ rằng 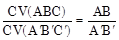 (với CV là chu vi tam giác). 2. Cho tam giác ABC, vẽ tam giác A¢B¢C¢ đồng dạng với tam giác ABC theo tỉ số đồng dạng k =
(với CV là chu vi tam giác). 2. Cho tam giác ABC, vẽ tam giác A¢B¢C¢ đồng dạng với tam giác ABC theo tỉ số đồng dạng k =  . 3. Cho hai tam giác MNP và RSK có MN = 9 cm, MP = 12 cm,NP = 15cm, RS = 5cm, KR = 3cm, KS = 4cm. Chứng minh rằng
. 3. Cho hai tam giác MNP và RSK có MN = 9 cm, MP = 12 cm,NP = 15cm, RS = 5cm, KR = 3cm, KS = 4cm. Chứng minh rằng  4. Cho hai tam giác ABC và DEF có : AB = 48cm, AC = 20cm,BC = 52cm, DE = 6cm, DF = 2,5cm, AC = 5cm, BC = 13cm,
4. Cho hai tam giác ABC và DEF có : AB = 48cm, AC = 20cm,BC = 52cm, DE = 6cm, DF = 2,5cm, AC = 5cm, BC = 13cm, = 900. Chứng minh rằng
= 900. Chứng minh rằng  5. Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Chứng minh rằng DOAB∽DOCD. 6. a) Cho tam giác ABC. Các điểm D, E, F lần lượt là trung điểm các cạnh AB, BC, AC. Chứng minh rằng DEFD ∽DABC b) Cho M là điểm tuỳ ý trong tam giác ABC. Gọi A¢, B¢, C¢ lần lượt là trọng tâm của các tam giác MBC, MCA, MAB. Chứng minh rằng DABC ∽DA¢B¢C¢. 7. Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh rằng DEAK ∽DECH. 8. Cho tam giác ABC có BC = a, AC = b, AB = c và a2 = bc. Chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC. 9. Cho tứ giác ABCD có AB = 1,5cm, BC = 2,5cm, CD = 6cm,AD = 5cm, AC = 3cm. Chứng minh rằng tứ giác ABCD là hình thang. 10. Cho
5. Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Chứng minh rằng DOAB∽DOCD. 6. a) Cho tam giác ABC. Các điểm D, E, F lần lượt là trung điểm các cạnh AB, BC, AC. Chứng minh rằng DEFD ∽DABC b) Cho M là điểm tuỳ ý trong tam giác ABC. Gọi A¢, B¢, C¢ lần lượt là trọng tâm của các tam giác MBC, MCA, MAB. Chứng minh rằng DABC ∽DA¢B¢C¢. 7. Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh rằng DEAK ∽DECH. 8. Cho tam giác ABC có BC = a, AC = b, AB = c và a2 = bc. Chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC. 9. Cho tứ giác ABCD có AB = 1,5cm, BC = 2,5cm, CD = 6cm,AD = 5cm, AC = 3cm. Chứng minh rằng tứ giác ABCD là hình thang. 10. Cho  ABC có AB = 4cm, AC = 6cm, BC = 9cm. Gọi h1, h2, h3 là chiều cao tương ứng với các cạnh BC, AC, AB. Chứng minh rằng
ABC có AB = 4cm, AC = 6cm, BC = 9cm. Gọi h1, h2, h3 là chiều cao tương ứng với các cạnh BC, AC, AB. Chứng minh rằng  ABC đồng dạng với tam giác có ba cạnh bằng h1, h2, h3. 11. Cho tứ giác ABCD có AB = 8cm,BC = 4cm, CD = 20cm, AD = 25cm, AC = 10cm. Chứng minh tứ giác ABCD là hình thang.
ABC đồng dạng với tam giác có ba cạnh bằng h1, h2, h3. 11. Cho tứ giác ABCD có AB = 8cm,BC = 4cm, CD = 20cm, AD = 25cm, AC = 10cm. Chứng minh tứ giác ABCD là hình thang.
14 comments:
 UnknownJanuary 22, 2015 at 2:41 PM
UnknownJanuary 22, 2015 at 2:41 PMtoàn là bài tập gì đâu ko...
ReplyDeleteReplies- Reply
 UnknownAugust 5, 2015 at 3:30 PM
UnknownAugust 5, 2015 at 3:30 PMHay. Thanks ad
ReplyDeleteReplies- Reply
 UnknownFebruary 16, 2016 at 3:41 PM
UnknownFebruary 16, 2016 at 3:41 PMadd ơi, mình bị lỗi gì đó, k xem đc hình. add có thể share cho mình tài liệu này đc không? thank
ReplyDeleteReplies- Reply
 vu inh nguDecember 21, 2016 at 11:28 AM
vu inh nguDecember 21, 2016 at 11:28 AMdit mem may nhu loz
ReplyDeleteReplies An Vy NguyễnJanuary 26, 2018 at 9:42 PM
An Vy NguyễnJanuary 26, 2018 at 9:42 PMtrẻ trâu z
DeleteReplies- Reply
Reply
 UnknownJune 21, 2017 at 8:11 AM
UnknownJune 21, 2017 at 8:11 AMđề trên đây khá tốt
ReplyDeleteReplies- Reply
 AnonymousAugust 4, 2017 at 11:42 AM
AnonymousAugust 4, 2017 at 11:42 AMNgay trong phần 1 định lý thì đã có chỗ không chuẩn rồi. "AB và CD tỷ lệ..." Điểm D là điểm nào vậy?
ReplyDeleteReplies UnknownSeptember 12, 2017 at 10:19 PM
UnknownSeptember 12, 2017 at 10:19 PMLÀ 2 ĐOẠN THẲNG MÀ AB VÀ CD, A'B' VÀ C'D'
DeleteReplies- Reply
 UnknownSeptember 12, 2017 at 10:20 PM
UnknownSeptember 12, 2017 at 10:20 PMBẠN NÊN XEM KỸ LẠI NHA KHÔNG PHẢI THEO CÁI HÌNH ĐÂU
DeleteReplies- Reply
Reply
 UnknownNovember 7, 2018 at 8:46 PM
UnknownNovember 7, 2018 at 8:46 PMcó mấy bạn trẻ trâu zậy? haiz
ReplyDeleteReplies- Reply
 UnknownDecember 18, 2018 at 11:02 PM
UnknownDecember 18, 2018 at 11:02 PMcó đáp án k ad
ReplyDeleteReplies- Reply
 Blue SkyMarch 19, 2019 at 9:09 PM
Blue SkyMarch 19, 2019 at 9:09 PMDell có giải à
ReplyDeleteReplies- Reply
 dat triApril 4, 2019 at 9:45 PM
dat triApril 4, 2019 at 9:45 PMcó đáp án ko ạ
ReplyDeleteReplies- Reply
 UnknownDecember 15, 2019 at 6:53 PM
UnknownDecember 15, 2019 at 6:53 PMcho mình hỏi nếu như tam giác lòng với nhau thì dùng talet như thế nào ?
ReplyDeleteReplies- Reply
 Trang Trước Trang Tiếp Theo
Trang Trước Trang Tiếp TheoBài Ðược Xem Nhiều
- Đặt Câu Hỏi Hiện trang đặt câu hỏi năm 2013 và năm 2012 đều bị lổi không sử dụng được nữa, Thầy sẽ liên hệ google để được giải quyết. Do đó, nếu có câu...
- Đặt Câu Hỏi Nếu các em, bạn có những bài khó không giải được, hoặc có thắt mắt gì muốn được giải đáp thì có thể đặt câu hỏi bênh dưới rồi comments lại,...
-
Tìm m để phương trình có 4 nghiệm Tìm m để Phương trình: x 4 -2x 2 -m=0 có 4 nghiệm phân biệt. Đặt t=x 2 =>t>=0 Phương trình trở thành: t 2 -2t-m=0 (*) ...
-
 NHỮNG HẰNG ĐẲNG THỨC ĐÁNG NHỚ B . NHỮNG HẰNG ĐẲNG THỨC ĐÁNG NHỚ 1. (A+B) 2 = A 2 +2AB+B 2 2. (A – B) 2 = A 2 – 2AB+ B 2 3. A 2 – B 2 = (A-B)(A+B) 4. (A+B) 3 = A 3 +3A 2...
NHỮNG HẰNG ĐẲNG THỨC ĐÁNG NHỚ B . NHỮNG HẰNG ĐẲNG THỨC ĐÁNG NHỚ 1. (A+B) 2 = A 2 +2AB+B 2 2. (A – B) 2 = A 2 – 2AB+ B 2 3. A 2 – B 2 = (A-B)(A+B) 4. (A+B) 3 = A 3 +3A 2... -
 PHƯƠNG PHÁP CHUẨN ĐỘ AXIT – BAZƠ PHƯƠNG PHÁP CHUẨN ĐỘ AXIT – BAZƠ I. Đặc điểm. - Dùng phương pháp này để xác định nồng độ axit, bazơ. - ...
PHƯƠNG PHÁP CHUẨN ĐỘ AXIT – BAZƠ PHƯƠNG PHÁP CHUẨN ĐỘ AXIT – BAZƠ I. Đặc điểm. - Dùng phương pháp này để xác định nồng độ axit, bazơ. - ... -
 Every New Apple Product Known or Rumored for 2025: A Deep Dive into What’s Coming January 2025 feels like it's lasted about 27 years, but there's an entire year left, somehow. As usual, Apple is sure to make the ...
Every New Apple Product Known or Rumored for 2025: A Deep Dive into What’s Coming January 2025 feels like it's lasted about 27 years, but there's an entire year left, somehow. As usual, Apple is sure to make the ... - Công Thức Giải Nhanh Hóa Học Download: Công thức giải nhanh hóa học
-
 AI Tự Động Định Hình Xu Hướng Công Nghệ Năm Nay: Rò Rỉ Tính Năng AI Của Samsung Galaxy S25 Trước Thềm Sự Kiện Unpacked 2025 AI tự động tiếp tục định hình xu hướng đổi mới công nghệ trong năm nay, khi một rò rỉ mới đã tiết lộ rằng Samsung Galaxy S25 đáng mong chờ...
AI Tự Động Định Hình Xu Hướng Công Nghệ Năm Nay: Rò Rỉ Tính Năng AI Của Samsung Galaxy S25 Trước Thềm Sự Kiện Unpacked 2025 AI tự động tiếp tục định hình xu hướng đổi mới công nghệ trong năm nay, khi một rò rỉ mới đã tiết lộ rằng Samsung Galaxy S25 đáng mong chờ... - Số phận thế giới khi Donald Trump làm Tổng thống Số phận thế giới khi Donald Trump làm Tổng thống Khi Donald Trump nhậm chức Tổng thống Hoa Kỳ vào năm 2017, ông mang theo một phong cách l...
-
 Qui hoạch tuyến tính_DQK3091 TRƯỜNG ĐẠI HỌC SÀI GÒN ĐỀ THI KẾT THÚC MÔN HỌC Môn thi: Qui hoạch tuyến tính ...
Qui hoạch tuyến tính_DQK3091 TRƯỜNG ĐẠI HỌC SÀI GÒN ĐỀ THI KẾT THÚC MÔN HỌC Môn thi: Qui hoạch tuyến tính ...
Blog active
- ► 2025 (194)
- ► November (1)
- ► October (6)
- ► May (2)
- ► April (1)
- ► March (32)
- ► February (123)
- ► January (29)
- ► 2024 (6)
- ► May (6)
- ► 2023 (11)
- ► November (1)
- ► May (3)
- ► February (6)
- ► January (1)
- ► 2022 (30)
- ► December (5)
- ► October (1)
- ► September (2)
- ► August (3)
- ► May (1)
- ► April (11)
- ► March (3)
- ► February (1)
- ► January (3)
- ► 2021 (832)
- ► November (307)
- ► October (245)
- ► September (153)
- ► August (115)
- ► July (1)
- ► June (11)
- ► 2020 (81)
- ► December (1)
- ► August (9)
- ► July (25)
- ► June (8)
- ► May (5)
- ► March (2)
- ► February (3)
- ► January (28)
- ► 2019 (40)
- ► April (9)
- ► March (9)
- ► February (22)
- ► 2018 (57)
- ► December (44)
- ► November (13)
- ► 2016 (24)
- ► April (9)
- ► March (15)
- ► 2015 (4)
- ► June (1)
- ► January (3)
- ► 2013 (2986)
- ► December (278)
- ► November (32)
- ► September (118)
- ► August (228)
- ► July (92)
- ► June (370)
- ► May (282)
- ► April (504)
- ► March (416)
- ► February (121)
- ► January (545)
- ► 2012 (349)
- ► December (166)
- ► November (11)
- ► October (39)
- ► September (1)
- ► August (57)
- ► March (74)
- ► February (1)
© 2012 Học Để ThiBlog tài liệu
Từ khóa » định Lý Talet Trong Tam Giác Là Gì
-
Định Lí Ta Lét Trong Tam Giác Và Những Hệ Quả Bạn Cần Biết
-
Lý Thuyết: Định Lí Ta-lét Trong Tam Giác
-
Định Lý Talet Và Talet đảo Trong Tam Giác, Tam Giác Vuông Toán ...
-
Lý Thuyết định Lí TaLet Trong Tam Giác | SGK Toán Lớp 8
-
Tìm Hiểu Về định Nghĩa Và Những Hệ Quả Của định Lý Talet - VOH
-
Định Lý Talet Trong Tam Giác, Tính Chất đường Phân Giác - Abcdonline
-
Định Lý Talet Và Những Hệ Quả Của định Lý Talet
-
Định Lý Talet Và Những Hệ Quả Của định Lý Talet
-
Định Lý Thales – Wikipedia Tiếng Việt
-
Định Lý Ta Lét Là Gì? Những Hệ Quả Của định Lý Talet
-
Định Lý Talet Thuận, định Lý Talet đảo Và Hệ Quả Của định Lý Talet
-
Định Lý Talet Và 3 Hệ Quả Cực Kỳ Quan Trọng Cùng Bài Tập Áp Dụng
-
Định Lý Talet Trong Tam Giác, Trong Hình Thang – Toán Lớp 8
 Unknown
Unknown Anonymous
Anonymous