Định Lý Ptolemy - TaiLieu.VN

Mạng xã hội chia sẻ tài liệu Upload Đăng nhập Nâng cấp VIP Trang chủ » Khoa Học Tự Nhiên » Toán học - Thống kê14 trang 745 lượt xem 550Định lý Ptolemy

Hình học là một trong những lĩnh vực toán học mang lại cho người yêu toán nhiều điều thú vị nhất và khó khăn nhất. Nó đòi hỏi ta phải có những suy nghĩ sáng tạo và tinh tế. Trong lĩnh vực này cũng xuất hiện ko ít những định lí, phương pháp nhằm nâng cao tính hiệu quả trong quá trình giải quyết các bài toán, giúp ta chinh phục những đỉnh núi ngồ ghề và hiểm trở .

Chủ đề:

duongminhthong110395

Tính toán khoa học

Tài liệu Tính toán khoa học

SaveLikeShareReport Download AI tóm tắt /14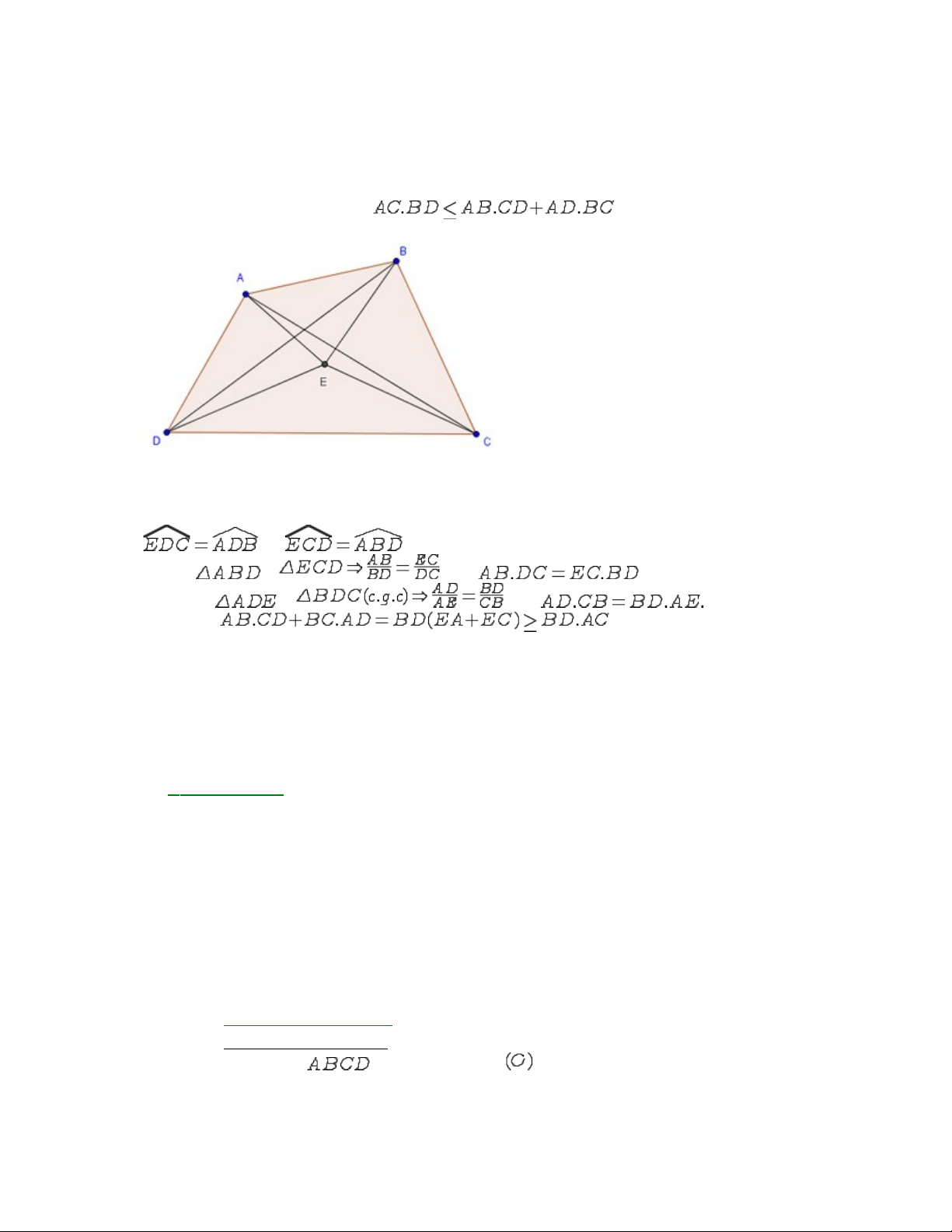I.10) Bt đng thc PtolemyấẳứĐnh lý: ịCho t giác ABCD. Khi đó có ứChng minh: ứLy E nm trong t giác ABCD sao cho ấằứvà Khi đó ~ hay .Hn na ơữ~ hay Vy ta có ậ(đpcm).KHÁM PHÁĐỊNH LÍ PTÔ-LÊ-MÊtác giả:Zai zaiI. Mởđầu: Hình học là một trong những lĩnh vực toán học mang lại cho người yêu toán nhiều điều thú vị nhất và khó khăn nhất. Nóđòi hỏi ta phải có những suy nghĩ sáng tạo vàtinh tế. Trong lĩnh vực này cũng xuất hiện ko ít những định lí, phương pháp nhằm nâng cao tính hiệu quả trong quá trình giải quyết các bài toán, giúp ta chinh phục những đỉnh núi ngồ ghề và hiểm trở . Trong bài viết này zaizai xin giới thiệu đến các bạn một vài điều cơ bản nhất vềđịnh lí Ptô-lê-mê trong việc chứng minh các đặc tính của hình học phẳng. Dùđã rất cố gắng nhưng bài viết sẽ không thể tránh khỏi những thiếu xót mong rằng các bạn sẽ cùng zaizai bổ sung và phát triển nó.II, Nội dung - Lí thuyết:1. Đẳng thức Ptô-lê-mê:Cho tứ giác nội tiếp đường tròn . Khi đó: Hình minh họa (hình 1)Chứng minh:Lấy thuộc đường chéo sao cho Khi đó xét và có: Nên đồng dạng với Do đó ta có:. Lại có: và nên Suy ra hay Từ và suy ra:Vậy đẳng thức Ptô-lê-mêđược chứng minh.2, Bất đẳng thức Ptô-lê-mê:Đây có thể coi làđịnh lí Ptô-mê-lê mở rộng bởi vì nó không giới hạn trong lớp tứ giác nội tiếp .Định lí: Cho tứ giác . Khi đó:Hình minh họa (hình 2) Chứng minh:Trong lấy điểm M sao cho:Dễ dàng chứng minh: Cũng từ kết luận trên suy ra:Áp dụng bất đẳng thức trong tam giác và các điều trên ta có:Vậy định lí Ptô-lê-mê mở rộng đã được chứng minh.3, Định lí Ptô-lê-mê tổng quát: Trong mặt phẳng định hướng cho đa giác nội tiếp đường tròn . M là một điểm thuộc cung (Không chứa )Khi đó:.Trong đó:Đây là một định lí ko dễ dàng chứng minh được bằng kiến thức hình học THCS. Các bạn có thể tham khảo phép chứng minh trong bài viết Định lí Ptô-lê-mê tổng quát của Tiến sĩ Nguyễn Minh Hà, ĐHSP , Hà Nội thuộc Tuyển tập 5 năm Tạp chí toán học và tuổi trẻ. III, Ứng dụng của định lí Ptô-lê-mê trong việc chứng minh các đặc tính hình học:1, Chứng minh quan hệ giữa các đại lượng hình học:Mởđầu cho phần này chúng ta sẽđến với 1 ví dụ điển hình và cơ bản về việc ứng dụng định lí Ptô-lê-mê.Bài toán 1: Cho tam giác đều có các cạnh bằng Trên lấy điểm 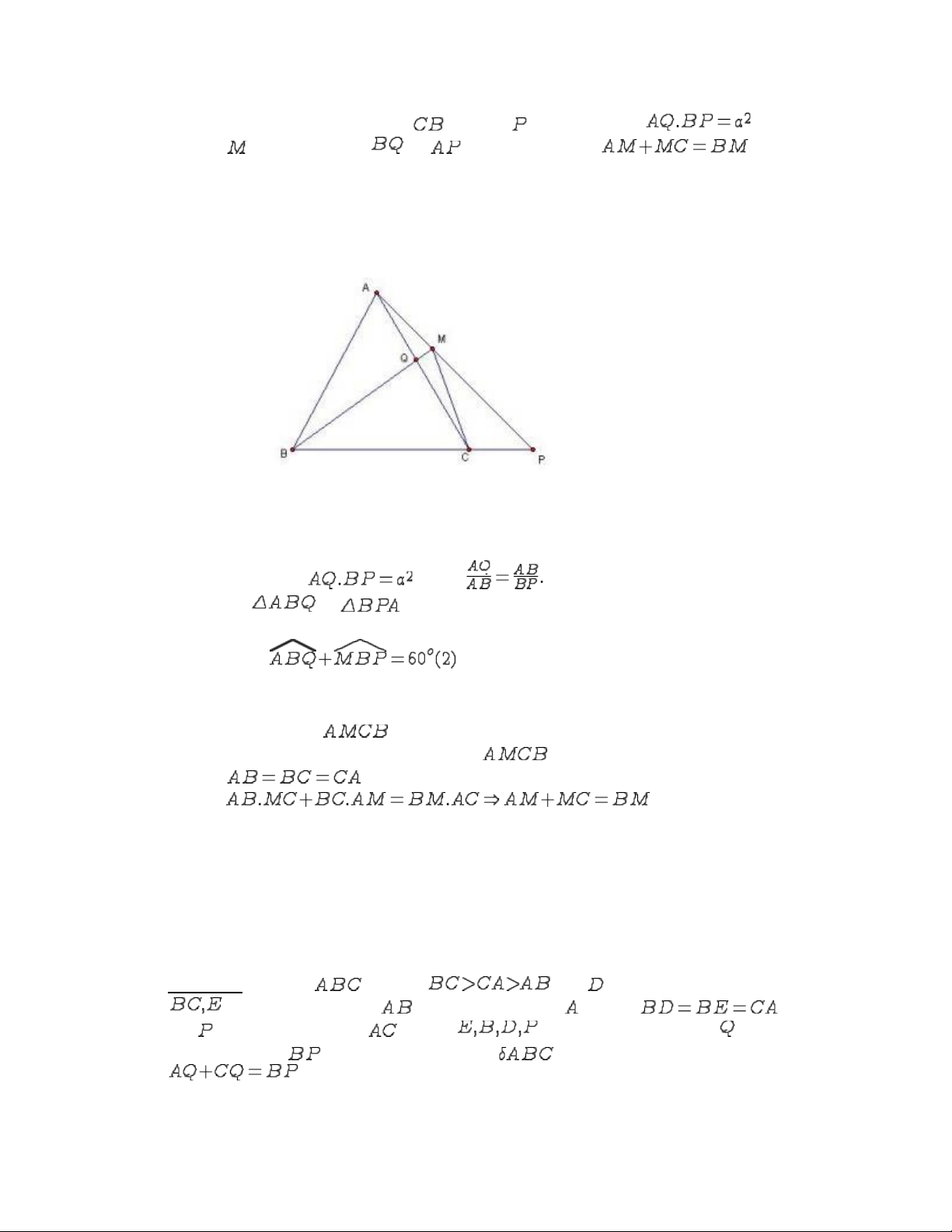di động, trên tia đối của tia lấy điểm di động sao cho . Gọi là giao điểm của và . Chứng minh rằng: ( Đề thi vào trường THPT chuyên Lê QuíĐôn, thị xãĐông Hà, tỉnh Quảng Trị, năm học 2005-2006)Hình minh họa (hình 3)Chứng minh:Từ giả thiết suy ra Xét và có: Lại cóTừ: Suy ra tứ giác nội tiếp được đường tròn.Áp dụng định lí Ptô-lê-mê cho tứ giác nội tiếp và giả thiết ta có:(đpcm) Đây là 1 bài toán khá dễ và tất nhiên cách giải này ko được đơn giản lắm.Vì nếu muốn sử dụng đẳng thức Ptô-lê-mê trong 1 kì thi thì có lẽ phải chứng minh nó dưới dạng bổ đề. Nhưng điều chú ýởđây là ta chẳng cần phải suy nghĩ nhiều khi dùng cách trên trong khi đó nếu dùng cách khác thì lời giải có khi lại ko mang vẻ tường minh.Bài toán 2: Tam giác vuông có . Gọi là một điểm trên cạnh là một điểm trên cạnh kéo dài về phía điểm sao cho . Gọi là một điểm trên cạnh sao cho nằm trên một đường tròn. là giao điểm thứ hai của với đường tròn ngoại tiếp . Chứng minh rằng: (Đề thi chọn đội tuyển Hồng Kông tham dự IMO 2000, HongKong TST 2000) 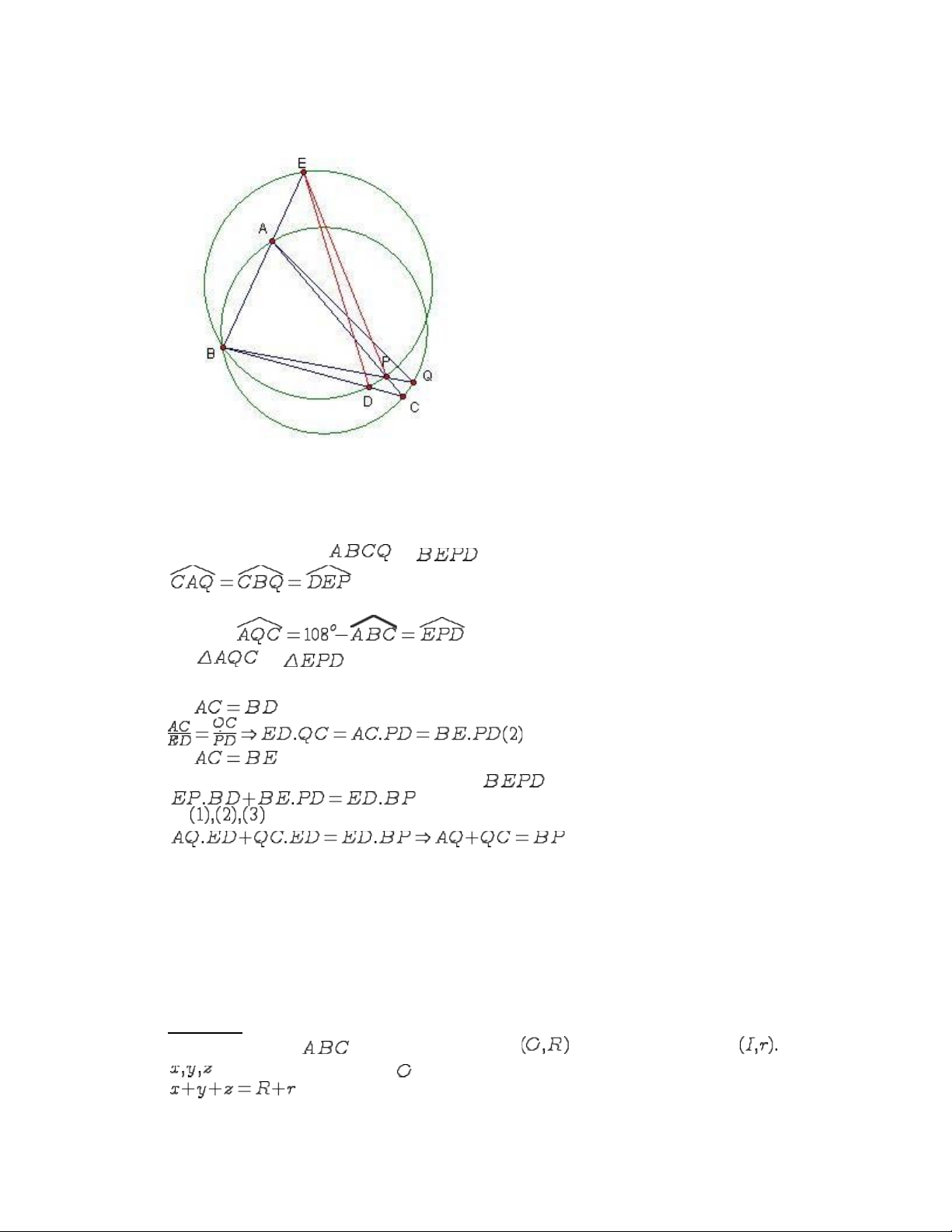Hình minh họa: (hinh 4)Chứng minh:Xét các tứ giác nội tiếp và ta có:(cùng chắn các cung tròn)Mặt khác Xét và có:(do )(do )Áp dụng định lí Ptô-lê-mê cho tứ giác nội tiếp ta có: Từ suy ra:(đpcm)Có thể thấy rằng bài 1 là tư tưởng đơn giản để ta xây dựng cách giải của bài 2. Tức là dựa vào các đại lượng trong tam giác bằng nhau theo giả thiết ta sử dụng tam giác đồng dạng để suy ra các tỉ số liên quan và sử dụng phép thếđể suy ra điều phải chứng minh. Cách làm này tỏ ra khá là hiệu quả và minh họa rõ ràng qua 2 ví dụ mà zaizai đã nêu ở trên. Để làm rõ hơn phương pháp chúng ta sẽ cùng nhau đến với việc chứng minh 1 định lí bằng chính Ptô-lê-mê.Bài toán 3: ( Định lí Carnot)Cho tam giác nhọn nội tiếp trong đường tròn và ngoại tiếp đường tròn Gọi lần lượt là khoảng cách từ tới các cạnh tam giác. Chứng minh rằng:

Tài liệu liên quan

Một phương pháp cải thiện độ chính xác của mô hình học sâu phát hiện bệnh u não trên ảnh cộng hưởng từ

8 trang

Sử dụng phương pháp Markov Chain Monte Carlo ước lượng hàm mũ ma trận

9 trang

Chuyên đề dãy số - Giải các hệ thức truy hồi

21 trang

Đề tài: Quá trình ra đề kiểm tra trong chủ đề Dãy số, cấp số cộng và cấp số nhân

16 trang

Syllabus: Elementary Statistics

6 trang

Thể tích và diện tích của hình cầu n chiều - Phải chăng kích thước vũ trụ chỉ bằng 1 điểm vô hạn chiều

6 trang

Chuyên san số 2: Tổng điều tra cơ sở kinh tế, hành chính, sự nghiệp năm 2007

14 trang

Xác định khối lượng hàng hóa bằng phương pháp xác định mớn nước

W 26 trang

Phương pháp chia hỗn hợp thành hai phần không đều nhau

W 5 trang

FEM for Elliptic problems

8 trang

Tài liêu mới

Bài tập Xác suất thống kê - Trường Đại học Kiến trúc Hà Nội

18 trang

Bài tập xác suất và thống kê

55 trang

Bài tập Lý thuyết xác suất và thống kê

31 trang

Bài giảng Toán kỹ thuật: Chương 5 - Đỗ Đắc Thiểm

6 trang

Bài giảng Toán kỹ thuật: Chương 4 - Đỗ Đắc Thiểm

19 trang

Bài giảng Toán kỹ thuật: Chương 3 - Đỗ Đắc Thiểm

14 trang

Bài giảng Toán kỹ thuật: Chương 2 - Đỗ Đắc Thiểm

15 trang

Bài giảng Toán kỹ thuật: Chương 1 - Đỗ Đắc Thiểm

51 trang

Bài giảng Toán kinh tế - Chương 6: Bài toán vận tải

34 trang

Bài giảng Toán kinh tế - Chương 5: Bài toán quy hoạch tuyến tính

53 trang

Bài giảng Toán kinh tế - Chương 4: Tối ưu hóa sản xuất và tiêu dùng

28 trang

Bài giảng Toán kinh tế - Chương 3: Phân tích so sánh

19 trang

Bài giảng Toán kinh tế - Chương 2: Phân tích cân bằng tĩnh

9 trang

Bài giảng Toán kinh tế - Chương 1: Giới thiệu mô hình toán kinh tế

14 trang

Hàm giả đảo giải hệ phương trình tuyến tính bằng lập trình Python và ứng dụng

11 trang

AI tóm tắt

- Giúp bạn nắm bắt nội dung tài liệu nhanh chóng!

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Giới thiệu

Về chúng tôi

Việc làm

Quảng cáo

Liên hệ

Chính sách

Thoả thuận sử dụng

Chính sách bảo mật

Chính sách hoàn tiền

DMCA

Hỗ trợ

Hướng dẫn sử dụng

Đăng ký tài khoản VIP

Zalo/Tel:

093 303 0098

Email:

[email protected]

Phương thức thanh toán

Theo dõi chúng tôi

Facebook

Youtube

TikTok

Chịu trách nhiệm nội dung: Nguyễn Công Hà Doanh nghiệp quản lý: Công ty TNHH Tài Liệu trực tuyến Vi Na - GCN ĐKDN: 0307893603 Địa chỉ: 54A Nơ Trang Long, P. Bình Thạnh, TP.HCM - Điện thoại: 0283 5102 888 - Email: [email protected]ấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015