Định Lý Sin – Wikipedia Tiếng Việt
Có thể bạn quan tâm

| Lượng giác |
|---|
 |
|
| Tham khảo |
|
| Định lý |
|
| Vi tích phân |
|
|
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng và bán kính đường tròn ngoại tiếp. Định lý sin được biểu diễn dưới dạng
.trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:
Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó. Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.
Các ví dụ
[sửa | sửa mã nguồn]Cho: cạnh a = 20, cạnh c = 24, góc C = 40°
Theo định lý sin ta có
Một ví dụ khác:
Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:
và
Vấn đề tính toán
[sửa | sửa mã nguồn]Giống như định lý cos, mặc dù định lý sin đúng về mặt toán học, nhưng việc áp dụng có thể dẫn đến sai số lớn khi sin của một góc rất gần với 1.
Vài ứng dụng
[sửa | sửa mã nguồn]- Định lý sin có thể được dùng để chứng minh công thức sin của một tổng khi hai góc α và β nằm giữa 0 và 90 độ.
- Định lý sin cũng có thể được dùng để chứng minh định lý tang và công thức Mollweide (Dresden 2009, Plane Trigonometry trang 76–78).[cần dẫn nguồn]
Trường hợp đặc biệt
[sửa | sửa mã nguồn]Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.
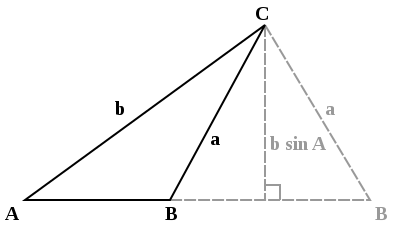
Điều kiện để tam giác ABC rơi vào trường hợp này là:
- Chỉ biết cạnh ‘’a’’, ‘’b’’ và góc A.
- Góc A nhọn (A < 90°).
- Cạnh a bé hơn cạnh b (a < b).
- Cạnh ‘’a’’ dài hơn đường cao của tam giác vuông có góc ‘’A’’ và cạnh huyền ‘’b’’ (a > b sin A).
Trong trường hợp đó, góc ‘’B’’ có thể nhọn hoặc tù, do đó:
hoặc
Liên quan với đường tròn ngoại tiếp
[sửa | sửa mã nguồn]Trong công thức
giá trị của mỗi phân số chính là đường kính của đường tròn ngoại tiếp tam giác đó.[1] Người ta cũng chứng minh được rằng giá trị trên bằng
trong đó S là diện tích của tam giác và s là nửa chu vi của nó.
Công thức thứ hai có sử dụng đến công thức Heron.
Các dạng khác
[sửa | sửa mã nguồn]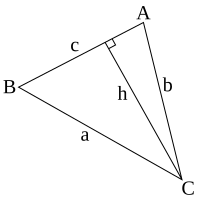
Từ hình vẽ bên, ta nhận thấy:
Do đó
và
Làm tương tự, ta có:
Diện tích tam giác được tính bởi công thức
Nhân hai vế với ta được
Định lý sin trong tứ diện
[sửa | sửa mã nguồn]
Một hệ quả của định lý sin là: trong tứ diện OABC ta có
Xem thêm
[sửa | sửa mã nguồn]- Định lý cos
- Định lý tang
- Công thức Mollweide
- Công thức nửa cạnh
Tham khảo
[sửa | sửa mã nguồn]- ^ Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 1-3, 1967
Liên kết ngoài
[sửa | sửa mã nguồn]- The Law of Sines
- Degree of Curvature
- Finding the Sine of 1 Degree
Từ khóa » Công Thức Cosin
-
Định Lí Cosin, định Lý Sin, Các Công Thức Tính Diện Tích Tam Giác - Mathvn
-
Định Lý Sin, Cos Và Công Thức Sin Cos Trong Tam Giác Chi Tiết Từ A - Z
-
Định Lí Sin, Định Lí Côsin, Diện Tích Tam Giác - Công Thức Học Tập
-
Định Lí Côsin Và Cách Vận Dụng định Lý Côsin Trong Tam Giác Cực Hay
-
Các Công Thức Lượng Giác Toán 10 Đầy Đủ Nhất - Kiến Guru
-
Định Lí Cosin, định Lý Sin, Các Công Thức Tính Diện Tích Tam Giác
-
Định Lý Và Công Thức Sin Cos Tan Lớp 9, Lớp 10, Lớp 11, Lớp 12
-
Định Lí Sin, Định Lí Côsin, Diện Tích Tam Giác - Mobitool
-
Định Lý Sin, Cos Và Công Thức Sin Cos Trong Tam Giác Chi Tiết Từ A – Z
-
Lý Thuyết Các Hệ Thức Lượng Trong Tam Giác Và Giải Tam Giác
-
Cách Vận Dụng định Lý Côsin Trong Tam Giác










![{\displaystyle {\begin{aligned}{\frac {abc}{2S}}&{}={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\[6pt]&{}={\frac {2abc}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/336eb56ff0d35b43fb73b79862cd47aa988b48de)









