Định Lý Talet Trong Tam Giác, Tính Chất đường Phân Giác - Abcdonline
Có thể bạn quan tâm
1. Tỉ số của hai đoạn thẳng
• Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
• Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo.
2. Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức:
![]()
3. Định lí Ta-lét trong tam giác
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
B’C’//BC thì ![]()
4. Định lí Ta-lét đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
![]() ⇒ B’C’//BC
⇒ B’C’//BC
5. Hệ quả
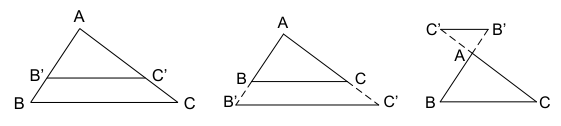
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Nếu B’C’//BC thì ![]()
Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.
6. Tính chất đường phân giác trong tam giác
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
AD, AE là các phân giác trong và ngoài của góc ![]() ⇒
⇒ ![]()
7. Nhắc lại một số tính chất của tỉ lệ thức
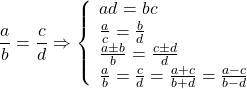
Đa giác lồi, đa giác đều, diện tích đa giác
Định nghĩa, tính chất, dấu hiệu nhận biết hình vuông
Định nghĩa, tính chất, dấu hiệu nhận biết hình thoi
Định nghĩa, tính chất, dấu hiệu nhận biết hình chữ nhật
Cách chứng minh tứ giác là hình bình hành – Toán 8
Đường trung bình của tam giác, của hình thang
Định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân
Từ khóa » định Lý Talet đảo Trong Tam Giác Vuông
-
Lý Thuyết định Lí đảo Và Hệ Quả Của định Lí Talet | SGK Toán Lớp 8
-
Định Lí đảo Và Hệ Quả Của định Lí Ta-lét
-
Định Lý Talet Và Talet đảo Trong Tam Giác, Tam Giác Vuông Toán ...
-
Định Lý Talet Thuận, định Lý Talet đảo Và Hệ Quả Của định Lý Talet
-
Định Lý Talet Và Những Hệ Quả Của định Lý Talet
-
Định Lí Ta-lét. Định Lí đảo Và Hệ Quả Của định Lí Ta-lét
-
Bài 2 : Định Lí Talet đảo – Các Hệ Quả. | Toán Học Phổ Thông - SGK
-
Định Lí Ta Lét Trong Tam Giác Và Những Hệ Quả Bạn Cần Biết
-
Định Lý Ta Lét Là Gì? Những Hệ Quả Của định Lý Talet
-
Định Lý Thales – Wikipedia Tiếng Việt
-
Lý Thuyết định Lí Ta-lét. định Lí đảo Và Hệ Quả Của định Lí Ta-lét Toán 8
-
Định Lí Talet đảo Và Hệ Quả Của định Lí Talet
-
Định Lý Talet Và Các Hệ Quả Trong Tam Giác (định Lý Talet đảo)