Định Lý Trục Quay Song Song – Wikipedia Tiếng Việt

Định lý trục quay song song hay còn gọi là định lý Steiner-Huygens, định lý dời trục, công thức dời trục là định lý dùng để tính mômen quán tính của các vật nếu trục quay z không đi qua khối tâm của vật.

Nội dung

[sửa | sửa mã nguồn]

Mômen quán tính của một vật rắn đối với một trục nào đó bằng mômen quán tính của vật rắn đối với trục song song đi qua khối tâm cộng với tích số của khối lượng vật rắn và bình phương khoảng cách giữa hai trục.[1]

Công thức

[sửa | sửa mã nguồn]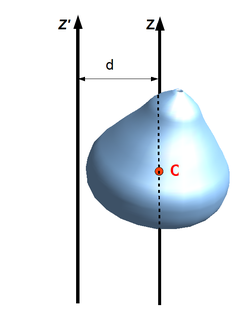

Giả sử trục quay Z' song song với trục quay Z đi qua khối tâm C và giả sử khoảng cách giữa hai trục này là d. Có thể chứng minh được:

I Z ′ = I C + m d 2 {\displaystyle I_{Z}'=I_{C}+md^{2}}

Trong đó:

Iz' là mômen quán tính của vật đối với trục quay Z' Ic là mômen quán tính của vật đối với trục quay Z, đi qua khối tâm C m là khối lượng của vật

Mômen quán tính của một vật rắn đối với một trục nào đó bằng mômen quán tính của vật rắn đối với trục song song đi qua khối tâm cộng với tích số của khối lượng vật rắn và bình phương khoảng cách giữa hai trục.

Chứng minh

[sửa | sửa mã nguồn]

Chúng ta giả sử, nhưng không mất đi tính chất tổng quát, rằng trong hệ tọa độ Descartes khoảng cách d giữa 2 trục song song nằm dọc theo trục x và khối tâm ở trung điểm. Mômen quán tính đối với trục Z sẽ là:

I c m = ∫ ( x 2 + y 2 ) d m . {\displaystyle I_{\mathrm {cm} }=\int (x^{2}+y^{2})\,dm.}

Mômen quán tính đối với trục Z′, với khoảng cách d tử khối tâm trên trục x sẽ là:

I = ∫ [ ( x − d ) 2 + y 2 ] d m . {\displaystyle I=\int \left[(x-d)^{2}+y^{2}\right]\,dm.}

Sau khi khai triển bình phương:

I = ∫ ( x 2 + y 2 ) d m + d 2 ∫ d m − 2 d ∫ x d m . {\displaystyle I=\int (x^{2}+y^{2})\,dm+d^{2}\int dm-2d\int x\,dm.}

Tích phân phần đầu sẽ là Icm và tích phân thứ nhì sẽ là md2. Tích phân của phần cuối (khối tâm) – sẽ là số không (zero) bời vi khối tâm nằm ở trung điểm. Do đó phương trính trên sẽ trở thành:

I = I c m + m d 2 . {\displaystyle I=I_{\mathrm {cm} }+md^{2}.}

Ứng dụng

[sửa | sửa mã nguồn]

Ví dụ 1: Mômen quán tính của một cây gậy (a rod) với khối lượng m và chiều dài L đối với trục quay 1 là:

I 1 = 1 12 m L 2 {\displaystyle I_{1}={\frac {1}{12}}mL^{2}}

Mômen quán tính của cây gậy đó đối với trục quay 2 là:

I 2 = 1 12 m L 2 + m ( L 2 ) 2 = 1 3 m L 2 {\displaystyle I_{2}={\frac {1}{12}}mL^{2}+m\left({\frac {L}{2}}\right)^{2}={\frac {1}{3}}mL^{2}}

Ví dụ 2: Mômen quán tính của một cái dĩa (a disk) với khối lượng m và bán kính R, đối với trục quay 1 là:

I 1 = 1 2 m R 2 {\displaystyle I_{1}={\frac {1}{2}}mR^{2}}

Mômen quán tính của cái dĩa đó đối với trục quay 2 là:

I 2 = 1 2 m R 2 + m R 2 = 3 2 m R 2 {\displaystyle I_{2}={\frac {1}{2}}mR^{2}+mR^{2}={\frac {3}{2}}mR^{2}}

Ví dụ 3: Mômen quán tính của một chiếc vòng (a ring) có khối lượng m, bán kính trong R_1 và bán kính ngoài R_2, đối với trục quay 1 là:

I 1 = 1 2 m ( R 1 2 + R 2 2 ) {\displaystyle I_{1}={\frac {1}{2}}m\left(R_{1}^{2}+R_{2}^{2}\right)}

Mômen quán tính của chiếc vòng đó đối với trục quay 2 là:

I 2 = 1 2 m ( R 1 2 + R 2 2 ) + m ( R 1 + R 2 2 ) 2 {\displaystyle I_{2}={\frac {1}{2}}m\left(R_{1}^{2}+R_{2}^{2}\right)+m\left({\frac {R_{1}+R_{2}}{2}}\right)^{2}}

Xem thêm

[sửa | sửa mã nguồn]

• Mômen quán tính

Tham khảo

[sửa | sửa mã nguồn]

1. ^ Halliday, Resnick, Walker, Principles of Physics, 9th edition, International student version, John Wiley & Son, 2011, ISBN 978-0-470-56158-4, trang 254

Bài viết về chủ đề vật lý này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn.

• x
• t
• s

Thế loại:Cơ học