Định Nghĩa Và Phân Loại Về Khối đa Diện đều - CungHocVui
Có thể bạn quan tâm

Đăng nhập hoặc đăng ký miễn phí để đặt câu hỏi và nhận câu trả lời sớm nhất !
- Đăng nhập
- hoặc
- Đăng kí
- Tiểu học
- Lớp 5
- Tiếng Anh lớp 5 Mới
- Tiếng Việt lớp 5
- Toán lớp 5
- Lịch sử lớp 5
- Địa lí lớp 5
- Khoa học lớp 5
- Lớp 4
- Toán lớp 4
- Tiếng Việt lớp 4
- Khoa học lớp 4
- Lịch sử lớp 4
- Địa lí lớp 4
- Lớp 3
- Toán lớp 3
- Tiếng Việt lớp 3
- Tiếng Anh lớp 3 Mới
- Lớp 2
- Tiếng Việt lớp 2
- Toán lớp 2
- Tiếng việt 2 mới Cánh Diều
- Tiếng việt 2 mới Chân trời sáng tạo
- Tiếng việt 2 mới Kết nối tri thức
- Giải toán 2 mới Cánh Diều
- Giải toán 2 mới Chân trời sáng tạo
- Giải toán 2 mới Kết nối tri thức
- Tiếng anh 2 mới Explore our world
- Tiếng anh 2 mới Family and Friends
- Tiếng anh 2 mới Kết nối tri thức
- Đạo đức 2 mới Cánh Diều
- Đạo đức 2 mới Chân trời sáng tạo
- Đạo đức 2 mới Kết nối tri thức
- Tự nhiên xã hội lớp 2 Cánh Diều
- Tự nhiên xã hội lớp 2 Chân trời sáng tạo
- Tự nhiên xã hội lớp 2 Kết nối tri thức
- Lớp 5
- Công thức
- Công thức Toán học
- Công thức Sinh học
- Công thức Hóa học
- Công thức Vật lý
- Công thức Địa Lý
- Đề thi & kiểm tra
- Phương trình hóa học
- Tuyển sinh
- Thông tin trường
- Tư vấn tuyển sinh
- Tin tức tuyển sinh
- Review Sách
- Review Ứng dụng

- Tiểu học
- Lớp 5
- Tiếng Anh lớp 5 Mới
- Tiếng Việt lớp 5
- Toán lớp 5
- Lịch sử lớp 5
- Địa lí lớp 5
- Khoa học lớp 5
- Lớp 4
- Toán lớp 4
- Tiếng Việt lớp 4
- Khoa học lớp 4
- Lịch sử lớp 4
- Địa lí lớp 4
- Lớp 3
- Toán lớp 3
- Tiếng Việt lớp 3
- Tiếng Anh lớp 3 Mới
- Lớp 2
- Tiếng Việt lớp 2
- Toán lớp 2
- Tiếng việt 2 mới Cánh Diều
- Tiếng việt 2 mới Chân trời sáng tạo
- Tiếng việt 2 mới Kết nối tri thức
- Giải toán 2 mới Cánh Diều
- Giải toán 2 mới Chân trời sáng tạo
- Giải toán 2 mới Kết nối tri thức
- Tiếng anh 2 mới Explore our world
- Tiếng anh 2 mới Family and Friends
- Tiếng anh 2 mới Kết nối tri thức
- Đạo đức 2 mới Cánh Diều
- Đạo đức 2 mới Chân trời sáng tạo
- Đạo đức 2 mới Kết nối tri thức
- Tự nhiên xã hội lớp 2 Cánh Diều
- Tự nhiên xã hội lớp 2 Chân trời sáng tạo
- Tự nhiên xã hội lớp 2 Kết nối tri thức
- Lớp 5
- Công thức
- Công thức Toán học
- Công thức Sinh học
- Công thức Hóa học
- Công thức Vật lý
- Công thức Địa Lý
- Đề thi & kiểm tra
- Phương trình hóa học
- Tuyển sinh
- Thông tin trường
- Tư vấn tuyển sinh
- Tin tức tuyển sinh
- Review Sách
- Review Ứng dụng
Toán lớp 12
PHẦN GIẢI TÍCH - TOÁN 12
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Bài 1. Sự đồng biến, nghịch biến của hàm số
Bài 2. Cực trị của hàm số
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 4. Đường tiệm cận
Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Ôn tập Chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm sô
CHƯƠNG II. HÀM SỐ LŨY THỪA HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài 1. Lũy thừa
Xem Thêm Định nghĩa và phân loại về khối đa diện đềuĐịnh nghĩa và phân loại về khối đa diện đều
Bài viết dưới đây Cunghocvui sẽ giúp các bạn làm quen với các khái niệm các khối đa diện đều!
I. Khái niệm chung
Khối ĐD là các hình khối có các mặt bên là các đa giác đều, ví dụ như: tam giác đều, tứ giác đều, lục giác đều, ngũ giác đều,...
Phân loại: ĐD đều lồi và ĐD đều lõm.
II. Bảng khối đa diện đều
- Đa diện lồi
| Năm khối đa diện đều | ||||
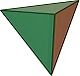
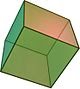
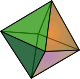
| Tứ diện đều | Khối lập phương | Khối bát diện đều | Khối mười hai mặt đều | Khối hai mươi mặt đều |
| Khối ĐD đều loại 3 3 | Khối đa diện đều loại 4 3 | Khối ĐD đều loại 3 4 | Khối đa diện đều 5 3 | Khối ĐD đều 3 5 |
Tên của chúng gọi theo số mặt của mỗi khối tương ứng là 4, 6, 8, 12, và 20.
Khối đa diện và bộ công thức tính thể tính đa diện không thể bỏ qua
- Tứ diện đều:
+ Nhận dạng: 4 mặt của tư diện là các tam giác đều.
+ Tư diện đều có đặc điểm như hình chóp tam giác đều.
+ Công thức tính thể tích: \(V=\dfrac{a^3\sqrt{2}}{12}.\)
+ Công thức tính thể tích: \(h=\dfrac{a\sqrt{6}}{3}\)
- Khối lập phương:
+ Khối lập phương là một khối đa diện đều ba chiều có 6 mặt đều là hình vuông, có 12 cạnh bằng nhau, 8 đỉnh, cứ 3 cạnh gặp nhau tại 1 đỉnh, có 4 đường chéo cắt nhau tại một điểm.
+ Khối lập phương là tập hợp những điểm nằm bên trong và các điểm nằm trên các mặt, cạnh, đỉnh này.
+ Khối lập phương là khối 6 mặt đều duy nhất và là 1 trong 5 khối đa diện đều, với 9 mặt đối xứng.
Nếu cạnh của khối lập phương là a
| diện tích bề mặt | \({\displaystyle 6a^{2}}\) |
| thể tích | \({\displaystyle a^{3}}\) |
| bán kính mặt cầu ngoại tiếp | \({\displaystyle {\dfrac {{\sqrt {3}}a}{2}}}\) |
| bán kính mặt cầu tiếp xúc với các cạnh | \({\displaystyle {\dfrac {a}{\sqrt {2}}}}\) |
| bán kính mặt cầu nội tiếp | \({\displaystyle {\dfrac {a}{2}}}\) |
- Khối bát diện đều:
Định nghĩa của hình bát diện đều sẽ bắt nguồn từ định nghĩa của khối đa diện đều, cụ thể như sau:
+ Khối đa diện đều là một khối đa diện có tất cả các mặt là các đa giác đều bằng nhau và các cạnh bằng nhau. Và đa diện đều được chia thành đa diện đều lồi và đa diện đều lõm
+ Hình bát diện đều là một trong những hình thuộc thành phần của khối đa diện đều. Ngoài bát diện đều thì còn có những khối đa diện đều khác như là: hình tứ diện đều, hình lập phương, hình mười hai mặt đều, hình hai mươi mặt đều.
- Khối hai mươi mặt đều:
+ Mỗi mặt là một tam giác đều
+ Mỗi đỉnh là đỉnh chung của 5 mặt
+ Diện tích của tất cả các mặt khối 20 mặt đều là \(S=5√3a^2\)
+ Thể tích khối 20 mặt đều cạnh a là \(V=\dfrac{5(3+√5)a^3}{12}.\)
+ Bán kính mặt cầu ngoại tiếp là \(R=\dfrac{a(√10+2√5)}{4}.\)
- Tính chất:
Một khối đa diện lồi là đều nếu và chỉ nếu thỏa mãn cả ba tính chất sau
- Tất cả các mặt của nó là các đa giác đều, bằng nhau
- Các mặt không cắt nhau ngoài các cạnh
- Mỗi đỉnh là giao của một số mặt như nhau (cũng là giao của số cạnh như nhau).
Mỗi khối đa diện đều có thể xác định bới ký hiệu {p, q} trong đó
p = số các cạnh của mỗi mặt (hoặc số các đỉnh của mỗi mặt)
q = số các mặt gặp nhau ở một đỉnh (hoặc số các cạnh gặp nhau ở mỗi đỉnh).
II. Trả lời câu hỏi
1. Khối lập phương là khối ĐD đều nào? Đáp án: 4 3.
2. Khối đa diện 12 mặt đều thuộc loại nào? Đáp án: Loại 5 3.
3. Khối đa diện đều loại 5 3 có mặt là? Đáp án: Ngũ giác.
4. Khối đa diện đều loại 3 3 có bao nhiêu trục đối xứng? Đáp án: 3
Trên đây là toàn bộ kiến thức mà Cunghocvui muốn chia sẻ. Hy vọng rằng sau bài viết các bạn đã có thể trả lời đươc câu hỏi có bao nhiêu khối đa diện đều và học được cách nhớ 5 loại khối đa diện đều lồi!
Tags khái niệm các khối đa diện đều khối lập phương là khối đa diện đều thuộc loại khối đa diện 12 mặt đều thuộc loại nào khối đa diện đều loại 3 3 có bao nhiêu trục đối xứng khối đa diện đều loại 5 3 có mặt là cách nhớ 5 loại khối đa diện đều bảng khối đa diện đều khối đa diện đều loại 5 3 khối đa diện đều loại 4 3 có bao nhiêu khối đa diện đều khối đa diện đều Bài trướcCó thể bạn quan tâm
Câu hỏi 4 trang 18 SGK Hình học 12
Bài 2 trang 18 SGK Hình học 12
Bài 3 trang 18 SGK Hình học 12
Bài trướcBài 4 trang 18 SGK Hình học 12
Bạn muốn xem thêm với- Câu hỏi 1 trang 15 SGK Hình học 12
- Câu hỏi 2 trang 16 SGK Hình học 12
- Câu hỏi 3 trang 17 SGK Hình học 12
- Bài 1 trang 18 SGK Hình học 12
- Câu hỏi 4 trang 18 SGK Hình học 12
- Bài 2 trang 18 SGK Hình học 12
- Bài 3 trang 18 SGK Hình học 12
- Bài 4 trang 18 SGK Hình học 12
Email: [email protected]
Liên hệGiới thiệu
Về chúng tôi Điều khoản thỏa thuận sử dụng dịch vụ Câu hỏi thường gặpChương trình học
Hướng dẫn bài tập Giải bài tập Phương trình hóa học Thông tin tuyển sinh Đố vuiĐịa chỉ: 102, Thái Thịnh, Trung Liệt, Đống Đa, Hà Nội
Email: [email protected]
Copyright © 2021 CungHocVui
 Xem. Đặt câu hỏi. Trả lời.
Xem. Đặt câu hỏi. Trả lời. Từ khóa » Cách Nhớ Các Loại đa Diện đều
-
Cách Ghi Nhớ Số đỉnh, Số Cạnh Và Số Mặt Của 5 Khối đa Diện đều - Vted
-
MẸO NHỚ SỐ ĐỈNH, CẠNH, MẶT CỦA 5 KHỐI ĐA DIỆN ĐỀU LOẠI {p
-
Cách Nhớ 5 Loaij Khối đa Diện đều Dễ Nhất - YouTube
-
Mẹo Nhớ Nhanh Số MẶT - ĐỈNH - CẠNH Các Khối đa Diện đều Trong ...
-
Cách Nhớ 5 Loại Khối đa Diện đều - Hỏi Đáp
-
MẸO NHỚ SỐ ĐỈNH, CẠNH, MẶT CỦA 5 KHỐI ĐA DIỆN ĐỀU LOẠI ...
-
Cách Nhớ Các Khối đa Diện đều
-
Toán Cấp 3 - Cách Nhớ Dễ Nhất 5 Khối đa Diện. Kiến Thức... | Facebook
-
Số đỉnh, Số Cạnh, Số Mặt Của 5 Khối đa Diện đều - MathVn.Com
-
Số đỉnh Của Bát Diện đều - Randy-rhoads
-
LÀM CHỦ KIẾN THỨC ĐỊNH TÍNH VỀ KHỐI ĐA DIỆN QUA SƠ ĐỒ ...
-
Khối đa Diện đều – Wikipedia Tiếng Việt
-
Cách Gấp Khối đa Diện 12 Mặt đều