Độ Lệch Chuẩn (Standard Deviation) Là Gì? Công Thức Tính Ra Sao?

Độ lệch chuẩn là những kiến thức quan trọng trong toán học liên quan đến tính toán, thống kê, báo cáo. Cùng tìm hiểu công thức tính ra sao và ví dụ về nó nhé.

Bài viết hôm nay, chúng tôi sẽ khái quát và giúp bạn đọc hiểu chi tiết về khái niệm độ lệch chuẩn là gì? Cũng như công thức, các bước sử dụng độ lệch chuẩn và sử dụng độ lệch chuẩn như thế nào,vv… Đừng bỏ qua kiến thức quan trọng này bởi bạn có thể áp dụng nó vào rất nhiều lĩnh vực trong đời sống.

Mục Lục

• 1 Độ lệch chuẩn là gì?
• 2 Công thức tính độ lệch chuẩn
• 3 Các bước tính độ lệch chuẩn
  • 3.1 Tính trung bình
  • 3.2 Tính phương sai
  • 3.3 Tính độ lệch chuẩn
• 4 Sử dụng độ lệch chuẩn như thế nào?
• 5 Ví dụ về độ lệch chuẩn
• 6 Độ lệch chuẩn và phương sai
• 7 Kết luận

Độ lệch chuẩn là gì?

Độ lệch chuẩn hay còn gọi là Standard Deviation. Là đại lượng dùng để phản ánh độ phân tán của các giá trị trong bộ dữ liệu. Thể hiện sự biến thiên của giá trị trong một thời điểm phản ánh xu thế của sự thay đổi.

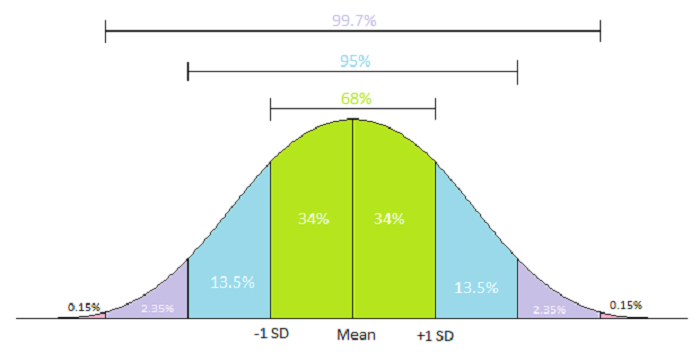
Thông qua độ lệch chuẩn các nhà kinh tế, nhà quản lý có thể quan sát dự báo các thời kỳ biến động của nền kinh tế. Đối với các lĩnh vực khác cũng tương tự, độ lệch chuẩn luôn phân tích tính ổn định hoặc sự thay đổi cụ thể nào đó.

Xem thêm:

• Phân kỳ là gì? 3 dạng phân kỳ phổ biến nhất
• Năng lực cốt lõi là gì? Tiêu chí xác định

Công thức tính độ lệch chuẩn

Công thức tính độ lệch chuẩn được thể hiện dưới dạng công thức:

Trong đó:

• xi: Là giá trị của điểm i trong tập dữ liệu.
• x̄: Là giá trị của tập dữ liệu.
• n: Là tổng số quan sát trong tập dữ liệu.

Giá trị x trung bình sẽ được tính bằng cách tổng tất cả các quan sát và chia cho số quan sát.

Phương sai được tính cho mỗi điểm dữ liệu bằng cách: Trừ giá trị của quan sát với giá trị trung bình. Kết quả sau đó được bình phương và được chia cho số quan sát trừ một.

Căn bậc hai của phương sai lên để tìm độ lệch chuẩn.

Các bước tính độ lệch chuẩn

Tính trung bình

Để tính giá trị trung bình chúng ta sẽ lấy tổng các giá trị trong một bộ dữ liệu xác định chia cho tổng số những giá trị mà chúng ta có trong bộ dữ liệu đó.

Ví dụ: Tập hợp các điểm cho một bài kiểm tra là: 10, 8, 10, 8, 8, và 4.

=> Tính giá trị trung bình: Lấy trung bình cộng của 10, 8, 10, 8, 8, và 4. Bạn thấy có 6 số liệu trong tập hợp điểm kiểm tra này và tổng của các số đó là 48. Như vậy kết quả trung bình cộng thu được là  48 / 6 = 8.

Tính phương sai

Chúng ta sẽ được chia ra nhiều bước vì tính phương sai khá phức tạp và cần cẩn thận.

Bước 1: Đầu tiên, lấy giá trị trung bình đã được được tính ở trên trừ đi từng giá trị cụ thể trong bộ dữ liệu. Như thế chúng ta sẽ có kết quả là khoảng cách của từng giá trị so với giá trị trung bình đã tìm được.

Bước 2: Bình phương những giá trị vừa được tính khi thực hiện phép trừ ở bên trên.

Ví dụ với tập hợp các điểm 10, 8, 10, 8, 8, và 4 và giá trị trung bình là 8. Khi bình phương các phép trừ sẽ theo thứ tự là 4, 0, 4, 0, 0, và 16.

Bước 3: Tìm tổng bình phương bằng cách cộng tất cả các giá trị sau khi bình phương ở trên. 

Tập hợp các số liệu ban đầu chúng ta có được tổng bình phương là: 4 + 0 + 4 + 0 + 0 + 16 = 24.

Bước 4: Tìm được phương sai bằng cách đem tổng bình phương chia cho một số cụ thể. Số này được tính bằng cách lấy tổng số các giá trị trừ đi 1.

Với tập hợp điểm kiểm tra ban đầu chúng ta có tổng số các giá trị là 6, tổng bình phương là 24. Vậy phương sai của bộ số liệu này là kết quả của phép tính 24/ (6-1) = 4,8.

Tính độ lệch chuẩn

Độ lệch chuẩn sẽ được tính bằng căn bậc 2 của phương sai. Sau khi đã tính được phương sai thì chúng ta sẽ dễ dàng tính được độ lệch chuẩn.

Trong bộ dữ liệu chúng ta đã chọn ban đầu. Với giá trị phương sai là 4, 8.

=> Giá trị của độ lệch chuẩn sẽ là: √4,8 = 2,19.

Có thể bạn quan tâm:  Mining City là gì? Sự thật về Mining City lừa đảo người chơi hay không?

Sử dụng độ lệch chuẩn như thế nào?

Trong các thị trường chứng khoán, đầu tư việc bạn áp dụng cách tính toán độ lệch chuẩn trong các giao dịch, tính toán là điều vô cùng hữu ích. Vì nó sẽ giúp bạn đo lường mức độ biến động của thị trường và chứng khoán. Và có thể dự đoán được hiệu quả trong đầu tư.

Đối với các quỹ tăng trưởng tích cực thường có độ lệch chuẩn cao hơn so với các chỉ số chứng khoán. Vì các nhà quản lý, công ty họ đặt cược mức rủi ro lớn và tất nhiên lợi nhuận thu về cũng sẽ lớn hơn mức trung bình. Vì thế nếu bạn là nhà đầu tư thì nên cân nhắc đến điều này.

Đối với độ lệch chuẩn thấp cũng không chắc chắn rằng sẽ tốt. Điều này còn phụ thuộc vào khoản đầu tư mà bạn đang có và việc bạn có chịu được rủi ro hay không. Đối với những ai có thể chịu được áp lực lớn, có tâm lý thoải mái thì có thể tham gia vào các chiến lược đầu tư có độ biến động cao hơn mức trung bình.

Ví dụ về độ lệch chuẩn

Giả sử chúng ta có các số: 5, 7, 3 và 7, tổng của chúng = 22.

• Lấy 22 chia cho số lượng các số, trong trường hợp này là 4 được 5,5.
• Chúng ta có trung bình là: x̄ = 5,5 và N = 4.

Phương sai sẽ được xác định bằng cách trừ mỗi số cho giá trị trung bình. Theo đó, lần lượt các kết quả là: -0,5, 1,5, -2,5 và 1,5.

Lấy các giá trị đó bình phương lên, kết quả: 0,25, 2,25, 6,25 và 2,25.

Tiếp đến, cộng các giá trị bình phương sau đó chia cho giá trị N trừ 1, bằng 3. => Cho kêt quả phương sai xấp xỉ = 3,67. Căn bậc hai của phương sai có độ lệch chuẩn là khoảng 1.915.

Độ lệch chuẩn và phương sai

Độ lệch chuẩn và phương sai là 2 khái niệm hoàn toàn khác nhau. Đối với phương sai, chúng sẽ được tính bằng cách lấy giá trị trung bình của các quan sát trừ đi giá trị trung bình. Sau đó bình phương từng kết quả và lấy giá trị trung bình. Đối với độ lệch chuẩn, được xác định là căn bậc hai của phương sai.

Phương sai lớn thể hiện sự biến động mạnh trong các giá trị của tập dữ liệu. Nếu phương sai thể hiện giá trị nhỏ nghĩa là bộ số liệu đó có các giá trị gần với giá trị trung bình.

Riêng với độ lệch chuẩn thường dễ hình dung và dễ áp dụng hơn. Độ lệch chuẩn được hiển thị trong một đơn vị đo lường với dữ liệu. Nhờ vào độ lệch chuẩn, các nhà đầu tư, thống kê có thể xác định được dữ liệu có thể hiện chuẩn và chính xác hay không.

Một bất cập của độ lệch chuẩn đó chính là bị ảnh hưởng bởi các điểm ngoại lai và các giá trị âm. Chúng có giả định là phân phối chuẩn và xem tất cả sự không chắc chắn có thể là rủi ro. Ngay cả khi nó có lợi cho nhà đầu tư, điển hình như khi lợi nhuận đạt mức trên trung bình.

Kết luận

Qua những thông tin mà chúng tôi chia sẻ về độ lệch chuẩn là gì và những nội dung liên quan đến khái niệm này. Hy vọng sẽ cung cấp cho bạn đọc được nhiều thông tin hữu ích để bạn có thể áp dụng vào thực tế, công việc có liên quan của mình hiện tại.

Thông tin được biên tập bởi: taichinh24h.com.vn