Đối Xứng Trong Nghệ Thuật (Phần 1) - MyThuatMS

Đối xứng trong nghệ thuật (Phần 1)

Đối xứng trong nghệ thuật (Phần 1)

Mái nhà thờ Sagrada Familia ở Barcelona (Tây Ban Nha), do nghệ sĩ kiến trúc sư Antonio Gaudí (1852-1926) thiết kế, nhìn từ bên trong gian giữa. Nguồn: Wikipedia.

Các ảnh đối xứng là các ảnh có sự giống nhau giữa các phần, tức là chúng tuân thủ nguyên lý lặp đi lặp lại của cái đẹp. Chính bởi vậy mà trong nghệ thuật, và trong cuộc sống hàng ngày, chúng ta gặp rất nhiều ảnh đối xứng đẹp mắt. Ngay các bài thơ, bản nhạc cũng có sự đối xứng. Tuy nhiên phần này sẽ chỉ bàn đến đối xứng trong các nghệ thuật thị giác (visual arts).

* Các phép đối xứng:

Mặt nước phản chiếu tạo ảnh ảnh với đối xứng gương

Trong toán học có định lý sau: Mọi phép biến đổi bảo toàn khoảng cách trong không gian bình thường của chúng ta (tức là không gian Euclid 3 chiều hoặc trên mặt phẳng 2 chiều) đều thuộc một trong bốn loại sau:

1) Phép đối xứng gương (mirror symmetry), hay còn gọi là phép phản chiếu (reflection): trong không gian 3 chiều thì là phản chiếu qua một mặt phẳng nào đó, còn trên mặt phẳng thì là phản chiếu qua một đường thẳng.

2) Phép quay (rotation): trong không gian 3 chiều thì là quay quanh một trục nào đó, còn trên mặt phẳng thì là quay quanh một điểm nào đó, theo một góc nào đó.

Con sao biển có cả đối xứng gương lẫn đối xứng quay một phần năm vòng tròn.

Có những loại sao biển có n chân với n> 5 (thậm chí với n=18), và khi đó nó đối xứng quay theo góc 2p/n.

3) Phép tịnh tiến (translation): dịch chuyển tất cả các điểm đi cùng một khoảng cách theo cùng một hướng nào đó. Như kiểu ánh xạ: τ : (x,y) 7→ (x+T,y) trên mặt phẳng, dịch chuyển các điểm theo hướng của trục x một đoạn có độ dài bằng T.

Đường viền sư tử tại thành cổ Persepolis (Iran)

4) Phép lượn (glide), là kết hợp của một phép đối xứng gương và một phép tịnh tiến theo hướng song song với trục giữa hay mặt giữa của đối xứng gương đó.

Một dải gỗ trang trí, từ invitinghome.com

Định lý trên không quá khó, và có thể dùng làm bài tập thú vị cho học sinh THCS (trường hợp 2 chiều) và THPT (trường hợp 3 chiều).

Nếu chúng ta có một ảnh (hai chiều hoặc ba chiều), và có một trong các phép biến đổi như trên bảo toàn ảnh đó (tức là đổi chỗ các điểm của ảnh cho nhau nhưng biến ảnh vào chính nó), thì ta gọi đó là một phép đối xứng của ảnh. Tất nhiên, ta luôn có một phép đối xứng tầm thường, tức là phép giữ nguyên tất cả các điểm. Nhưng khi nói đến đối xứng, người ta thường hiểu là phép đối xứng không tầm thường. Nếu một ảnh có ít nhất một phép đối xứng không tầm thường, thì được gọi là một ảnh đối xứng. Ảnh nào mà có càng nhiều phép đối xứng, thì ảnh đó càng đối xứng.

Phép tịnh tiến và phép lượn khác phép phản chiếu và phép quay ở chỗ nếu ta cứ lặp đi lặp lại cùng một phép tịnh tiến hay phép lượn lên một điểm ban đầu nào đó, thì điểm đó sẽ chạy dần ra vô cùng. Bởi vậy nếu nói một cách chặt chẽ thì không có một phép tịnh tiến hay phép lượn nào có thể bảo toàn một vật hay một ảnh hữu hạn. Nhưng nếu ta chấp nhận là phép tịnh tiến không cần được thực hiện trên toàn bộ ảnh mà chỉ trên một phần của ảnh, hoặc ta ảnh dung rằng ảnh có thể được trải dài nối tiếp ra đến vô cùng, thì các phép tịnh tiến và phép lượn cũng trở thành phép đối xứng, theo nghĩa mở rộng.

Ảnh 4 khắc họa những con sư tử trên tường thành phố cổ Persepolis ở Iran là một ví dụ về phép đối xứng tịnh tiến theo nghĩa mở rộng: vector tịnh tiến ở đây là vector nối từ mũi một con sư tử đến mũi của con sư tử tiếp theo. Còn ảnh 5 có phép đối xứng lượn theo nghĩa mở rộng.

Các công trình kiến trúc rất hay có đối xứng gương giữa hai bên. Trong ảnh là Mosque (nhà thờ Hồi Giáo) tại Abu Dhabi.

Trong toán học, tập hợp các phép đối xứng của một vật hay một ảnh được gọi là một nhóm (group), bởi ta có thể làm hai phép toán trên đó, là phép nhân (tích của hai phần tử) và phép nghịch đảo. Nghịch đảo của một phép biến đổi đối xứng (bảo toàn ảnh) chính là phép biến đổi ngược lại, tất nhiên cũng bảo toàn ảnh. Còn tích của hai phép biến đổi đối xứng chính là phép "hợp thành" của chúng: đầu tiên ta thực hiện biến đổi theo phép thứ nhất, rồi biến đổi tiếp theo phép thứ hai. Tất nhiên, nếu cả hai phép biến đổi bảo toàn ảnh, thì ảnh vẫn được bảo toàn khi ta thực hiện liên tiếp hai phép biến đổi đó.

Các công trình kiến trúc, đồ vật, ảnh họa và trang trí nghệ thuật có thể được phân loại theo nhóm các đối xứng của chúng. Ví dụ, tháp Phước Duyên ở chùa Thiên Mụ (ảnh 7) có tám mặt, với đáy giống như là một ảnh bát giác đều, và như vậy nhóm đối xứng của nó cũng giống như nhóm đối xứng của một ảnh bát giác đều (nếu ta bỏ qua các chi tiết không đối xứng trên tháp, ví dụ như không phải mặt nào cũng có cửa). Tháp Eiffel ở Paris (ảnh 8) thì có bốn mặt giống nhau, đáy ảnh vuông, nên nhóm đối xứng của nó giống như là nhóm đối xứng của ảnh vuông.

Tháp Phước Duyên ở chùa Thiên Mụ (Huế) có đối xứng theo ảnh bát giác, và kiến trúc xung quanh có đối xứng gương.

Tháp Eiffel ở Paris với 4 mặt như nhau, có nhóm đối xứng D4 giống ảnh vuông.

* Phân loại đa giác theo nhóm đối xứng:

Vào quãng năm 2013, tôi có dành một buổi để tìm hiểu cùng với con gái, lúc đó đang học năm cuối THCS (ở Pháp gọi là "collège"), về các nhóm đối xứng của các đa giác. Kết quả của buổi tìm hiểu và thực hành cùng với giấy và kéo đó được ghi lại trên. Ảnh 9 và được viết lại chi tiết thành một chương trong quyển sách "Các bài giảng về toán cho Mirella". Đây là một hoạt động thực hành toán học đơn giản mà thú vị, các bạn học sinh rất nên làm.

Đầu tiên là xét các tam giác. Chúng có thể có 1 đối xứng (trong trường hợp tam giác không cân, chỉ có phép "để yên" là bảo toàn tam giác), 2 đối xứng (nếu là tam giác cân, ngoài phép để yên còn có phép đối xứng gương), hoặc mấy đối xứng nếu là tam giác đều? Có những người sẽ trả lời là 3, và có những người sẽ trả lời là 4. Câu trả lời chính xác là 6, trong đó có 3 phép đối xứng gương, và 3 phép quay theo các góc 0 độ, 120 độ và 240 độ. (Quay theo góc 0 độ có nghĩa là để yên).

Các đa giác và số các đối xứng của chúng.

Đến lượt tứ giác: nhiều đối xứng nhất là ảnh vuông, với 8 đối xứng (4 đối xứng gương và 4 phép quay), tiếp theo là đến ảnh chữ nhật và ảnh thoi đều có 4 đối xứng. Tiếp theo là các ảnh có 2 đối xứng: ảnh bình hành (với đối xứng quay 180 độ), ảnh thang cân, ảnh mũi tên và ảnh cánh diều (với đối xứng gương). Còn nếu lấy một ảnh tứ giác tùy ý, không có cạnh nào bằng cạnh nào, thì nhóm các đối xứng của nó sẽ là nhóm tầm thường, chỉ có mỗi một phần tử, là phép để yên.

Đến lượt ngũ giác: lại chỉ có 3 trường hợp, tương tự như là với tam giác, chứ không có nhiều trường hợp như là tứ giác.

Khi ngũ giác đều thì có 5×2 = 10 đối xứng, nếu không đều thì hoặc là nhóm đối xứng chỉ có một phần tử (phép để yên) hoặc có hai phần tử (đối xứng gương và phép để yên). Con sao biển trên ảnh 3 có ảnh sao năm cánh đều, và nhóm đối xứng của nó bằng nhóm đối xứng của một ngũ giác đều.

Đến lượt lục giác thì lại có rất nhiều trường hợp khác nhau, rồi đến thất giác thì lại chỉ có 3 trường hợp, và cứ thế. Từ các thí nghiệm này, ta rút ra được một số kết luận toán học sau:

- Ảnh n-giác thì có thể có nhiều nhất là 2n đối xứng, ứng với trường hợp n-giác đều. Nhóm đối xứng trong trường hợp đó gồm n đối xứng gương và n phép quay, và gọi là nhóm nhị diện (dihedral group) Dn. Nếu n-giác không đều, thì nhóm đối xứng của nó là một nhóm con của nhóm Dn, và số các đối xứng là một ước số của 2n.

- Nếu n là số nguyên tố thì chỉ có 3 khả năng xảy ra: hoặc nhóm đối xứng là Dn, hoặc nhóm đó có hai phần tử trong đó phần tử không tầm thường là đối xứng gương, hoặc là nhóm tầm thường (chỉ có mỗi phép để yên).

Khi mà số cạnh của đa giác đều tiến tới vô cùng thì ta được ảnh tròn, là ảnh có nhiều đối xứng nhất trong các ảnh phẳng: vô hạn đối xứng (quay quanh tâm theo góc tùy ý, và đối xứng gương theo đường kính tùy ý).

* Bảy kiểu trang trí đường viền:

Trang trí trên một mái nhà ở Toulouse.

Các trang trí trên các dải mép tường, mép bàn, mép váy, hay những con đường dài và hẹp được gọi chung là trang trí đường viền ("frieze" tiếng Anh, "frise" tiếng Pháp). Có thể ảnh dung một đường viền như là một dải băng D hẹp và dài (coi như dài vô tận cho đơn giản) nằm ngang trên mặt phẳng:

D = R × [−a,a] = {(x,y) ∈ R2 | − a ≤ y ≤ a}

Theo nguyên lý lặp đi lặp lại của cái đẹp, người ta thường trang trí đường viền một cách tuần hoàn, tức là ảnh trang trí trên dải băng D có tính chất bất biến theo một phép tịnh tiến (dịch sang phải hoặc sang trái một khúc có độ dài T nào đó):

τ : (x,y) 7→ (x + T,y)

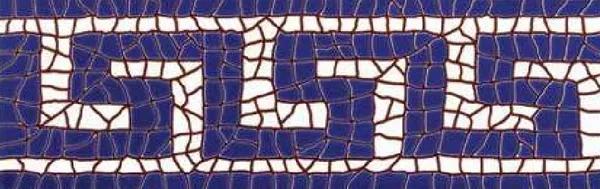Gạch đá hoa trang trí theo một kiểu phương Đông

Ví dụ như trên Ảnh 4, các con sư tử được xếp cách đều nhau trên một đường viền, và dịch một con sư tử sang bên phải một khúc bằng khoảng cách giữa hai cái mũi của hai con sư tử liên tiếp thì được con sư tử tiếp theo.

Các phép tịnh tiến bảo toàn một trang trí đường viền tuần hoàn tạo thành một nhóm tương đương với Z, tức là tập các số nguyên: với mỗi số nguyên k ∈ Z thì ta có một phép "tịnh tiến k bước" bảo toàn ảnh trang trí: τk : (x,y) 7→ (x + kT,y).

Ngoài các phép tịnh tiến ra, thì ảnh trang trí đường viền còn có thể bất biến theo các phép biến đổi khác nữa. Người ta phân loại các kiểu trang trí đường viền tuần hoàn qua nhóm các nhóm đối xứng của chúng. Tổng cộng có đúng bảy kiểu khác nhau:

Kiểu thứ nhất gọi là hop (nhảy lò cò):

Trong kiểu này, chỉ có các phép tịnh tiến là bảo toàn ảnh trang trí. Ảnh đúng như là các vết chân của một bàn chân nhảy lò cò lên phía trước. Các con sư tử trên ảnh 4 là trang trí theo kiểu hop này.

Kiểu thứ hai gọi là step (bước đều):

Trong kiểu này, ngoài phép tịnh tiến, còn phép lượn (glide) cũng bảo toàn ảnh trang trí. Ảnh đúng kiểu này như là đi đều bước bằng hai chân. Ảnh 5 là một ví dụ.

Trang trí trên một hàng rào đá ở Ấn Độ, thế kỷ 16-17

Kiểu thứ ba gọi là sidle (đi ngang):

Trong kiểu này, ngoài phép tịnh tiến, còn phép đối xứng gương theo các trục dọc. Ảnh đúng là hai chân xếp theo hướng dọc rồi đi ngang như con cua, và đối xứng gương ở đây là đối xứng giữa hai chân. Ảnh 10 là một ví dụ.

Kiểu thứ tư gọi là spinning hop (nhảy xoay lò cò):

Trong kiểu này, có những phép quay 180 độ cũng bảo toàn ảnh trang trí. Ảnh 11 là một ví dụ.

Kiểu trang trí “Ngaru” của thổ dân Maori (New Zealand)

Kiểu thứ năm gọi là spinning sidle (đi xoay ngang):

Trong kiểu này, ngoài phép tịnh tiến theo chiều ngang, còn có những phép đối xứng gương theo các trục dọc (đối xứng giữa hai chân) và những phép quay 180 độ. Chú ý rằng tâm của các phép quay 180 độ nằm ngoài các trục đối xứng, và khi kết hợp phép quay 180 độ với phép đối xứng gương thì được phép lượn (glide). Ảnh 12 có thể coi là một ví dụ của kiểu đường viền thứ năm này nếu bỏ qua một vài chi tiết.

Kiểu thứ sáu gọi là jump (nhảy hai chân):

Trong kiểu này, ngoài phép tịnh tiến, còn có phép đối xứng gương theo trục ngang (đối xứng giữa hai chân đặt nằm ngang ở hai bên trục). Ảnh 13 là một ví dụ.

Một góc balcon ở Paris

Kiểu thứ bảy gọi là spinning jump (nhảy xoay hai chân):

Là kiểu cuối cùng. Trong kiểu này, ngoài phép tịnh tiến, còn có những phép đối xứng gương theo cả trục ngang lẫn trục dọc, và những phép quay 180 độ. Ảnh 14 là một ví dụ.

>>> Sự cân bằng các mảng khối (Phần 1)

>>> Nguyên lý hàng lối, cân đối, tự do trong cơ sở tạo hình

>>> Sự dung nhất giữa các phần