Đường Cong Phillips – Wikipedia Tiếng Việt

Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. Mời bạn giúp hoàn thiện bài viết này bằng cách bổ sung chú thích tới các nguồn đáng tin cậy. Các nội dung không có nguồn có thể bị nghi ngờ và xóa bỏ. (tháng 11/2022) (Tìm hiểu cách thức và thời điểm xóa thông báo này)

Đường cong Phillips là một mô hình kinh tế, được đặt tên theo nhà kinh tế học Alban William Phillips – người đưa ra giả thuyết về mối tương quan giữa việc giảm tỉ lệ thất nghiệp và tăng tỉ lệ mức lương trong nền kinh tế.[1][2] Mặc dù chính bản thân Phillips không nêu rõ mối quan hệ liên kết giữa việc làm và lạm phát, nhưng đây là một suy luận nhỏ so với những phát hiện thống kê của ông. Paul Samuelson và Robert Solow đã đưa ra mối liên hệ rõ ràng,[3] và sau đó Milton Friedman[4] và Edmund Phelps[5][6] đã đặt cấu trúc lý thuyết vào đúng vị trí. Khi làm như vậy, Friedman đã dự đoán thành công sự sụp đổ sắp xảy ra của mối tương quan lý thuyết của Phillips.

Mặc dù có một sự đánh đổi ngắn hạn giữa thất nghiệp và lạm phát, nhưng nó đã không được quan sát trong dài hạn.[7] Vào những năm 1967 và 1968, Friedman và Phelps đã khẳng định rằng đường cong Phillips chỉ phù hợp trong ngắn hạn, và về lâu dài, các chính sách lạm phát sẽ không làm giảm tỷ lệ thất nghiệp.[4][5][6][8] Friedman khi đó dự đoán chính xác rằng trong cuộc suy thoái 1973 – 1975, cả lạm phát và thất nghiệp sẽ tăng lên.[8] Đường cong Phillips dài hạn hiện được coi là một đường thẳng đứng với tỷ lệ thất nghiệp tự nhiên, trong đó tỷ lệ lạm phát không ảnh hưởng đến tỷ lệ thất nghiệp. Trong thập niên 2010 độ dốc của đường cong Phillips dường như đã giảm và đã có tranh cãi về tính hữu ích của đường cong Phillips trong việc dự đoán lạm phát.[9] Một nghiên cứu năm 2022 cho thấy độ dốc của đường cong Phillips nhỏ và rất nhỏ ngay cả trong những năm đầu thập niên 1980.[10] Tuy nhiên, đường cong Phillips vẫn là khuôn khổ chính để hiểu và dự báo lạm phát được sử dụng trong các ngân hàng trung ương.[11]

Lịch sử

[sửa | sửa mã nguồn]

Tập tin:Figure 1 from Phillips 1958 paper.png

Alban William Phillips, một nhà kinh tế học sinh ra ở New Zealand, đã viết một bài báo vào năm 1958 có tựa đề về Mối quan hệ giữa tỷ lệ thất nghiệp và tỷ lệ thay đổi của mức lương ở Vương quốc Liên hiệp Anh trong những năm 1861 – 1957, được xuất bản trên tạp chí hàng quý Economica.[1] Trong bài báo, Phillips mô tả cách ông quan sát mối quan hệ nghịch đảo giữa sự thay đổi tiền lương và tỷ lệ thất nghiệp trong giai đoạn được kiểm tra. Các mô hình tương tự cũng được tìm thấy ở các quốc gia khác, và vào năm 1960, Paul Samuelson và Robert Solow đã thực hiện công trình của Phillips và làm rõ mối liên hệ giữa lạm phát và thất nghiệp: khi lạm phát cao, tỷ lệ thất nghiệp thấp và ngược lại.[3]

Trong những năm 1920, nhà kinh tế học người Mỹ Irving Fisher đã lưu ý đến loại quan hệ này của đường cong Phillips. Tuy nhiên, nguyên bản đường cong Phillips là mô tả hành vi của tiền lương.[12]

Những năm sau bài báo năm 1958 của Phillips, nhiều nhà kinh tế ở các nước công nghiệp tiên tiến tin rằng kết quả của ông cho thấy mối quan hệ ổn định vĩnh viễn giữa lạm phát và thất nghiệp. Hàm ý của điều này đối với chính sách của chính phủ là chính phủ có thể kiểm soát thất nghiệp và lạm phát bằng chính sách Keynes. Họ có thể chịu được tỷ lệ lạm phát cao hợp lý vì điều này sẽ dẫn đến tỷ lệ thất nghiệp thấp hơn – nhờ có sự đánh đổi giữa lạm phát và thất nghiệp. Ví dụ, chính sách tiền tệ hoặc chính sách tài khóa có thể được sử dụng để kích thích nền kinh tế, tăng tổng sản phẩm quốc nội và giảm tỷ lệ thất nghiệp. Di chuyển dọc theo đường cong Phillips, điều này sẽ dẫn đến tỷ lệ lạm phát cao hơn, là phí tổn để có được tỷ lệ thất nghiệp thấp hơn. Nhà kinh tế học James Forder lập luận rằng quan điểm này về mặt lịch sử là sai lầm và không chỉ các nhà kinh tế học mà cả các chính phủ cũng đều không chấp nhận quan điểm đó và “huyền thoại đường cong Phillips” là một sáng tác của thập niên 1970.[13]

Kể từ năm 1974, bảy giải thưởng Nobel đã được trao cho các nhà kinh tế học, trong số đó có công trình quan trọng đối với một số biến thể của đường cong Phillips. Một số phê bình đánh giá này dựa trên kinh nghiệm của Mỹ trong thập niên 1970, nơi có thời kì mà tỷ lệ thất nghiệp và tỷ lệ lạm phát cao cùng một lúc. Các tác giả nhận được những giải thưởng đó bao gồm Thomas Sargent, Christopher Sims, Edmund Phelps, Edward Prescott, Robert A. Mundell, Robert E. Lucas, Milton Friedman và F.A. Hayek.[14]

Đình lạm

[sửa | sửa mã nguồn]

Trong thập niên 1970, nhiều quốc gia đã trải qua mức độ lạm phát và tỷ lệ thất nghiệp cao - còn được gọi là tình trạng lạm phát đình trệ. Các lý thuyết dựa trên đường cong Phillips cho thấy rằng điều này không thể xảy ra, và đường cong này đã bị một nhóm các nhà kinh tế học do Milton Friedman đứng đầu phối hợp tấn công. Friedman lập luận rằng mối quan hệ của đường cong Phillips chỉ là một hiện tượng ngắn hạn. Trong đó, ông đã tiếp nối tám năm sau Samuelson và Solow (1960), những người đã viết “tất cả trong thảo luận của chúng ta được diễn giải trong ngắn hạn, đối phó với những gì có thể xảy ra trong vài năm tới. Tuy nhiên, sẽ là sai lầm nếu nghĩ rằng menu trong Hình số 2 của chúng ta liên quan đến giá cả có thể đạt được và hành vi thất nghiệp sẽ được duy trì hình dạng tương tự trong dài hạn. Những gì chúng ta thực hiện trong đường lối chính sách trong vài năm tới có thể khiến nó thay đổi theo một cách thức xác định.”[3] Giống như Samuel và Solow đã lập luận vào 8 năm trước đó, ông cho rằng về lâu dài, người lao động và người sử dụng lao động sẽ tính đến lạm phát, dẫn đến các hợp đồng lao động sẽ tăng lương với mức giá gần lạm phát dự kiến. Sau đó thất nghiệp sẽ bắt đầu tăng trở lại với mức trước đó, nhưng hiện nay với tỷ lệ lạm phát cao hơn. Kết quả này ngụ ý rằng trong dài hạn không có bất kỳ sự đánh đổi nào giữa tỷ lệ lạm phát và tỷ lệ thất nghiệp. Hàm ý này có ý nghĩa đối với các lý do thực tế vì nó ngụ ý rằng các ngân hàng trung ương không nên đặt mục tiêu tỷ lệ thất nghiệp dưới mức tự nhiên.[7]

Một nghiên cứu gần đây cho thấy rằng có sự đánh đổi vừa phải giữa lạm phát và tỷ lệ thất nghiệp ở mức thấp. Công trình nghiên cứu của George Akerlof, William Dickens và George Perry ngụ ý rằng nếu lạm phát giảm từ 2% xuống còn 0%, tỷ lệ thất nghiệp sẽ vĩnh viễn tăng 1,5%.[15] Điều này là do người lao động thường có khả năng chịu cắt giảm lương thực tế cao hơn so với mức lương danh nghĩa. Ví dụ, một công nhân sẽ có nhiều khả năng chấp nhận tăng lương 2% trong khi tỷ lệ lạm phát là 3%, hơn là việc cắt giảm 1% lương khi tỷ lệ lạm phát bằng 0.

Ngày nay

[sửa | sửa mã nguồn]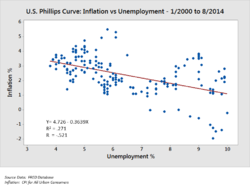

Hầu hết các nhà kinh tế học không còn sử dụng đường cong Phillips ở dạng ban đầu vì nó được chứng minh là quá đơn giản.[16] Điều này có thể thấy được trong một phân tích ngắn gọn về dữ liệu lạm phát và thất nghiệp của Mỹ giai đoạn năm 1953 – 1992. Không có đường cong đơn lẻ nào phù hợp với các dữ liệu, nhưng có 3 tổ hợp thô – 1955-71, 1974-84 và 1985 – 92 – mỗi trong số đó cho thấy một đường dốc tổng thể với độ dốc hướng xuống, nhưng ở ba mức khác nhau với sự thay đổi xảy ra rất đột ngột. Dữ liệu cho các năm 1953 – 1954 và 1972 – 1973 không dễ dàng gộp nhóm và một phân tích chính thức hơn đưa ra tới 5 nhóm/đường cong trong giai đoạn này.[7]

Tuy nhiên, cho tới nay thì các dạng sửa đổi của đường cong Phillips có tính đến các kỳ vọng lạm phát vẫn còn ảnh hưởng. Lý thuyết được đưa ra dưới nhiều tên gọi, với một số thay đổi trong các chi tiết của nó, nhưng tất cả các phiên bản hiện đại đều tách biệt giữa tác động ngắn hạn và dài hạn đối với tỷ lệ thất nghiệp. Các mô hình đường cong Phillips hiện đại bao gồm cả đường cong Phillips ngắn hạn và đường cong Phillips dài hạn. Điều này là do trong ngắn hạn, nhìn chung có mối quan hệ nghịch đảo giữa tỷ lệ lạm phát và tỷ lệ thất nghiệp; như được minh họa trong đường cong Phillips ngắn hạn dốc xuống. Trong dài hạn, mối quan hệ đó bị phá vỡ và cuối cùng nền kinh tế trở lại tỷ lệ thất nghiệp tự nhiên bất kể tỷ lệ lạm phát nào.[17]

Edmund Phelps và Milton Friedman lập luận rằng “đường cong Phillips ngắn hạn” còn được gọi là “đường cong Phillips kỳ vọng – tăng cường” vì nó dịch chuyển lên khi kỳ vọng về lạm phát tăng lên. Trong dài hạn, điều này có nghĩa rằng chính sách tiền tệ không thể tác động đến tỷ lệ thất nghiệp, nó sẽ điều chỉnh trở lại “tỷ lệ tự nhiên” của mình, còn được gọi là “NAIRU”. Trong sách giáo khoa phổ biến của Blanchard đưa ra phần trình bày về đường cong Phillips kỳ vọng – tăng cường.[18]

Một phương trình giống như đường cong Phillips kỳ vọng – tăng cường cũng xuất hiện trong nhiều mô hình cân bằng tổng thể ngẫu nhiên động Keynes mới gần đây. Như Keynes đã đề cập: “tuy nhiên, chính phủ cần phải nhớ rằng ngay cả khi thuế không có tính chất ngăn cấm thì nó có thể vẫn là không có lợi, và việc áp thuế ở mức vừa phải thay vì mức tột cùng sẽ mang lại lợi ích lớn nhất”.[19] Trong các mô hình kinh tế vĩ mô với giá cả cố định, có mối quan hệ tỷ lệ thuận giữa tỷ lệ lạm phát và mức độ nhu cầu, và do đó có mối quan hệ tỷ lệ nghịch giữa tỷ lệ lạm phát và tỷ lệ thất nghiệp. Mối quan hệ này thường gọi là “đường cong Phillips Keynes mới”. Giống như đường cong Phillips kỳ vọng – tăng cường, đường cong Phillips Keynes mới có nghĩa là lạm phát cao có thể giảm tỷ lệ thất nghiệp tạm thời nhưng không thể giảm vĩnh viễn. Hai bài báo có sức ảnh hưởng kết hợp đường cong Phillips Keynes mới là của Clarida, Galí và Gertler (1999),[20] và Blanchard và Galí (2007).[21]

Toán học

[sửa | sửa mã nguồn]

Có ít nhất hai dẫn xuất toán học khác nhau của đường cong Phillips. Đầu tiên, phiên bản truyền thống hoặc phiên bản Keynes. Sau đó, phiên bản cổ điển mới liên quan đến Robert E.Lucas Jr..

Đường cong Phillips truyền thống

[sửa | sửa mã nguồn]

Tài liệu về đường cong Phillips ban đầu không dựa trên việc áp dụng lý thuyết kinh tế một cách đơn giản. Thay vào đó, nó dựa trên những khái quát hóa theo kinh nghiệm. Sau đó, các nhà kinh tế đã cố gắng phát triển các lý thuyết phù hợp với dữ liệu.

Xác định tiền lương

[sửa | sửa mã nguồn]

Đường cong Phillips truyền thống bắt đầu từ đường cong Phillips tiền lương, thuộc loại được mô tả bởi chính Phillips. Điều này mô tả tốc độ tăng trưởng của tiền lương (gW). Từ đây trở đi, toán tử g tương đương với “tỷ lệ phần trăm tăng trưởng của” biến theo sau:

g W = g W T − f ( U ) {\displaystyle gW=gW^{T}-f(U)}

“Tỷ lệ tiền lương” (W) là viết tắt cho tổng chi phí tiền lương cho mỗi nhân viên sản xuất, bao gồm các khoản phúc lợi và thuế thu nhập cá nhân. Trọng tâm chỉ là tiền lương của nhân viên sản xuất bởi vì (như được thảo luận dưới đây) các chi phí này rất quan trọng đối với các quyết định về giá của các doanh nghiệp.

Phương trình này cho chúng ta biết sự tăng trưởng của tiền lương tăng theo xu hướng tỷ lệ tăng trưởng tiền lương (được biểu thị bằng chỉ số trên T) và giảm theo tỷ lệ thất nghiệp (U). Hàm f được giả thiết là tăng đơn điệu theo U, sao cho sự giảm bớt của sự gia tăng tiền lương vì thất nghiệp được thể hiện bằng dấu âm trong phương trình trên.

Có một số vấn đề có thể xảy ra đằng sau phương trình này. Một vấn đề chính là tiền lương được ấn định bởi các cuộc đàm phán song phương dưới sự độc quyền song phương một phần: khi tỷ lệ thất nghiệp tăng lên, khi tất cả những thứ khác giữ nguyên (ceteris paribus) thì khả năng thương lượng của người lao động giảm xuống, do đó người lao động ít có khả năng tăng tiền lương khi đối mặt với sự phản đối của người sử dụng lao động.

Trong thập niên 1970, câu chuyện này đã phải sửa đổi, vì người lao động cố gắng theo kịp lạm phát (như nhà kinh tế học Abba Lerner đề xuất vào thập niên 1940). Kể từ thập niên 1970, phương trình này đã được thay đổi để thêm vào vai trò của các kỳ vọng lạm phát (hoặc tỷ lệ lạm phát kỳ vọng, gPex). Điều này tạo ra các đường cong Phillips lương kỳ vọng – tăng cường.

g W = g W T − f ( U ) + λ g P ex . {\displaystyle gW=gW^{T}-f(U)+\lambda gP^{\text{ex}}.}

Việc đưa các kỳ vọng lạm phát vào phương trình ngụ ý rằng lạm phát thực tế có thể phản hồi thành các kỳ vọng lạm phát và do đó có thể gây ra lạm phát thêm nữa. Nhà kinh tế học James Tobin gọi thuật ngữ cuối cùng này là “quán tính lạm phát”, vì trong giai đoạn hiện tại thì sự tồn tại của lạm phát thể hiện cho xung lực lạm phát sót lại từ quá khứ.

Nó cũng bao hàm nhiều hơn là các kỳ vọng, bao gồm cả vòng xoáy giá cả - tiền lương. Trong vòng xoáy này, những người sử dụng lao động cố gắng bảo vệ lợi nhuận bằng cách tăng giá của họ và người lao động của họ cố gắng bắt kịp lạm phát để bảo vệ mức lương thực tế của họ. Quá trình này có thể tự nuôi sống chính nó, trở thành một lời tiên tri tự hoàn thành.

Tham số λ (được cho là không đổi trong bất kỳ khoảng thời gian nào) thể hiện mức độ mà người lao động có thể thu được mức gia tăng tiền lương để bắt kịp với lạm phát dự kiến, ngăn chặn sự sụt giảm tiền lương thực tế dự kiến. Người ta thường giả định rằng tham số này bằng 1 trong dài hạn.

Ngoài ra, hàm số f() đã được sửa đổi để được đưa ra ý tưởng về tỷ lệ thất nghiệp không làm lạm phát tăng tốc (NAIRU) hoặc đôi khi được gọi là tỷ lệ thất nghiệp “tự nhiên” hay tỷ lệ thất nghiệp ngưỡng lạm phát.

g W = g W T − f ( U − U ∗ ) + λ g P ex . {\displaystyle gW=gW^{T}-f(U-U^{*})+\lambda gP^{\text{ex}}.}

(1)

Ở đây, U* là NAIRU. Như thảo luận dưới đây, nếu U < U*, lạm phát có xu hướng tăng nhanh. Tương tự, nếu U > U*, lạm phát có hướng chậm lại. Giả thiết rằng f(0) = 0, do đó khi U = U*, hạng tử f có thể bỏ ra khỏi phương trình.

Trong phương trình (1), vai trò của gWT và gPex dường như là dư thừa, do có vai trò giống nhau. Tuy nhiên, giả sử rằng λ bằng 1, có thể thấy rằng nó không còn dư thừa. Nếu xu hướng của tốc độ tăng trưởng tiền lương bằng 0, thì trường hợp U bằng U* ngụ ý rằng gW bằng lạm phát kỳ vọng. Nghĩa là, mức lương thực tế dự kiến là không đổi.

Tuy nhiên, trong bất kỳ nền kinh tế hợp lý nào, việc có mức lương thực tế kỳ vọng không đổi chỉ có thể phù hợp với mức lương thực tế không đổi trong thời gian dài. Điều này không phù hợp với những gì kinh tế ở Mỹ hoặc bất kỳ quốc gia công nghiệp lớn nào khác đã trải qua. Mặc dù tiền lương thực tế không tăng nhiều trong những năm gần đây, nhưng đã có những mức tăng quan trọng trong nhiều thập kỷ.

Một phương án khác là giả định rằng xu hướng của tốc độ tăng trưởng tiền lương tương đương với xu hướng của tốc độ tăng trưởng năng suất lao động trung bình (Z). Khi đó là:

g W T = g Z T . {\displaystyle gW^{T}=gZ^{T}.}

(2)

Theo giả định (2), khi U bằng U* và λ bằng 1, tiền lương thực tế kỳ vọng sẽ tăng theo năng suất lao động. Điều này sẽ phù hợp với một nền kinh tế trong đó tiền lương thực tế tăng theo năng suất lao động. Sự chệch hướng của xu hướng tiền lương thực tế so với năng suất lao động có thể được giải thích bằng cách tham chiếu đến các biến khác trong mô hình.

Quyết định về giá

[sửa | sửa mã nguồn]

Tiếp theo, về hành vi giá cả. Giả định tiêu chuẩn là thị trường cạnh tranh không hoàn hảo, trong đó hầu hết các doanh nghiệp có quyền định giá. Vì vậy, mô hình giả định rằng doanh nghiệp trung bình đặt đơn giá (P) như một khoản cộng dồn lãi vào giá vốn (M) so với chi phí lao động đơn vị trong sản xuất được tính ở tỷ lệ sử dụng công suất tiêu chuẩn (chẳng hạn như ở mức sử dụng nhà máy và thiết bị là 90%) và sau đó cộng vào chi phí nguyên vật liệu đơn vị.

Việc tiêu chuẩn hóa liên quan đến việc bỏ qua những sai lệch sau này so với xu hướng của năng suất lao động. Ví dụ, giả sử rằng sự tăng năng suất lao động giống như tăng trưởng trong xu hướng và năng suất hiện tại bằng giá trị xu hướng của nó.

gZ = gZT and Z = ZT

Khoản cộng dồn lãi vào giá vốn phản ánh cả mức độ quyền lực thị trường của doanh nghiệp và mức độ phải trả chi phí chung. Nói cách khác, khi tất cả những thứ khác đều tương đương, M tăng theo khả năng định giá của doanh nghiệp hoặc với sự gia tăng của chi phí chung so với tổng chi phí. Vì thế, việc định giá tuân theo phương trình sau:

P = M × (chi phí lao động đơn vị) + (chi phí nguyên vật liệu đơn vị) = M × (tổng chi phí việc lao động sản xuất)/(sản lượng đầu ra) + UMC.

UMC là chi phí nguyên vật liệu đơn vị (= tổng chi phí nguyên vật liệu chia cho tổng sản lượng). Vì vậy, phương trình có thể được viết lại như sau:

P = M × (chi phí sử dụng lao động sản xuất trên mỗi công nhân)/(sản lượng trên mỗi lao động sản xuất) + UMC.

Phương trình có thể được phát biểu lại là:

P = M×(tiền lương trung bình)/(năng suất lao động sản xuất) + UMC = M×(W/Z) + UMC.

Bây giờ, giả sử rằng giá cả trung bình/cộng dồn lãi vào giá vốn (M) và UMC đều không đổi. Mặt khác, năng suất lao động tăng lên như trước đây. Do đó, phương trình xác định tỷ lệ lạm phát giá (gP) là:

gP = gW − gZT.

Giá cả

[sửa | sửa mã nguồn]

Sau đó, kết hợp với đường cong Phillips lương (phương trình 1) và giả định được đưa ra ở trên về hành vi xu hướng của tiền lương (phương trình 2), phương trình giá – lạm phát này cho chúng ta một đường cong Phillips giá kỳ vọng – tăng cường đơn giản.

gP = −f(U − U*) + λ·gPex

Một số giả định cho rằng chúng ta có thể chỉ cần thêm gUMC, tốc độ tăng trưởng của UMC, để thể hiện vai trò của sốc cung (loại đã diễn ra tại Mỹ trong thập niên 1970). Điều này tạo ra một đường cong Phillips ngắn hạn tiêu chuẩn:

gP = −f(U − U*) + λ·gPex + gUMC

Nhà kinh tế học Robert J. Gordon gọi đây là “Mô hình Tam giác” vì nó giải thích hành vi lạm phát ngắn hạn theo ba yếu tố: lạm phát do cầu kéo (do tỷ lệ thất nghiệp thấp), lạm phát do sốc cung (gUMC) và các kỳ vọng lạm phát hay lạm phát quán tính.

Trong dài hạn, giả định rằng lạm phát kỳ vọng bắt kịp và bằng với lạm phát thực tế để gP = gPex. Điều này thể hiện trạng thái cân bằng dài hạn của việc điều chỉnh các kỳ vọng. Một phần của sự điều chỉnh này có thể liên quan đến sự thích ứng của các kỳ vọng với trải nghiệm lạm phát thực tế. Phần khác có thể liên quan đến các dự đoán của những người trong nền kinh tế dựa trên các bằng chứng khác (Ý tưởng sau đã cho chúng ta khái niệm về cái gọi là các kỳ vọng hợp lý).

Điểm cân bằng kỳ vọng cho chúng ta đường cong Phillips dài hạn. Đầu tiên, với λ nhỏ hơn 1:

gP = [1/(1 − λ)]·(−f(U − U*) + gUMC)

Đây là một phiên bản dốc hơn của đường cong Phillips ngắn hạn ở trên. Lạm phát tăng khi tỷ lệ thất nghiệp giảm, trong khi mối liên hệ này mạnh mẽ hơn. Có nghĩa là, tỷ lệ thất nghiệp thấp (nhỏ hơn U*) sẽ gắn với tỷ lệ lạm phát trong dài hạn cao hơn trong ngắn hạn. Điều này xảy ra bởi vì tình hình lạm phát thực tế cao hơn được thấy trong ngắn hạn sẽ phản hồi làm tăng các kỳ vọng lạm phát, từ đó làm tăng tỷ lệ lạm phát hơn nữa. Tương tự, ở tỷ lệ thất nghiệp cao (lớn hơn U*) dẫn đến các tỷ lệ lạm phát thấp. Tới lượt mình, chúng khuyến khích các kỳ vọng lạm phát thấp hơn, do đó, lạm phát tiếp tục giảm xuống.

Logic này đi xa hơn nếu λ bằng 1, tức là, nếu người lao động có thể bảo vệ hoàn toàn tiền lương của họ khỏi lạm phát kỳ vọng, ngay cả trong ngắn hạn. Bây giờ, phương trình Mô hình Tam giác trở thành:

- f(U − U*) = gUMC

Nếu chúng ta tiếp tục giả định (có vẻ hợp lý) rằng không có sốc cung dài hạn, điều này có thể được đơn giản hóa thành:

−f(U − U*) = 0 ngụ ý rằng U = U*.

Tất cả các giả định ngụ ý rằng trong dài hạn, chỉ có một tỷ lệ thất nghiệp có thể xảy ra, U* tại bất cứ thời điểm nào. Tính duy nhất này giải thích tại sao một số người gọi tỷ lệ thất nghiệp này là “tự nhiên”.

Để thực sự hiểu và đánh giá tính duy nhất của U*, cần có một mô hình tinh vi và thực tế hơn. Ví dụ, chúng ta có thể đưa ra ý tưởng rằng những người lao động trong các lĩnh vực khác nhau thúc đẩy tăng lương danh nghĩa tương tự như những người lao động trong các lĩnh vực khác. Hoặc chúng ta có thể làm cho mô hình thậm chí còn thực tế hơn. Một điểm quan trọng cần xem xét là sự xác định của mức cộng gộp lãi vào vốn, M.

Phiên bản cổ điển mới

[sửa | sửa mã nguồn]

Phương trình đường cong Phillips có thể được suy ra từ hàm tổng cung Lucas (ngắn hạn). Cách tiếp cận của Lucas rất khác so với cách tiếp cận truyền thống. Thay vì bắt đầu với dữ liệu thực nghiệm, ông bắt đầu với mô hình kinh tế cổ điển tuân theo các nguyên tắc kinh tế rất đơn giản.

Bắt đầu với hàm tổng cung:

Y = Y n + a ( P − P e ) {\displaystyle Y=Y_{n}+a(P-P_{e})\,}

Trong đó, Y là giá trị log của sản lượng thực tế, Y n {\displaystyle Y_{n}} là giá trị log của mức sản lượng tự nhiên, a {\displaystyle a} là hằng số dương, P {\displaystyle P} là giá trị log của mức giá thực tế, và P e {\displaystyle P_{e}} là giá trị log của mức giá dự kiến. Lucas giả định rằng Y n {\displaystyle Y_{n}} có một giá trị duy nhất.

Lưu ý rằng phương trình này chỉ ra rằng khi các kỳ vọng về lạm phát trong tương lai (hay nói đúng hơn là mức giá trong tương lai) là hoàn toàn chính xác, thì hạng tử cuối cùng có thể loại bỏ, do đó sản lượng thực tế bằng với mức được gọi là “tự nhiên” của GDP thực. Điều này có nghĩa là trong đường cong tổng cung Lucas, lý do duy nhất khiến GDP thực tế chệch khỏi GDP tiềm năng – và tỷ lệ thất nghiệp thực tế chệch khỏi tỷ lệ thất nghiệp “tự nhiên” – là do các kỳ vọng không chính xác về những gì sẽ xảy ra với giá cả tương lai (Ý tưởng này đã được trình bày trong Keynes, Lý thuyết tổng quát, chương 20 phần III đoạn 4).

Điều này khác với các quan điểm khác của đường cong Phillips, trong đó việc không đạt được mức sản lượng “tự nhiên” có thể là do sự không hoàn hảo hoặc không hoàn chỉnh của thị trường, giá cả cứng nhắc và các yếu tố tương tự. Trong các quan điểm phi-Lucas, các kỳ vọng không chính xác có thể góp phần vào sự thất bại của tổng cầu, nhưng đó không phải là nguyên nhân duy nhất. Đối với những người theo chủ nghĩa “Cổ điển mới” của Lucas, thị trường được cho là hoàn hảo và luôn đạt được trạng thái cân bằng (với các kỳ vọng lạm phát).

Phương trình được sắp xếp lại thành:

P = P e + Y − Y n a {\displaystyle P=P_{e}+{\frac {Y-Y_{n}}{a}}}

Tiếp theo, chúng ta thêm các sốc ngoại sinh bất ngờ với cung toàn cầu v {\displaystyle v} :

P = P e + Y − Y n a + v {\displaystyle P=P_{e}+{\frac {Y-Y_{n}}{a}}+v}

Trừ các mức giá của năm trước P − 1 {\displaystyle P_{-1}} sẽ cho chúng ta tỷ lệ lạm phát, bởi vì:

P − P − 1   ≈ π {\displaystyle P-P_{-1}\ \approx \pi }

Và

P e − P − 1   ≈ π e {\displaystyle P_{e}-P_{-1}\ \approx \pi _{e}}

Trong đó, π {\displaystyle \pi } và π e {\displaystyle \pi _{e}} lần lượt là lạm phát và lạm phát kỳ vọng.

Ngoài ra còn có mối quan hệ nghịch biến giữa sản lượng và tỷ lệ thất nghiệp (như được thể hiện bởi định luật Okun). Do đó, sử dụng:

Y − Y n a = − b ( U − U n ) {\displaystyle {\frac {Y-Y_{n}}{a}}=-b(U-U_{n})}

Trong đó b {\displaystyle b} là hằng số dương, U {\displaystyle U} là tỷ lệ thất nghiệp và U n {\displaystyle U_{n}} là tỷ lệ thất nghiệp tự nhiên hoặc NAIRU, chúng ta đến với dạng cuối cùng của đường cong Phillips ngắn hạn:

π = π e − b ( U − U n ) + v . {\displaystyle \pi =\pi _{e}-b(U-U_{n})+v.}

Phương trình này, vẽ biểu đồ tỷ lệ lạm phát π {\displaystyle \pi } so với tỷ lệ thất nghiệp U {\displaystyle U} tạo ra đường cong dốc xuống trong biểu đồ đặc trưng cho đường cong Phillips.

Phiên bản mới Keynes

[sửa | sửa mã nguồn]

Đường cong Phillips mới Keynes ban đầu được Robert đưa vào sử dụng vào năm 1995,[22] và kể từ đó được sử dụng trong hầu hết các mô hình DSGE mới hiện đại như một mô hình của Clarida, Galí và Gertler (2000).[23][24]

π t = β E t [ π t + 1 ] + κ y t {\displaystyle \pi _{t}=\beta E_{t}[\pi _{t+1}]+\kappa y_{t}}

Trong đó

κ = α [ 1 − ( 1 − α ) β ] ϕ 1 − α . {\displaystyle \kappa ={\frac {\alpha [1-(1-\alpha )\beta ]\phi }{1-\alpha }}.}

Các kỳ vọng hiện tại về lạm phát của kỳ tiếp theo được kết hợp thành β E t [ π t + 1 ] {\displaystyle \beta E_{t}[\pi _{t+1}]} .

NAIRU và các kỳ vọng hợp lý

[sửa | sửa mã nguồn]

Trong thập niên 1970, các lý thuyết mới, như kỳ vọng hợp lý và NAIRU (tỷ lệ thất nghiệp tự nhiên) đã phát sinh để giải thích làm thế nào lạm phát đình trệ có thể xảy ra. Lý thuyết thứ hai, còn được gọi là “tỷ lệ thất nghiệp tự nhiên”, tách biệt giữa đường cong Phillips “ngắn hạn” và “dài hạn”. Đường cong Phillips ngắn hạn trông giống như đường cong Phillips bình thường nhưng thay đổi trong dài hạn khi kỳ vọng thay đổi. Trong dài hạn, chỉ có một tỷ lệ thất nghiệp duy nhất (NAIRU hoặc tỷ lệ “tự nhiên”) phù hợp với tỷ lệ lạm phát ổn định. Do đó, đường cong Phillips dài hạn là một đường thẳng đứng, vì vậy không có sự đánh đổi giữa lạm phát và thất nghiệp. Milton Friedman năm 1976 và Edmund Phelps năm 2006 đã giành giải thưởng Nobel trong kinh tế học một phần là do công trình này.[25][26] Tuy nhiên, lập cứ về các kỳ vọng trên thực tế đã được hiểu rất rộng rãi (mặc dù không chính thức) trước khi Friedman và Phelps nghiên cứu về nó.[27]

Trong biểu đồ, đường cong Phillips dài hạn là đường thẳng đứng màu đỏ. Lý thuyết NAIRU nói rằng khi thất nghiệp ở mức được xác định bởi đường này, lạm phát sẽ ổn định. Tuy nhiên, trong ngắn hạn các nhà hoạch định chính sách sẽ phải đối mặt với sự đánh đổi giữa lạm phát và tỷ lệ thất nghiệp – được đánh dấu bởi “đường cong Phillips ngắn hạn ban đầu” trong đồ thị. Do đó, các nhà hoạch định chính sách có thể giảm tỷ lệ thất nghiệp tạm thời, chuyển từ điểm A sang điểm B thông qua chính sách mở rộng. Tuy nhiên, theo NAIRU, việc khai thác sự đánh đổi ngắn hạn này sẽ làm tăng các kỳ vọng lạm phát, dịch chuyển đường cong ngắn hạn sang bên phải thành “đường cong Phillips ngắn hạn mới” và di chuyển điểm cân bằng từ B đến C. Do đó tỷ lệ thất nghiệp giảm xuống dưới “Tỷ lệ Tự nhiên” sẽ chỉ là tạm thời và chỉ dẫn đến lạm phát cao hơn trong dài hạn.

Vì đường cong ngắn hạn chuyển ra ngoài do nỗ lực giảm tỷ lệ thất nghiệp, chính sách mở rộng cuối cùng làm xấu đi sự đánh đổi có thể khai thác giữa thất nghiệp và lạm phát. Nghĩa là, điều đó dẫn đến lạm phát cao hơn ở mỗi tỷ lệ thất nghiệp ngắn hạn. Tên “NAIRU” phát sinh bởi vì với tỷ lệ thất nghiệp thực tế thấp hơn nó, lạm phát tăng nhanh, trong khi với tỷ lệ thất nghiệp ở trên nó, lạm phát giảm xuống. Với tỷ lệ thực tế bằng với nó, lạm phát ổn định, không tăng cũng không giảm. Một ứng dụng thực tế của mô hình này là để giải thích tình trạng đình lạm, điều làm nhiễu đường cong Phillips truyền thống.

Lý thuyết kỳ vọng hợp lý nói rằng các kỳ vọng lạm phát bằng với những gì thực sự đã xảy ra, với một số sai sót nhỏ và tạm thời. Ngược lại, điều này cho thấy rằng thời gian ngắn hạn quá ngắn đến mức nó không tồn tại, bất kỳ nỗ lực nào để giảm tỷ lệ thất nghiệp xuống dưới NAIRU, chẳng hạn, sẽ ngay lập tức khiến các kỳ vọng lạm phát tăng lên và do đó có nghĩa rằng chính sách sẽ thất bại. Tỷ lệ thất nghiệp sẽ không bao giờ lệch khỏi NAIRU ngoại trừ do những sai lầm ngẫu nhiên và nhất thời trong việc phát triển các kỳ vọng về tỷ lệ lạm phát trong tương lai. Trong quan điểm này, bất kỳ sai lệch nào của tỷ lệ thất nghiệp thực tế từ NAIRU là ảo ảnh.

Tuy nhiên, trong thập niên 1990 ở Mỹ, ngày càng rõ ràng rằng NAIRU không có trạng thái cân bằng duy nhất và có thể thay đổi theo những cách không thể đoán trước. Vào cuối thập niên 1990, tỷ lệ thất nghiệp thực tế giảm xuống dưới 4% lực lượng lao động, thấp hơn nhiều so với hầu hết các ước tính của NAIRU. Nhưng lạm phát vẫn giữ ở mức rất vừa phải thay vì tăng lên. Vì vậy, giống như đường cong Phillips, NAIRU cũng trở thành một chủ đề tranh luận.

Hơn nữa, khái niệm về kỳ vọng hợp lý đã trở thành đối tượng bị nghi ngờ khi rõ ràng rằng giả định chính của các mô hình dựa trên nó là tồn tại một trạng thái cân bằng độc nhất (duy nhất) trong nền kinh tế được thiết lập trước thời hạn, được xác định độc lập với các điều kiện của cầu. Kinh nghiệm của thập niên 1990 cho thấy rằng giả định này không thể được duy trì.

Các câu hỏi lý thuyết

[sửa | sửa mã nguồn]

Đường cong Phillips bắt đầu như một quan sát thực nghiệm để tìm kiếm một lời giải thích lý thuyết. Cụ thể, đường cong Phillips đã cố gắng xác định xem liệu mối liên hệ giữa lạm phát – thất nghiệp là quan hệ nhân quả hay chỉ đơn giản là tương quan. Có một số giải thích chính về tính hợp thức của đường cong Phillips ngắn hạn.

Đối với Milton Friedman, có mối tương quan ngắn hạn giữa sốc lạm phát và việc làm. Khi lạm phát bất ngờ xảy ra, người lao động bị đánh lừa để chấp nhận trả lương thấp hơn vì họ không thể thấy mức lương thực tế giảm ngay lập tức. Các doanh nghiệp thuê họ bởi vì họ thấy lạm phát cho phép lợi nhuận cao hơn với mức lương danh nghĩa nhất định. Đây là sự di chuyển dọc theo đường cong Phillips khi thay đổi A. Cuối cùng, những người lao động phát hiện ra rằng tiền lương thực tế đã giảm, vì vậy họ thúc đẩy mức lương cao hơn. Điều này làm cho đường cong Phillips dịch chuyển lên trên và sang phải, như với B. Một số nghiên cứu nhấn mạnh rằng một số giả định ngầm và nghiêm trọng thực sự nằm trên nền tảng đường cong Phillips Friedmanian. Sự bất cân xứng thông tin này và một mô hình đặc biệt về tính linh hoạt của giá cả và tiền lương đều cần thiết nếu người ta muốn duy trì cơ chế mà Friedman nói. Tuy nhiên, như đã lập luận, những giả định này vẫn hoàn toàn chấp nhận và lý thuyết của Friedman vẫn không có căn cứ.[28]

Các nhà kinh tế như Edmund Phelps bác bỏ lý thuyết này vì nó ngụ ý rằng người lao động mắc chứng ảo tưởng về tiền bạc. Theo họ, những người lao động có lý trí sẽ chỉ phản ứng với tiền lương thực tế, nghĩa là tiền lương được điều chỉnh theo lạm phát. Tuy nhiên, một trong những đặc điểm của một nền kinh tế công nghiệp hiện đại là người lao động không gặp phải người sử dụng lao động của họ trong một thị trường hoàn hảo và nguyên tử hóa. Họ hoạt động trong sự kết hợp phức tạp của các thị trường không hoàn hảo, các công ty độc quyền, các tổ chức độc quyền, công đoàn lao động và các tổ chức khác. Trong nhiều trường hợp, họ có thể thiếu khả năng thương lượng để hành động theo mong đợi của họ, bất kể họ có lý trí như thế nào, hay nhận thức của họ đến đâu, bất kể họ có ảo tưởng về tiền bạc như thế nào. Không phải lạm phát cao gây ra thất nghiệp thấp (như lý thuyết của Milton Friedman) mà ngược lại: tỷ lệ thất nghiệp thấp làm tăng khả năng thương lượng của người lao động, cho phép họ thúc đẩy thành công mức lương danh nghĩa cao hơn. Để bảo vệ lợi ích, những người sử dụng lao động tăng giá.

Tương tự, lạm phát vốn có không chỉ đơn giản là vấn đề chủ quan của “lạm phát kỳ vọng” mà còn phản ánh thực tế rằng lạm phát cao có thể tạo ra động lực và tiếp tục vượt qua thời điểm bắt đầu, do vòng xoáy giá cả/ tiền lương khách quan.

Tuy nhiên, các nhà kinh tế học khác, như Jeffrey Herbener, cho rằng giá cả là do thị trường quyết định và các công ty cạnh tranh không thể chỉ đơn giản là tăng giá. họ bác bỏ hoàn toàn đường cong Phillips, tóm lại rằng ảnh hưởng của thất nghiệp chỉ là một phần nhỏ trong bức tranh lạm phát lớn hơn nhiều, điều đó bao gồm giá nguyên vật liệu thô, hàng hóa trung gian, chi phí huy động vốn, năng suất lao động, đất đai và các yếu tố khác.

Mô hình tam giác của Gordon

[sửa | sửa mã nguồn]

Robert J. Gordon từ Đại học Northwestern đã phân tích đường cong Phillips để tạo ra cái mà ông gọi là mô hình tam giác, trong đó tỷ lệ lạm phát thực tế được xác định bởi tổng số của:

1. Lạm phát đường cong Phillips ngắn hạn;
2. Lạm phát chi phí đẩy hoặc sốc cung; và
3. Lạm phát nội tại

Lạm phát nội tại phản ánh các kỳ vọng lạm phát và vòng xoáy giá/tiền lương. Các sốc cung và thay đổi lạm phát nội tại là các yếu tố chính dịch chuyển đường cong Phillips ngắn hạn và thay đổi sự đánh đổi. Theo lý thuyết này, không chỉ các kỳ vọng lạm phát có thể gây ra đình lạm. Ví dụ, việc giá dầu leo thang trong thập niên 1970 có thể dẫn đến kết quả này.

Những thay đổi trong lạm phát nội tại tuân theo logic điều chỉnh từng phần đứng phía sau hầu hết các lý thuyết của NAIRU:

1. Tỷ lệ thất nghiệp thấp khuyến khích lạm phát cao, như với đường cong Phillips đơn giản. Nhưng nếu tỷ lệ thất nghiệp vẫn ở mức thấp và lạm phát vẫn ở mức cao trong một thời gian dài, như vào cuối thập niên 1960 ở Mỹ, thì cả các kỳ vọng lạm phát và vòng xoáy giá/tiền lương đều tăng tốc. Điều này làm dịch chuyển đường cong Phillips ngắn hạn lên trên và sang phải, do đó, lạm phát được nhìn thấy nhiều hơn ở bất kỳ tỷ lệ thất nghiệp nào (Điều này là với sự thay đổi B trong sơ đồ).
2. Tỷ lệ thất nghiệp cao khuyến khích lạm phát thấp, một lần nữa như với đường cong Phillips đơn giản. Nhưng nếu tỷ lệ thất nghiệp vẫn ở mức cao và lạm phát vẫn ở mức thấp trong một thời gian dài, như vào đầu thập niên 1980 ở Mỹ, thì cả các kỳ vọng lạm phát và vòng xoáy giá cả/mức lương đều giảm tốc. Điều này làm dịch chuyển đường cong Phillips ngắn hạn xuống dưới và sang trái, do đó tỷ lệ lạm phát thấp hơn ở mỗi tỷ lệ thất nghiệp.

Ở giữa hai đường này là NAIRU, nơi đường cong Phillips không có xu hướng nội tại nào để thay đổi, do đó tỷ lệ lạm phát ổn định. Tuy nhiên, dường như có một khoảng ở giữa giữa "cao" và "thấp" trong đó lạm phát nội tại vẫn ổn định. Các kết thúc của "khoảng các tỷ lệ thất nghiệp tự nhiên” này thay đổi theo thời gian.

Lý luận của trường phái kinh tế học vĩ mô tổng hợp

[sửa | sửa mã nguồn]

Kinh tế Mỹ thập niên 1960 có hiện tượng tỷ lệ lạm phát khá cao mặc dù tốc độ tăng trưởng GDP cũng cao. Để giải thích hiện tượng đó, các nhà kinh tế của trường phái kinh tế học vĩ mô tổng hợp đã sử dụng kết quả nghiên cứu của Phillips và dựng lên đường cong Phillips dốc xuống phía phải trên một đồ thị hai chiều với trục hoành là các mức tỷ lệ thất nghiệp và trục tung là các mức tỷ lệ lạm phát. Trên đường này là các kết hợp giữa tỷ lệ lạm phát và tỷ lệ thất nghiệp. Dọc theo đường cong Phillips, hễ tỷ lệ thất nghiệp giảm xuống thì tỷ lệ lạm phát sẽ tăng lên; và ngược lại.

Từ đó, trường phái kinh tế học vĩ mô tổng hợp lý luận rằng để giảm tỷ lệ thất nghiệp chính phủ đã sử dụng chính sách quản lý tổng cầu, song do tỷ lệ thất nghiệp có quan hệ ngược chiều bền vững với tỷ lệ lạm phát, nên tăng trưởng kinh tế cao đương nhiên gây ra lạm phát. Lạm phát là cái giá phải trả để giảm tỷ lệ thất nghiệp.

Lý luận của chủ nghĩa tiền tệ

[sửa | sửa mã nguồn]

Chủ nghĩa tiền tệ đã bác bỏ lý luận nói trên của trường phái kinh tế học vĩ mô tổng hợp. Họ cho rằng đường cong Phillips như trên chỉ là đường cong Phillips ngắn hạn. Friedman đã đưa ra khái niệm tỷ lệ thất nghiệp tự nhiên, theo đó khi thị trường lao động ở trạng thái cân bằng vẫn có thất nghiệp. Đây là dạng thất nghiệp tự nguyện. Vì thế, ở trạng thái cân bằng, tỷ lệ thất nghiệp vẫn là một số dương. Và khi nền kinh tế cân bằng, thì lạm phát không xảy ra. Đường cong Phillips ngắn hạn dốc xuống phía phải và cắt trục hoành ở giá trị của tỷ lệ thất nghiệp tự nhiên. Hễ chính phủ áp dụng các biện pháp nhằm đưa tỷ lệ thất nghiệp xuống dưới mức này, thì giá cả sẽ tăng lên (lạm phát), và có sự dịch chuyển lên phía trái dọc theo đường cong Phillips ngắn hạn.

Sau khi lạm phát tăng tốc, cá nhân với hành vi kinh tế điển hình (hành vi duy lý) sẽ dự tính lạm phát tiếp tục tăng tốc. Trong khi tiền công danh nghĩa không đổi, lạm phát tăng nghĩa là tiền công thực tế trả cho họ giảm đi. Họ sẽ giảm cung cấp lao động, thậm chí tự nguyện thất nghiệp. Tỷ lệ thất nghiệp lại tăng lên đến mức tỷ lệ thất nghiệp tự nhiên, trong khi tỷ lệ lạm phát vẫn giữ ở mức cao.

Nếu nhà nước vẫn cố gắng giảm tỷ lệ thất nghiệp xuống dưới mức tự nhiên, cơ chế như trên lại xảy ra. Hậu quả là, trong dài hạn, tỷ lệ thất nghiệp vẫn ở mức tự nhiên mà tỷ lệ lạm phát lại bị nâng lên liên tục. Chính sách của nhà nước như vậy là chỉ có tác dụng trong ngắn hạn, còn về dài hạn là thất bại.

Tập hợp các điểm tương ứng với tỷ lệ thất nghiệp tự nhiên và các mức tỷ lệ lạm phát liên tục bị đẩy lên cao tạo thành một đường thẳng đứng. Đường này được gọi là đường Phillips dài hạn.

Chú thích và Tham khảo

[sửa | sửa mã nguồn]

^ Xem Phillips Alban W. (1958), "The relationship between unemployment and the rate of change of money wages in the UK 1861-1957," Economica.

Xem thêm

[sửa | sửa mã nguồn]

• Lạm phát
• Chủ nghĩa tiền tệ
• Lỗ hổng sản lượng

Tham khảo

[sửa | sửa mã nguồn]

1. ^ a b Phillips, A. W. (1958). “The Relationship between Unemployment and the Rate of Change of Money Wages in the United Kingdom 1861-1957”. Economica. 25 (100): 283–299. doi:10.1111/j.1468-0335.1958.tb00003.x.
2. ^ A. W. Phillips, 1958. 25 The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom 1861–1957. Economica 25(100): 283-299.
3. ^ a b c Samuelson, Paul A.; Solow, Robert M. (1960). “Analytical Aspects of Anti-Inflation Policy”. American Economic Review. 50 (2): 177–194. JSTOR 1815021.
4. ^ a b Friedman, Milton (1968). “The Role of Monetary Policy”. American Economic Review. 58 (1): 1–17. JSTOR 1831652.
5. ^ a b Phelps, Edmund S. (1968). “Money-Wage Dynamics and Labor Market Equilibrium”. Journal of Political Economy. 76 (S4): 678–711. doi:10.1086/259438. S2CID 154427979.
6. ^ a b Phelps, Edmund S. (1967). “Phillips Curves, Expectations of Inflation and Optimal Unemployment over Time”. Economica. 34 (135): 254–281. doi:10.2307/2552025. JSTOR 2552025.
7. ^ a b c Chang R., 1997. Is Low Unemployment Inflationary? Lưu trữ 2016-10-05 tại Wayback Machine Federal Reserve Bank of Atlanta Economic Review 1Q97:4-13
8. ^ a b Phelan, John (23 tháng 10 năm 2012). “Milton Friedman and the rise and fall of the Phillips Curve”. thecommentator.com. Bản gốc lưu trữ ngày 31 tháng 5 năm 2021. Truy cập ngày 29 tháng 9 năm 2014.
9. ^ “The Phillips curve may be broken for good”. The Economist. 2017.
10. ^ Hazell, Jonathon; Herreño, Juan; Nakamura, Emi; Steinsson, Jón (2022). “The Slope of the Phillips Curve: Evidence from U.S. States”. Quarterly Journal of Economics. 137 (3): 1299–1344. doi:10.1093/qje/qjac010.
11. ^ “Speech by Chair Yellen on inflation, uncertainty, and monetary policy”. Board of Governors of the Federal Reserve System (bằng tiếng Anh). Truy cập ngày 30 tháng 9 năm 2017.
12. ^ Fisher, Irving (1973). “I discovered the Phillips curve: 'A statistical relation between unemployment and price changes'”. Journal of Political Economy. 81 (2): 496–502. doi:10.1086/260048. JSTOR 1830534. S2CID 154013344. Tái bản từ ấn bản năm 1926 của International Labour Review.
13. ^ Forder, James (2014). Macroeconomics and the Phillips Curve Myth. Oxford University Press. ISBN 978-0-19-968365-9.
14. ^ Domitrovic, Brain (10 tháng 10 năm 2011). “The Economics Nobel Goes to Sargent & Sims: Attackers of the Phillips Curve”. Forbes.com. Truy cập ngày 12 tháng 10 năm 2011.
15. ^ Akerlof, George A.; Dickens, William T.; Perry, George L. (2000). “Near-Rational Wage and Price Setting and the Long-Run Phillips Curve”. Brookings Papers on Economic Activity. 2000 (1): 1–60. CiteSeerX 10.1.1.457.3874. doi:10.1353/eca.2000.0001. S2CID 14610294.
16. ^ Oliver Hossfeld, 2010. US Money Demand, Monetary Overhang, and Inflation Prediction Lưu trữ 2013-11-13 tại Wayback Machine International Network for Economic Research working paper no. 2010.4
17. ^ Jacob, Reed (2016). “AP Macroeconomics Review: Phillips Curve”. APEconReview.com.
18. ^ Blanchard, Olivier (2000). Macroeconomics (ấn bản thứ 2). Prentice Hall. tr. 149–155. ISBN 978-0-13-013306-9.
19. ^ Keynes, John Maynard (1924). Monetary Reform. New York: Hancourt. tr. 54–55. doi:10.1086/318607.
20. ^ Clarida, Richard; Galí, Jordi; Gertler, Mark (1999). “The science of monetary policy: a New-Keynesian perspective” (PDF). Journal of Economic Literature. 37 (4): 1661–1707. doi:10.1257/jel.37.4.1661. hdl:10230/360. JSTOR 2565488.
21. ^ Blanchard, Olivier; Galí, Jordi (2007). “Real Wage Rigidities and the New Keynesian Model” (PDF). Journal of Money, Credit, and Banking. 39 (s1): 35–65. doi:10.1111/j.1538-4616.2007.00015.x. hdl:1721.1/64018.
22. ^ Roberts, John M. (1995). “New Keynesian Economics and the Phillips Curve”. Journal of Money, Credit and Banking. 27 (4): 975–984. doi:10.2307/2077783. JSTOR 2077783.
23. ^ Clarida, Richard; Galí, Jordi; Gertler, Mark (2000). “Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory”. The Quarterly Journal of Economics. 115 (1): 147–180. CiteSeerX 10.1.1.111.7984. doi:10.1162/003355300554692.
24. ^ Romer, David (2012). “Dynamic Stochastic General Equilibrium Models of Fluctuation”. Advanced Macroeconomics. New York: McGraw-Hill Irwin. tr. 312–364. ISBN 978-0-07-351137-5.
25. ^ “The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1976”. The Nobel Prize. 14 tháng 10 năm 1976. Truy cập ngày 25 tháng 3 năm 2022.
26. ^ “The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2006”. The Nobel Prize. 9 tháng 10 năm 2006. Truy cập ngày 25 tháng 3 năm 2022.
27. ^ Forder, James (2010). “The historical place of the 'Friedman-Phelps' expectations critique” (PDF). European Journal of the History of Economic Thought. 17 (3): 493–511. doi:10.1080/09672560903114875. S2CID 154920593. Bản gốc (PDF) lưu trữ ngày 26 tháng 9 năm 2020. Truy cập ngày 26 tháng 11 năm 2022.
28. ^ Galbács, Peter (2015). The Theory of New Classical Macroeconomics. A Positive Critique. Contributions to Economics. Heidelberg/New York/Dordrecht/London: Springer. doi:10.1007/978-3-319-17578-2. ISBN 978-3-319-17578-2.

Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Đường cong Phillips.