Đường Elip
Có thể bạn quan tâm
Đặc điểm hình học

Elíp và một số đặc tính. F1 và F2 là các tiêu điểm; a là bán trục lớn, b là bán trục nhỏ; c là tiêu cự; e là đô let (hay tâm sai)
Elíp có hai trục đối sứng (AB, CD trên hình vẽ) vuông góc và cắt nhau tại tâm đối xứng, cắt đường elip tại các trục lớn AB và nhỏ CD. Nửa chiều dài của các trục này được gọi lần lượt là bán trục lớn (a) và bán trục nhỏ (b). Khoảng cách từ tâm e-líp đến mỗi tiêu điểm được gọi là bán tiêu cự (c).
Trong một elíp ta luôn có:
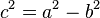
Độ dẹt của elíp (hay còn gọi là tâm sai hay độ lệch tâm của elíp) là tỉ số giữa tiêu cự và độ dài trục lớn:
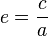 (0 ≤ e < 1)
(0 ≤ e < 1)
e = 0 khi 2 tiêu điểm trùng nhau và hình elíp lúc bấy giờ là hình tròn.
Trong hệ trục tọa độ Descartes hình elíp có thể được tạo thành bằng cách đem nhân các tọa độ x của các tất cả điểm trên một đường tròn với một hằng số đồng thời không thay đổi các tọa độ y của các điểm đó.
Diện tích của hình e-líp với các bán trục a và b được tính bởi:
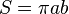
Một tính chất quang hình họccủa e-líp là: Nếu e-líp là một mặt gương cong thì một tia sáng xuất phát từ một tiêu điểm của e-líp sau khi đến mặt cong sẽ phản xạ và đi qua tiêu điểm còn lại
Hình elíp là một dạng của tiết diện hình tròn: nếu mặt của hình nón được cắt bởi một mặt phẳng không cắt mặt đáy, đường giao nhau của hình nón và mặt phẳng đó được gọi là một hình elíp. Muốn xem cách chứng minh cơ bản, đọc bài" khối dandelin".

Chú ý rằng ý nghĩa của a và b là khác so với hình bên cạnh
Biểu diễn dưới dạng phương trình đại số
Trong đại số , hình e-líp được định nghĩa bởi phương trình bậc 2 sau:

Trong đó các hệ số A, B, C, D, E, F đều là số thực 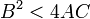 , Mỗi cặp nghiệm (x,y) tương ứng với một điểm thuộc hình elíp.
, Mỗi cặp nghiệm (x,y) tương ứng với một điểm thuộc hình elíp.


Hình E-líp
Một trường hợp đơn giản nhất, khi các bán trục của e-lip đều nằm trên các trục x và y của hệ trục tọa độ vuông góc (tọa độ Descartes) thì phương trình được đơn giản hóa thành: 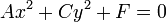
và có thể đưa về dạng chính tắc:
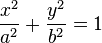
trong đó a và b là các bán trục của e-líp.
Elíp là một trong những đường cô - nic cơ bản.
Elíp tổng quát
Sự mở rộng khái niệm đường elíp lên các bậc cao khác ngoài hai hình thành đường siêu elíp

-

siêu elíp với n= 4, a= b = 1, tương tự như hình vuông được kéo các góc vào.
-

n = 3⁄2, a = b = 1 tạo ra một hình tròn hơn giống như đỉnh của hình vuông bị vát tròn.
-

n = 1⁄2, a = b = 1 có hình sao 4 cạnh dạng Parapol

Tổng quát hơn nữa, ta có trường hợp đường elíp với hai số mũ khác nhau: m≠n
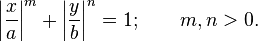
nghĩa là:
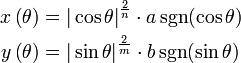
-
Mở rộng lên không gian ba chiều, ta có superellipsoid

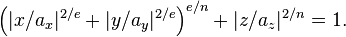
Các phương trình tham số trong mặt phẳng chứa các tham số u và v gồm :

với các phương trình bổ trợ

và hàm sgn(x) được định nghĩa như sau

Thể tích giới hạn bởi mặt này có thể được tính thông qua hàm beta, β(m,n) = Γ(m)Γ(n)/Γ(m+n):
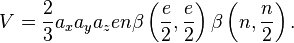
Từ khóa » Tính Chất Của đường Elip
-
Elíp – Wikipedia Tiếng Việt
-
Lý Thuyết Elip Toán 10
-
Lý Thuyết Elip Toán 10
-
Định Nghĩa , Công Thức Elip Kèm Bài Tập (có đáp án)
-
Chuyên đề Elip - Chuyên đề Toán THPT - Diễn đàn Toán Học
-
Lý Thuyết Phương Trình đường Elip | SGK Toán Lớp 10
-
Bài 3. Phương Trình đường Elip - Củng Cố Kiến Thức
-
Đường Elip Là Gì? Phương Trình Elip Là Gì? Tìm Hiểu Phương
-
Hình Elip Là Gì? Công Thức Tính Chu Vi, Diện Tích Hình Elip
-
Phương Trình Elip
-
Phương Trình Elip Và Bộ Công Thức Tính Diện Tính Hình Elip - TopLoigiai
-
Phương Trình Elip Và Bộ Công Thức Tính Diện Tính Hình Elip
-
Lý Thuyết Phương Trình đường Elip Hay, Chi Tiết - Toán Lớp 10