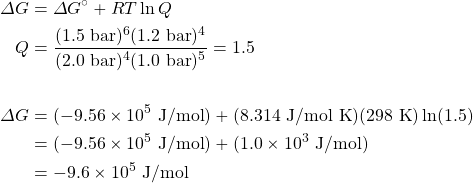Free Energy Under Nonstandard Conditions – Introductory Chemistry

Trang chủ » G=g0+rt Ln Q » Free Energy Under Nonstandard Conditions – Introductory Chemistry

Có thể bạn quan tâm

  • To be able to determine free energy at nonstandard conditions using the standard change in Gibbs free energy, ΔG°.
  • To understand and use the relationship between ΔG° and the equilibrium constant K.

Many reactions do not occur under standard conditions, and therefore we need some ways of determining the free energy under nonstandard conditions.

Using Standard Change in Gibbs Free Energy, ΔG°

The change in Gibbs free energy under nonstandard conditions, ΔG, can be determined from the standard change in Gibbs free energy, ΔG°:

\Delta G=\Delta G^{\circ}+RT \ln Q

where R is the ideal gas constant 8.314 J/mol K, Q is the reaction quotient, and T is the temperature in Kelvin.

Under standard conditions, the reactant and product solution concentrations are 1 M, or the pressure of gases is 1 bar, and Q is equal to 1. Taking the natural logarithm simplifies the equation to:

\Delta G=\Delta G^{\circ}\text{ (under standard conditions)}

Under nonstandard conditions, Q must be calculated (in a manner similar to the calculation for an equilibrium constant). For gases, the concentrations are expressed as partial pressures in the units of either atmospheres or bars, and solutes in the units of molarity.

For the reaction aA + bB\leftrightharpoons cC+dD:

Q_{\text{gases}}=\dfrac{\left(P_C\right)^c\left(P_D\right)^d}{\left(P_A\right)^a\left(P_B\right)^b}\hspace{2em}\text{or}\hspace{2em}Q_{\text{solutes}}=\dfrac{[C]^c[D]^d}{[A]^a[B]^b}

Consider the following reaction:

4NH3(g) + 5O2(g) ⇌ 6H2O(g) + 4NO(g)

  1. Use the thermodynamic data in the appendix to calculate ΔG° at 298 K.
  2. Calculate ΔG at 298 K for a mixture of 2.0 bar NH3(g), 1.0 bar O2(g), 1.5 bar H2O(g), and 1.2 bar NO(g).

Solution

  1. \phantom{start}

    \begin{align*} \Delta G^{\circ}&=\underset{\text{products}}{\sum n\Delta G^{\circ}{}_{\text{f}}}-\underset{\text{reactants}}{\sum m\Delta G^{\circ}{}_{\text{f}}} \\ &=[(6\times -228.6\text{ kJ/mol})+(4\times 87.6\text{ kJ/mol})] \\ &\phantom{=}-[(4\times -16.4\text{ kJ/mol})+(5\times 0.0\text{ kJ/mol})] \\ &=(-1021.2\text{ kJ/mol})-(-65.6\text{ kJ/mol}) \\ &=-955.6\text{ kJ/mol}=-9.56\times 10^5\text{ J/mol} \end{align*}

  2. \phantom{start}

    \begin{align*} \Delta G&=\Delta G^{\circ}+RT \ln Q \\ Q&=\dfrac{(1.5\text{ bar})^6(1.2\text{ bar})^4}{(2.0\text{ bar})^4(1.0\text{ bar})^5}=1.5 \\ \\ \Delta G&=(-9.56\times 10^5\text{ J/mol})+(8.314\text{ J/mol K})(298\text{ K})\ln(1.5) \\ &=(-9.56\times 10^5\text{ J/mol})+(1.0\times 10^3\text{ J/mol}) \\ &=-9.6\times 10^5\text{ J/mol} \end{align*}

The Relationship between ΔG° and K

There is a direct relationship between ΔG⁰ and the equilibrium constant K. We can establish this relationship by substituting the equilibrium values (ΔG = 0, and K = Q) into the equation for determining free energy change under nonstandard conditions:

\begin{align*} \Delta G&=\Delta G^{\circ}+RT\ln Q \\ 0&=\Delta G^{\circ}+RT\ln K \\ \Delta G^{\circ}&=-RT\ln K \end{align*}

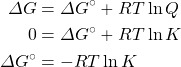
We now have a way of  relating the equilibrium constant directly to changes in enthalpy and entropy. As well, we can now determine the equilibrium constant from thermochemical data tables or determine the standard free energy change from equilibrium constants.

The Ksp for CuI(s) at 25°C is 1.27 × 10−12. Determine ΔG° for the following:

Cu+(aq) + I−(aq) → CuI(s)

Solution

\Delta G^{\circ}=-RT\ln K

The equation given is in the opposite direction to the definition of Ksp:

\begin{align*} K&=\dfrac{1}{K_{\text{sp}}}=\left(\dfrac{1}{1.27}\times 10^{-12}\right)=7.87\times 10^{11} \\ \\ \Delta G^{\circ}&=-(8.314\text{ J/mol K})(298\text{ K})\ln(7.87\times 10^{11}) \\ &=-(8.314\text{ J/mol K})(298\text{ K})(27.4) \\ &=-6.79\times 10^4\text{ J/mol}=-67.9\text{ kJ/mol} \\ \end{align*}

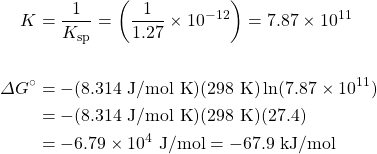
  • The free energy at nonstandard conditions can be determined using ΔG = ΔG° + RT ln Q.
  • There is a direct relationship between ΔG° and the equilibrium constant K: ΔG° = −RT ln K.

Từ khóa » G=g0+rt Ln Q