Giải Bài 6, 7, 8, 9, 10 Trang 92 Sách Giáo Khoa Hình Học 11

Bài 6 trang 92 sgk hình học 11

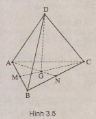
Cho hình tứ diện \(ABCD\). Gọi \(G\) là trọng tâm tam giác \(ABC\). Chứng minh rằng: \(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=3\overrightarrow{DG}.\)

Giải

(H.3.5)

 \(VT=\overrightarrow{DG}+\overrightarrow{GA}+\overrightarrow{DG}+\overrightarrow{GB}+\overrightarrow{DG}+\overrightarrow{GC}\)

         \(=3\overrightarrow{DG}=VP\) (đpcm)

 

Bài 7 trang 92 sgk hình học 11

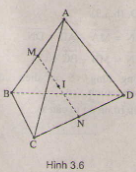
Gọi \(M\) và \(N\) lần lượt là trung điểm của các cạnh \(AC\) và \(BD\) của tứ diện \(ABCD\). Gọi \(I\) là trung điểm của đoạn thẳng \(MN\) và \(P\) là một điểm bất kì trong không gian. Chứng minh rằng: 

a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0};\)

b) \(\overrightarrow{PI}=\frac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}).\)

Giải

(H.3.6)

a) \(\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IM},\)

    \(\overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{IN}.\)

Cộng từng vế ta được :

\(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}.\)

b) \(\overrightarrow{PI}=\overrightarrow{PA}+\overrightarrow{AI},\)

    \(\overrightarrow{PI}=\overrightarrow{PB}+\overrightarrow{BI},\)

    \(\overrightarrow{PI}=\overrightarrow{PC}+\overrightarrow{CI},\)

    \(\overrightarrow{PI}=\overrightarrow{PD}+\overrightarrow{DI}.\)

Cộng từng vế ta được:

\(4\overrightarrow {PI}  = \overrightarrow {PA}  + \overrightarrow {PB}  + \overrightarrow {PC}  + \overrightarrow {PD}  + (\overrightarrow {AI}  + \overrightarrow {BI} ) + (\overrightarrow {CI}  + \overrightarrow {DI} )\)

\( \Leftrightarrow\)\({PI}=\frac{1}{4} (\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}).\)

 

Bài 8 trang 92 sgk hình học 11

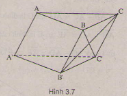
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có  \(\overrightarrow{AA'}\) = \(\overrightarrow{a}\), \(\overrightarrow{AB}\) = \(\overrightarrow{b}\), \(\overrightarrow{AC}\) = \(\overrightarrow{c}\). Hãy phân tích (hay biểu thị véctơ \(\overrightarrow{B'C}\), \(\overrightarrow{BC'}\) qua các véctơ \(\overrightarrow{a}\),\(\overrightarrow{b}\), \(\overrightarrow{c}\).

Giải

(H.3.7)

\(\overrightarrow{B'C}\) = \(\overrightarrow{B'A'}\) + \(\overrightarrow{A'A}\) + \(\overrightarrow{AC}\) = - \(\overrightarrow{b}\) - \(\overrightarrow{a}\) + \(\overrightarrow{c}\).

 \(\overrightarrow{BC'}\) = \(\overrightarrow{BA}\) + \(\overrightarrow{AA'}\) + \(\overrightarrow{A'C'}\) = - \(\overrightarrow{b}\) + \(\overrightarrow{a}\) + \(\overrightarrow{c}\).

Nhận xét: ba véctơ \(\overrightarrow{a}\); \(\overrightarrow{b}\); \(\overrightarrow{c}\) ở trên gọi là bộ ba véctơ cơ sở )dùng để phân tích các véctơ khác).

 

Bài 9 trang 92 sgk hình học 11

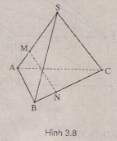
Cho tam giác \(ABC\). Lấy điểm \(S\) nằm ngoài mặt phẳng \((ABC)\). Trên đoạn \(SA\) lấy điểm \(M\) sao cho \(\overrightarrow{MS}\) = \(-2\overrightarrow{MA}\) và trên đoạn \(BC\) lấy điểm \(N\) sao cho \(\overrightarrow{NB}=-\frac{1}{2}\overrightarrow{NC}.\) Chứng minh rằng ba véctơ  \(\overrightarrow{AB}\), \(\overrightarrow{MN}\), \(\overrightarrow{SC}\) đồng phẳng.

Giải

(H.3.8)

\(\overrightarrow{MN}\) = \(\overrightarrow{MS}\) + \(\overrightarrow{SC}\) + \(\overrightarrow{CN}\)

          = \(\frac{2}{3}\overrightarrow{AS}\) + \(\overrightarrow{SC}\) + \(\frac{2}{3}\overrightarrow{CB}.\) (1)

\(\overrightarrow{MN}\) = \(\overrightarrow{MA}\) + \(\overrightarrow{AB}\) + \(\overrightarrow{BN}\)

          = \(-\frac{1}{3}\overrightarrow{AS}\) + \(\overrightarrow{AB}\) + \(-\frac{1}{3}\overrightarrow{CB}.\) (2)

Nhân (2) với 2 rồi cộng với (1) ta được:

\(3\overrightarrow{MN}\) = \(\overrightarrow{SC}\) + \(2\overrightarrow{AB}\) \(\Leftrightarrow\overrightarrow{MN}= \frac{1}{3}\overrightarrow{SC}+\frac{2}{3}\overrightarrow{AB}.\)

Vậy \(\overrightarrow{AB}\), \(\overrightarrow{MN}\), \(\overrightarrow{SC}\) đồng phẳng.

 

Bài 10 trang 92 sgk hình học 11

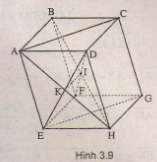
Cho hình hộp \(ABCD.EFGH\). Gọi \(K\) là giao điểm của \(AH\) và \(DE\), \(I\) là giao điểm của \(BH\) và \(DF\). Chứng minh ba véctơ \(\overrightarrow{AC}\), \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) đồng phẳng.

Giải

(H.3.9) Chứng minh giá của các véctơ \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) song song với mặt phẳng \((ABCD)\) chứa véctơ \(\overrightarrow{AC}\). Từ đó suy ra ba véctơ đồng phẳng.

\(I=BH\cap DF\) là giao điểm của hai đường chéo hình bình hành \(BDHF\) do đó \(I\) là trung điểm của \(BH\)  (1)

\(K\) là giao điểm của hai đường chéo hình bình hành \(ADHE\) do đó \(K\) là trung điểm của \(AH\)                  (2)

Từ (1) và (2) suy ra \(KI\) là đường trung bình của tam giác \(ABH\). Do đó \(KI//AB\) suy ra \(KI//(ABCD)\)      (*)

Ta có: \(BCGF\) là hình bình hành nên \(FG//BC\) suy ra \(FG//(ABCD)\)                                                         (2*)

Từ (*) và (2*) suy ra: \(\overrightarrow{AC}\), \(\overrightarrow{KI}\), \(\overrightarrow{FG}\) đồng phẳng.

Giaibaitap.me