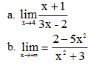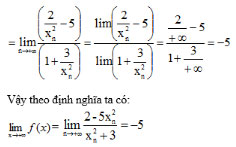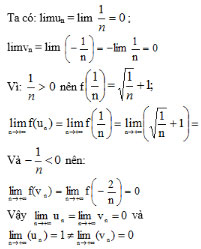Giải Bài Tập Toán 11 Bài 2: Giới Hạn Của Hàm Số
Có thể bạn quan tâm
-
-

-
Mầm non
-
Lớp 1
-
Lớp 2
-
Lớp 3
-
Lớp 4
-
Lớp 5
-
Lớp 6
-
Lớp 7
-
Lớp 8
-
Lớp 9
-
Lớp 10
-
Lớp 11
-
Lớp 12
-
Thi vào lớp 6
-
Thi vào lớp 10
-
Thi Tốt Nghiệp THPT
-
Đánh Giá Năng Lực
-
Khóa Học Trực Tuyến
-
Hỏi bài
-
Trắc nghiệm Online
-
Tiếng Anh
-
Thư viện Học liệu
-
Bài tập Cuối tuần
-
Bài tập Hàng ngày
-
Thư viện Đề thi
-
Giáo án - Bài giảng
-
Tất cả danh mục
-
- Mầm non
- Lớp 1
- Lớp 2
- Lớp 3
- Lớp 4
- Lớp 5
- Lớp 6
- Lớp 7
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
- Lớp 12
- Thi Chuyển Cấp
-
- Hôm nay +3
- Ngày 2 +3
- Ngày 3 +3
- Ngày 4 +3
- Ngày 5 +3
- Ngày 6 +3
- Ngày 7 +5
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ ZaloGiải bài tập Toán 11 Giải tích: Giới hạn của hàm số
VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 11 bài 2: Giới hạn của hàm số, nội dung tài liệu gồm 7 bài tập trang 132, 133 SGK kèm theo lời giải chi tiết sẽ giúp các bạn học sinh học tập hiệu quả hơn môn Toán. Mời thầy cô cùng các bạn học sinh tham khảo.
Giải bài tập Toán 11 bài 2: Dãy số
Giải bài tập Toán 11 bài 3: Cấp số cộng
Giải bài tập Toán 11 bài 4: Cấp số nhân
Giải bài tập Toán 11 ôn tập chương 3: Dãy số - Cấp số cộng và cấp số nhân
Giải bài tập Toán 11 Giới hạn của hàm số
Bài 1 (trang 132 SGK Đại số 11): Dùng định nghĩa tìm các giới hạn sau:
Lời giải:

Bài 2 (trang 132 SGK Đại số 11):
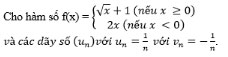
Tính limun, limvn, limf(un), limf(vn).
Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0?
Lời giải:
Bài 3 (trang 132 SGK Đại số 11): Tính các giới hạn sau:
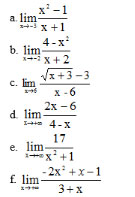
Lời giải:
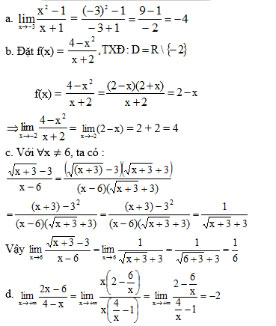
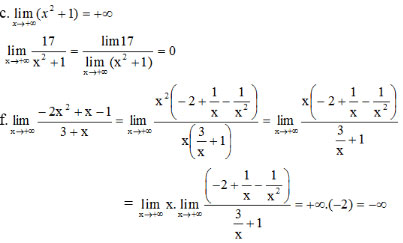
Bài 4 (trang 132 SGK Đại số 11): Tìm các giới hạn sau:
![]() \(a) \underset{x\rightarrow 2}{lim}\frac{3x -5}{(x-2)^{2}};\)
\(a) \underset{x\rightarrow 2}{lim}\frac{3x -5}{(x-2)^{2}};\)
![]() \(b) \underset{x\rightarrow 1^{-}}{lim}\frac{2x -7}{x-1};\)
\(b) \underset{x\rightarrow 1^{-}}{lim}\frac{2x -7}{x-1};\)
![]() \(c) \underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}.\)
\(c) \underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}.\)
Lời giải:
a) Ta có
![]() \(\underset{x\rightarrow 2}{\lim} (x - 2)^2= 0 và (x - 2)^2> 0 với ∀x ≠ 2 và \underset{x\rightarrow 2}{\lim} (3x - 5) = 3.2 - 5 = 1 > 0\)
\(\underset{x\rightarrow 2}{\lim} (x - 2)^2= 0 và (x - 2)^2> 0 với ∀x ≠ 2 và \underset{x\rightarrow 2}{\lim} (3x - 5) = 3.2 - 5 = 1 > 0\)
Do đó ![]() \(\underset{x\rightarrow 2}{\lim}\frac{3x -5}{(x-2)^{2}} = +∞\).
\(\underset{x\rightarrow 2}{\lim}\frac{3x -5}{(x-2)^{2}} = +∞\).
b) Ta có
![]() \(\underset{x\rightarrow 1^{-}}{\lim} (x - 1)=0 và x - 1 < 0 với ∀x < 1 và \underset{x\rightarrow 1^{-}}{\lim} (2x - 7) = 2.1 - 7 = -5 <0.\)
\(\underset{x\rightarrow 1^{-}}{\lim} (x - 1)=0 và x - 1 < 0 với ∀x < 1 và \underset{x\rightarrow 1^{-}}{\lim} (2x - 7) = 2.1 - 7 = -5 <0.\)
Do đó ![]() \(\underset{x\rightarrow 1^{-}}{\lim}\frac{2x -7}{x-1} = +∞\).
\(\underset{x\rightarrow 1^{-}}{\lim}\frac{2x -7}{x-1} = +∞\).
c) Ta có
![]() \(\underset{x\rightarrow 1^{+}}{\lim} (x - 1) = 0 và x - 1 > 0 với ∀x > 1 và \underset{x\rightarrow 1^{+}}{\lim} (2x - 7) = 2.1 - 7 = -5 < 0\)
\(\underset{x\rightarrow 1^{+}}{\lim} (x - 1) = 0 và x - 1 > 0 với ∀x > 1 và \underset{x\rightarrow 1^{+}}{\lim} (2x - 7) = 2.1 - 7 = -5 < 0\)
Do đó ![]() \(\underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}= -∞.\)
\(\underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}= -∞.\)
Bài 5 (trang 133 SGK Đại số 11): Cho hàm số f(x) = ...
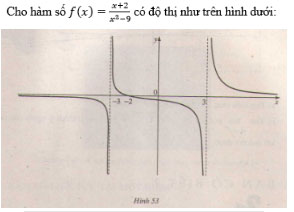
a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
![]() \(x →- ∞, x →3^-, x →-3^+\)
\(x →- ∞, x →3^-, x →-3^+\)
b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
![]() \(\underset{x\rightarrow -\infty }{\lim} f(x) với f(x)\) được xét trên khoảng
\(\underset{x\rightarrow -\infty }{\lim} f(x) với f(x)\) được xét trên khoảng ![]() \((-\infty; -3),\)
\((-\infty; -3),\)
![]() \(\underset{x\rightarrow 3^{-}}{\lim} f(x) với f(x)\)được xét trên khoảng
\(\underset{x\rightarrow 3^{-}}{\lim} f(x) với f(x)\)được xét trên khoảng ![]() \((-3,3),\)
\((-3,3),\)
![]() \(\underset{x\rightarrow -3^{+}}{lim} f(x) với f(x)\) được xét trên khoảng
\(\underset{x\rightarrow -3^{+}}{lim} f(x) với f(x)\) được xét trên khoảng ![]() \((-3; 3).\)
\((-3; 3).\)
Lời giải:
a) Quan sát đồ thị ta thấy ![]() \(x → -∞ thì f(x) → 0; khi x → 3^- thì f(x) → -∞;\)
\(x → -∞ thì f(x) → 0; khi x → 3^- thì f(x) → -∞;\)
![]() \(khi x → -3^+ thì f(x) → +∞.\)
\(khi x → -3^+ thì f(x) → +∞.\)
 \(b) \underset{x\rightarrow -\infty }{lim} f(x) = \underset{x\rightarrow -\infty }{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -\infty }{lim}\frac{\frac{1}{x}+\frac{2}{x^{2}}}{1-\frac{9}{x^{2}}} = 0.\)
\(b) \underset{x\rightarrow -\infty }{lim} f(x) = \underset{x\rightarrow -\infty }{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -\infty }{lim}\frac{\frac{1}{x}+\frac{2}{x^{2}}}{1-\frac{9}{x^{2}}} = 0.\)
![]() \(\underset{x\rightarrow 3^{-}}{lim} f(x) = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3}.\frac{1}{x-3} = -∞ vì \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3} = \frac{5}{6} > 0 và \underset{x\rightarrow 3^{-}}{\lim} \frac{1}{x-3} = -∞.\)
\(\underset{x\rightarrow 3^{-}}{lim} f(x) = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3}.\frac{1}{x-3} = -∞ vì \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3} = \frac{5}{6} > 0 và \underset{x\rightarrow 3^{-}}{\lim} \frac{1}{x-3} = -∞.\)
![]() \(\underset{x\rightarrow -3^{+}}{lim} f(x) =\underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} . \frac{1}{x+3} = +∞ vì \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} = \frac{-1}{-6} = \frac{1}{6} > 0 và \underset{x\rightarrow -3^{+}}{lim}\frac{1}{x+3} = +∞.\)
\(\underset{x\rightarrow -3^{+}}{lim} f(x) =\underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} . \frac{1}{x+3} = +∞ vì \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} = \frac{-1}{-6} = \frac{1}{6} > 0 và \underset{x\rightarrow -3^{+}}{lim}\frac{1}{x+3} = +∞.\)
Bài 6 (trang 133 SGK Đại số 11): Tính:
Tính:
 \(\eqalign{ & a)\mathop {\lim }\limits_{x \to + \infty } ({x^4} - {x^2} + x - 1) \cr & b)\mathop {\lim }\limits_{x \to - \infty } ( - 2{x^3} + 3{x^2} - 5) \cr & c)\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr & d)\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr}\)
\(\eqalign{ & a)\mathop {\lim }\limits_{x \to + \infty } ({x^4} - {x^2} + x - 1) \cr & b)\mathop {\lim }\limits_{x \to - \infty } ( - 2{x^3} + 3{x^2} - 5) \cr & c)\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr & d)\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr}\)
Lời giải:
 \(\begin{array}{l} a)\,\,\mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) \\= \mathop {\lim }\limits_{x \to + \infty } {x^4}\left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right)\\ \mathop {\lim }\limits_{x \to + \infty } {x^4} = + \infty \\ \mathop {\lim }\limits_{x \to + \infty } \left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) = + \infty \\\end{array}\)
\(\begin{array}{l} a)\,\,\mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) \\= \mathop {\lim }\limits_{x \to + \infty } {x^4}\left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right)\\ \mathop {\lim }\limits_{x \to + \infty } {x^4} = + \infty \\ \mathop {\lim }\limits_{x \to + \infty } \left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) = + \infty \\\end{array}\)
 \(\begin{array}{l} b)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 3{x^2} - 5} \right) \\= \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right)\\ \mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = - 2 < 0\\ \Leftrightarrow \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = + \infty \\\end{array}\)
\(\begin{array}{l} b)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 3{x^2} - 5} \right) \\= \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right)\\ \mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = - 2 < 0\\ \Leftrightarrow \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = + \infty \\\end{array}\)
![\begin{array}{l} c)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - x\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right]\\ \mathop {\lim }\limits_{x \to - \infty } \left( { - x} \right) = + \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = + \infty \\\end{array}](https://st.vndoc.com/data/image/blank.png) \(\begin{array}{l} c)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - x\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right]\\ \mathop {\lim }\limits_{x \to - \infty } \left( { - x} \right) = + \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = + \infty \\\end{array}\)
\(\begin{array}{l} c)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - x\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right]\\ \mathop {\lim }\limits_{x \to - \infty } \left( { - x} \right) = + \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = + \infty \\\end{array}\)
 \(\begin{array}{l} d)\,\,\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} + x}}{{5 - 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\sqrt {1 + \frac{1}{{{x^2}}}} + 1} \right)}}{{5 - 2x}}\\ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} + 1}}{{\frac{5}{x} - 2}} = \frac{{1 + 1}}{{ - 2}} = - 1 \end{array}\)
\(\begin{array}{l} d)\,\,\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} + x}}{{5 - 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\sqrt {1 + \frac{1}{{{x^2}}}} + 1} \right)}}{{5 - 2x}}\\ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} + 1}}{{\frac{5}{x} - 2}} = \frac{{1 + 1}}{{ - 2}} = - 1 \end{array}\)
Bài 7 (trang 133 SGK Đại số 11): Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và ảnh A'B' của nó tới quang tâm O của thấu kính (hình dưới).
Lời giải:
a) Từ hệ thức
Từ khóa » Giải Bài Tập Giới Hạn Của Hàm Số Lớp 11
-
Giải Toán 11 Bài 2: Giới Hạn Của Hàm Số
-
Giới Hạn Của Hàm Số - Toán 11
-
Giải Toán Lớp 11 Bài 1, 2, 3, 4, 5, 6, 7 Trang 132, 133 SGK Đại Số
-
50 Bài Tập Về Giới Hạn Của Hàm Số (có đáp án 2022) – Toán 11
-
Giới Hạn Của Hàm Số Lớp 11: Lý Thuyết, Công Thức, Bài Tập Từ A - Z
-
Toán 11 - Giới Hạn Của Hàm Số, Cách Tính Và Bài Tập áp Dụng
-
Sách Giải Bài Tập Toán Lớp 11 Bài 2: Giới Hạn Của Hàm Số
-
Giải Bài Tập SGK Toán 11 Bài 2: Giới Hạn Của Hàm Số
-
Bài Tập Giới Hạn Hàm Số - Môn Toán 11 – Thầy Nguyễn Công Chính
-
Toán 11 Bài 2: Giới Hạn Của Hàm Số - Hoc247
-
Giải Bài Tập Toán 11 Bài 2. Giới Hạn Của Hàm Số
-
Giới Hạn Hàm Số Lớp 11: Lý Thuyết, Công Thức, Bài Tập - Boxthuthuat
-
Giới Hạn Của Hàm Số - Giải Bài Tập SGK Toán 11
-
Hướng Dẫn Giải Bài Tập Giới Hạn Hàm Số Lớp 11 - Hocmai