Giải Bài Tập Toán 12 Bài 1: Lũy Thừa (Hay Nhất)

Nội dung bài viết

1. Giải Toán 12 Bài 1: Lũy Thừa
   1. Trả lời câu hỏi bài 1: Luỹ thừa 12
      1. Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 49: 
      2. Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 50: 
      3. Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 52: 
      4. Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 54: 
      5. Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 55:
      6. Rút gọn biểu thức:
   2. Giải bài tập SGK Toán 12 bài Lũy thừa
      1. Bài 1 (trang 55 SGK Giải tích 12): 
      2. Bài 2 (trang 55 SGK Giải tích 12): 

Nội dung hướng dẫn giải bài tập SGK Toán 12 chương 2 bài 1 lũy thừa sẽ giúp các em học sinh củng cố lại kiến thức về lũy thừa thông qua việc ứng dụng phương pháp và công thức giải bài toán lũy thừa nhanh, ngắn gọn từ đội ngũ chuyên gia của chúng tôi.

Tham khảo bài học trước đó:

• Khảo sát sự biến thiên và vẽ đồ thị hàm số - Giải Toán 12
• Giải bài tập Toán 12 Đường tiệm cận (Hay nhất)
• Giải Toán 12: Giá trị lớn nhất nhỏ nhất của hàm số (Hay nhất)

Giải Toán 12 Bài 1: Lũy Thừa

Trả lời câu hỏi bài 1: Luỹ thừa 12

Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 49: 

Tính (1,5)4; ((-2)/3)3; (√3)5.

Lời giải:

(1,5)4 = 5.0625; ((-2)/3)3=(-8)/27; (√3)5 = 9√3

Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 50: 

Dựa vào đồ thị của các hàm số y = x3 và y = x4 (H.26, H.27), hãy biện luận theo b số nghiệm của các phương trình x3 = b và x4 = b.

Lời giải:

Số nghiệm của phương trình x3 = b là số giao điểm của hai đồ thị hàm số y = b và y = x3.

Dựa vào H26 ta có đồ thị hàm số y = x3 luôn cắt đường thẳng y = b tại một điểm duy nhất với mọi b nên phương trình x3 = b luôn có nghiệm duy nhất với mọi b.

Số nghiệm của phương trình x4 = b (1) là số giao điểm của hai đồ thị hàm số y = b và y = x4. Dựa và hình 27 ta có:

+ Với b < 0 hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.

+ Với b = 0, hai đồ thị hàm số tiếp xúc nhau tại (0,0), vậy phương trình (1) có nghiệm duy nhất x = 0.

+ Với b > 0, hai đồ thị hàm số cắt nhau tại hai điểm phân biết, vậy phương trình (1) có hai nghiệm phân biệt.

Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 52: 

Chứng minh tính chất n√a . n√b = n√ab.

Lời giải:

Đặt n√a = x, n√b = y. Khi đó: xn = a, yn = b.

Ta có (xy)n = xn.yn = a.b. Vậy xy là căn bậc n của ab.

Suy ra n√ab = xy = n√a.n√b

Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 54: 

Hãy nhắc lại các tính chất của lũy thừa với số mũ nguyên dương.

Lời giải:

Các tính chất về đẳng thức

1. am. an = a(m+n)

2. am : an = a(m-n) (m ≥ n).

3. (am)n = amn

4.(a/b)m = am / bm (b ≠ 0)

5. (ab)m = am.bm

Các tính chất về bất đẳng thức

Với a > 1 thì am > an ⇔ m > n.

Với 0 < a < 1 thì am > an ⇔ m < n.

0 < a < b thì am > bm

Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 55:

Rút gọn biểu thức:

Lời giải:

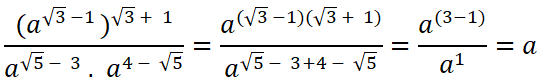
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 55:

So sánh các số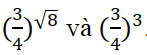 

Lời giải:

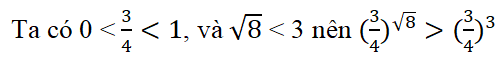
Giải bài tập SGK Toán 12 bài Lũy thừa

Bài 1 (trang 55 SGK Giải tích 12): 

Tính

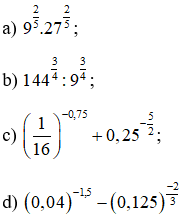
Lời giải:

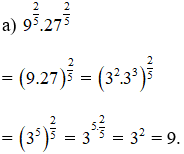
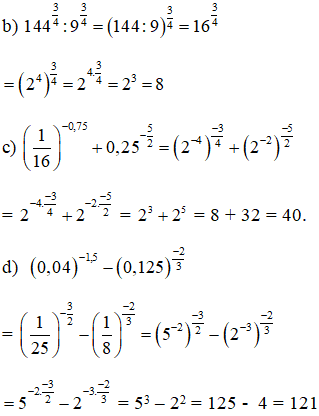
Bài 2 (trang 55 SGK Giải tích 12): 

Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:

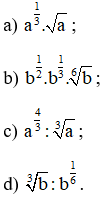
Lời giải:

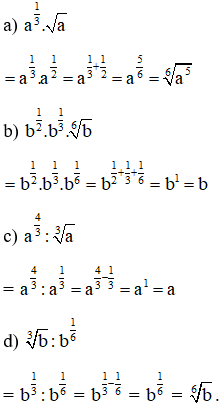
Nội dung giải bài tập Toán 12 bài 1 lũy thừa còn tiếp, mời các em xem full tại file tải về miễn phí...

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về lời giải bài tập SGK Bài 1: Lũy thừa file Word, pdf hoàn toàn miễn phí!