Giải Bài Tập Toán 12 Nâng Cao Chương 1 Bài 3: GTLN-GTNN Của ...

Trang chủ » Gtln Gtnn Của Hàm Số 12 » Giải Bài Tập Toán 12 Nâng Cao Chương 1 Bài 3: GTLN-GTNN Của ...

Có thể bạn quan tâm

Giải bài tập Toán 12 Nâng cao Chương 1 bài 3: GTLN-GTNN của hàm số Giải SGK Toán 12 Nâng cao trang 22, 23, 24 Bài trước Tải về Bài sau Lớp: Lớp 12 Môn: Toán Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Giải bài tập sgk Toán 12 Nâng cao bài 3 Đại số và Giải tích giúp các em giải các bài tập trong sách giáo khoa Toán 12 nâng cao. Tài liệu hướng dẫn các em làm quen với các dạng bài tập về GTLN, GTNN của hàm số.

Giải bài tập SGK Toán 12 Nâng cao bài 3

  • Bài 16 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 17 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 18 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 19 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 20 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 21 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 22 trang 23 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 23 trang 23 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 24 trang 23 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 25 trang 23 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 26 trang 23 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 27 trang 24 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3
  • Bài 28 trang 24 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3

Bài 16 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: f\left( x \right) = {\sin ^4}x + {\cos ^4}x\(f\left( x \right) = {\sin ^4}x + {\cos ^4}x\)

Giải

TXĐ: D=\mathbb R\(D=\mathbb R\)

\eqalign{ & f\left( x \right) = {\left( {{{\sin }^2}x} \right)^2} + {\left( {{{\cos }^2}x} \right)^2} + 2{\sin ^2}x{\cos ^2}x - 2{\sin ^2}x{\cos ^2}x \cr & \,\,\,\,\,\,\,\,\,\,\, = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x = 1 - {1 \over 2}{\sin ^2}2x \cr}\(\eqalign{ & f\left( x \right) = {\left( {{{\sin }^2}x} \right)^2} + {\left( {{{\cos }^2}x} \right)^2} + 2{\sin ^2}x{\cos ^2}x - 2{\sin ^2}x{\cos ^2}x \cr & \,\,\,\,\,\,\,\,\,\,\, = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x = 1 - {1 \over 2}{\sin ^2}2x \cr}\)

Vì 0 \le {\sin ^2}2x \le 1 nên: \,\,f\left( x \right) \le 1 với mọi x \in {\mathbb{R}},f\left( 0 \right) = 1. Vậy \mathop {\max f\left( x \right)}\limits_{x \in {\mathbb {R}}} = 1\(0 \le {\sin ^2}2x \le 1 nên: \,\,f\left( x \right) \le 1 với mọi x \in {\mathbb{R}},f\left( 0 \right) = 1. Vậy \mathop {\max f\left( x \right)}\limits_{x \in {\mathbb {R}}} = 1\)

*\,\,\,f\left( x \right) \ge {1 \over 2} với mọi x \in {\mathbb{R}},f\left( {{\pi \over 4}} \right) = 1 - {1 \over 2} = {1 \over 2}\(*\,\,\,f\left( x \right) \ge {1 \over 2} với mọi x \in {\mathbb{R}},f\left( {{\pi \over 4}} \right) = 1 - {1 \over 2} = {1 \over 2}\)

Vậy \mathop {\min f\left( x \right)}\limits_{x \in {\mathbb {R}}} = {1 \over 2}\(\mathop {\min f\left( x \right)}\limits_{x \in {\mathbb {R}}} = {1 \over 2}\)

Bài 17 trang 22 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a)f\left( x \right) = {x^2} + 2x - 5 trên đoạn \left[ { - 2;3} \right]\(f\left( x \right) = {x^2} + 2x - 5 trên đoạn \left[ { - 2;3} \right]\)

b) f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4\(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4\) trên đoạn \left[ { - 4;0} \right]\(\left[ { - 4;0} \right]\)

c)f\left( x \right) = x + {1 \over x}\(f\left( x \right) = x + {1 \over x}\)trên đoạn \left( {0; + \infty } \right)\(\left( {0; + \infty } \right)\)

d) f\left( x \right) = - {x^2} + 2x + 4\(f\left( x \right) = - {x^2} + 2x + 4\) trên đoạn \left[ {2;4} \right]\(\left[ {2;4} \right]\)

e) f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn\left[ {0;1} \right]\(\left[ {0;1} \right]\)

f) f\left( x \right) = x - {1 \over x}\(f\left( x \right) = x - {1 \over x}\)trên đoạn \left( {0;2} \right]\(\left( {0;2} \right]\)

Giải

a)D = \left[ { - 2;3} \right];f\(D = \left[ { - 2;3} \right];f'\left( x \right) = 2x + 2;f'\left( x \right) = 0 \Leftrightarrow x=- 1 \in \left[ { - 2;3} \right]\)

Ta có: f\left( { - 2} \right) = - 5;f\left( { - 1} \right) = - 6;f\left( 3 \right) = 10\(f\left( { - 2} \right) = - 5;f\left( { - 1} \right) = - 6;f\left( 3 \right) = 10\)

Vậy: \mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 2;3} \right]} = - 6;\,\,\,\,\,\,\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { - 2;3} \right]}\(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 2;3} \right]} = - 6;\,\,\,\,\,\,\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { - 2;3} \right]}\)

b)

D = \left[ { - 4;0} \right];\,f\(D = \left[ { - 4;0} \right];\,f'\left( x \right) = {x^2} + 4x + 3;f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \in \left[ { - 4;0} \right] \hfill \cr x = - 3 \in \left[ { - 4;0} \right] \hfill \cr} \right.\)

Ta có: f\left( { - 4} \right) = - {{16} \over 3};f\left( { - 1} \right) = - {{16} \over 3};f\left( { - 3} \right) = - 4;f\left( 0 \right) = - 4\(f\left( { - 4} \right) = - {{16} \over 3};f\left( { - 1} \right) = - {{16} \over 3};f\left( { - 3} \right) = - 4;f\left( 0 \right) = - 4\)

Vậy\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - {{16} \over 3};\,\,\mathop {\max \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - 4\(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - {{16} \over 3};\,\,\mathop {\max \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - 4\)

c) D = \left( {0; + \infty } \right);f\(D = \left( {0; + \infty } \right);f'\left( x \right) = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}}với mọi x \ne 0,f'\left( x \right) = 0 \Leftrightarrow x = \pm 1\)

x=1\in \left\{ {0; + \infty } \right.)x=-1\not\in \left\{ {0; + \infty } \right.)\(x=1\in \left\{ {0; + \infty } \right.)x=-1\not\in \left\{ {0; + \infty } \right.)\)\)

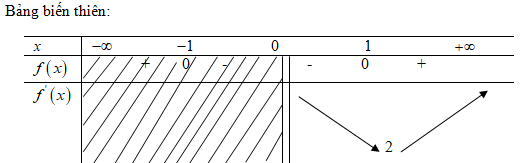
Giải bài tập Toán 12 Nâng cao bài 17 câu c

\mathop {\min \,\,f\left( x \right) = f\left( 1 \right)}\limits_{x \in \left( {0; + \infty } \right)} = 2\(\mathop {\min \,\,f\left( x \right) = f\left( 1 \right)}\limits_{x \in \left( {0; + \infty } \right)} = 2\)

Hàm số không đạt giá trị lớn nhất trên khoảng \left( {0; + \infty } \right)\(\left( {0; + \infty } \right)\)

d) D = \left[ {2;4} \right];f\(D = \left[ {2;4} \right];f'\left( x \right) = - 2x + 2;f'\left( x \right) = 0 \Leftrightarrow x = 1 \notin \left[ {2;4} \right]\)

Ta có: f\left( 2 \right) = 4;f\left( 4 \right) = - 4\(f\left( 2 \right) = 4;f\left( 4 \right) = - 4\)

Vậy\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = - 4;\,\mathop {\max f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = 4\(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = - 4;\,\mathop {\max f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = 4\)

e)

D = \left[ {0;1} \right];f\(D = \left[ {0;1} \right];f'\left( x \right) = {{2{x^2} + 8x + 6} \over {{{\left( {x + 2} \right)}^2}}};f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \notin \left[ {0;1} \right] \hfill \cr x = - 3 \notin \left[ {0;1} \right] \hfill \cr} \right.\)

Ta có: f\left( 0 \right) = 2;f\left( 1 \right) = {{11} \over 3}\(f\left( 0 \right) = 2;f\left( 1 \right) = {{11} \over 3}\)

Vậy\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = 2;\mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = {{11} \over 3}\(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = 2;\mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = {{11} \over 3}\)

f) D = \left( {0;2} \right];f\(f'\left( x \right) = 1 + {x \over {\sqrt {{x^2} - 1} }} = {{\sqrt {{x^2} - 1} + x} \over {\sqrt {{x^2} - 1} }}\)

f\(G'\left( x \right) = 1,5x - 0,075{x^2};G'\left( x \right) = 0 \Leftrightarrow x = 0 hoặc x = 20\)

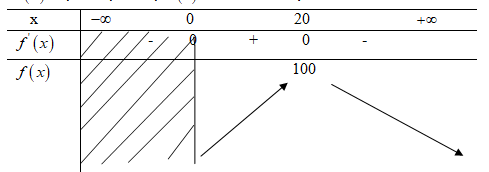
giải bài tập Toán Nâng cao 12 bài 23

\eqalign{ & \mathop {\max G\left( x \right)}\limits_{x > 0} = G\left( {20} \right) = 100 \cr & \cr}\(\eqalign{ & \mathop {\max G\left( x \right)}\limits_{x > 0} = G\left( {20} \right) = 100 \cr & \cr}\)

Liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là 20 mg. Khi đó, độ giảm huyết áp là 100

Bài 24 trang 23 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3

Cho parabol P y = x^2\(y = x^2\) và điểm A (-3;0)\(A (-3;0)\) Xác định điểm M thuộc parabol P sao cho khoảng cách AM là ngắn nhất và tìm khoảng cách ngắn nhất đó.

Giải

Gọi M\left( {x;{x^2}} \right)\(M\left( {x;{x^2}} \right)\)

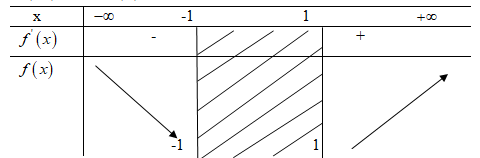
Ta có: A{M^2} = {(x + 3)^2} + {x^4} = {x^4} + {x^2} + 6x + 9\(A{M^2} = {(x + 3)^2} + {x^4} = {x^4} + {x^2} + 6x + 9\)

AM đạt giá trị nhỏ nhất khi và chỉ khif(x) = {x^4} + {x^2} + 6x + 9\(f(x) = {x^4} + {x^2} + 6x + 9\)đạt giá trị nhỏ nhất

Ta có: 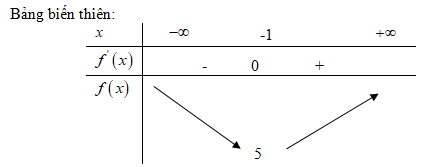f\(E'\left( v \right) = 300c.{{3{v^2}\left( {v - 6} \right) - {v^3}} \over {{{\left( {v - 6} \right)}^2}}} = 300c.{{2{v^3} - 18v} \over {{{\left( {v - 6} \right)}^2}}} = 600c.{{{v^2}\left( {v - 9} \right)} \over {{{\left( {v - 6} \right)}^2}}}\)

Năng lượng cực tiểu khi: E\(E'\left( v \right) = 0 \Leftrightarrow v = 9( vì v>6)E\left( 9 \right) = 72900c\)

Bảng biến thiên:

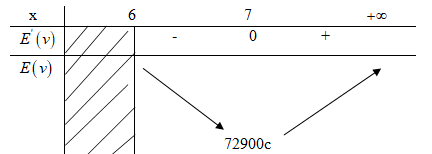
Giải bài tập Toán 12 Nâng cao bài 25

Để ít tiêu hao năng lượng nhất, cá phải bơi với vận tốc ( khi nước đứng yên) là 9 km/h

Bài 26 trang 23 sgk Toán 12 Nâng cao Đại số và Giải tích bài 3

Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là

f\left( t \right) = 45{t^2} - {t^3},t = 0,1,2,...,25\(f\left( t \right) = 45{t^2} - {t^3},t = 0,1,2,...,25\)

Nếu coi f là hàm số xác định trên đoạn

Từ khóa » Gtln Gtnn Của Hàm Số 12