Giải Bài Tập Toán 12 Nâng Cao Chương 1 Bài 8: Một Số ...

Giải bài tập Toán 12 Nâng cao Chương 1 bài 8: Một số bài toán thường gặp về đồ thị Giải sgk Toán 12 Nâng cao trang 55, 56, 57, 58 Bài trước Tải về Bài sau Lớp: Lớp 12 Môn: Toán Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Giải bài tập sgk Toán 12 Nâng cao bài 8 Đại số và Giải tích là tài liệu hướng dẫn các em giải các bài tập trong sgk Toán 12 Nâng cao. Tài liệu sẽ giúp các em làm các dạng bài toán thường gặp về đồ thị.

Giải bài tập SGK Toán 12 Nâng cao bài 8

• Bài 57 trang 55 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 58 trang 56 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 59 trang 56 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 60 trang 56 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 61 trang 56 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 62 trang 57 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 63 trang 57 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 64 trang 57 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 65 trang 58 sgk Toán 12 Nâng cao Đại số và Giải tích
• Bài 66 trang 58 sgk Toán 12 Nâng cao Đại số và Giải tích

Bài 57 trang 55 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: \(f\left( x \right) = 2{x^3} + 3{x^2} + 1\)

b) Tìm các giao điểm của đường cong (C) và parabol: \((P):\,\,\,g\left( x \right) = 2{x^2} + 1\)

c) Viết phương trình các tiếp tuyến của (C) và (P) tại mỗi giao điểm của chúng.

d) Xác định các khoảng trên đó (C) nằm phía trên hoặc phía dưới (C).

Giải

a) Tập xác định: \(D=\mathbb R\)

\(f'(x)=6x^2+6xf'(x)=0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = - 1 \hfill \cr} \right.\)

Bảng biến thiên:

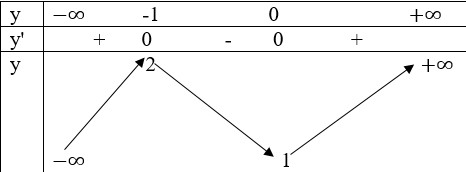
- Hàm số đồng biến trên\(( - \infty ;-1) và (0; + \infty )\)

- Hàm số nghịch biến trên (-1;0)

- Hàm số đạt cực tại \(x=-1;y_{CĐ}=2\)

- Hàm số đạt cực tiểu tại \(x=0;y_{CT}=1\)

\(\mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty\)

Đồ thị giao trục Oy tại điểm (0;1)

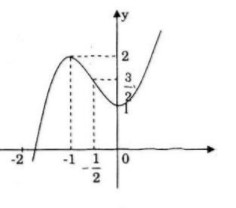
b) Hoành độ giao điểm của đường cong (C) và paraobol (P) là nghiệm của phương trình:

\(\eqalign{ & \,\,\,\,2{x^3} + 3{x^2} + 1 = 2{x^2} + 1 \Leftrightarrow 2{x^3} + {x^2} = 0 \cr & \Leftrightarrow {x^2}\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = - {1 \over 2} \hfill \cr} \right. \cr}\)

Với x = 0 ta có y = 1; với\(x = - {1 \over 2}\) ta có \(y = {3 \over 2}\)

Ta có giao điểm A(0;1) và \(B\left( { - {1 \over 2};{3 \over 2}} \right)\)

c\(f'\left( { - {1 \over 2}} \right) = - {3 \over 2}\). Phương trình tiếp tuyến của (C) tại điểm B là:

\(y'\left( 0 \right) = {3 \over 2}\) Phương trình tiếp tuyến chung của hai đường cong tại điểm gốc là \(y = {3 \over 2}x.\)

Bài 61 trang 56 sgk Toán 12 Nâng cao Đại số và Giải tích

Một viên đạn được bắn ra với vận tốc ban đầu \({v_o} > 0\) từ một nòng súng đặt ở gốc tọa độ O, nghiêng một góc \(\alpha\) với mặt đất (nòng súng nằm trong mặt phẳng thẳng đứng (Oxy) và tạo với trục hoành Ox góc\(\alpha\)). Biết quỹ đạo chuyển động của viên đạn là parabol\(\left( {{\gamma _\alpha }} \right):y = - {g \over {2v_o^2}}\left( {1 + {{\tan }^2}\alpha } \right){x^2} + x\tan \alpha\) , g là gia tốc trọng trường

Chứng minh rằng với mọi \(\alpha \in \left( {0;{\pi \over 2}} \right)\),\(\,\left( {{\gamma _\alpha }} \right)\)luôn tiếp xúc với parabol (P) có phương trình là: \(y = - {g \over {2v_o^2}}{x^2} + {{v_o^2} \over {2g}}\)và tìm tọa độ tiếp điểm (P) được gọi là parabol an toàn

Giải

Hoành độ tiếp điểm của hai parabol là nghiệm của hệ phương trình:

\(\left\{ \matrix{ - {g \over {2v_o^2}}\left( {1 + {{\tan }^2}\alpha } \right){x^2} + x\tan \alpha = - {g \over {2v_o^2}}{x^2} + {{v_o^2} \over {2g}} \hfill \cr - {g \over {v_o^2}}\left( {1 + {{\tan }^2}\alpha } \right)x + \tan \alpha = - {g \over {v_o^2}}x \hfill \cr} \right.\)

Nghiệm của phương trình thứ hai của hệ là \(x = {{v_o^2} \over {g\tan \alpha }}\)

Ta có\(x = {{v_o^2} \over {g\tan \alpha }}\)cũng là nghiệm của phương trình thứ nhất của hệ. Vậy với mọi \(\alpha \in \left( {0;{\pi \over 2}} \right)\)hai parabol luôn tiếp xúc với nhau. Hoành độ tiếp điểm là \(x = {{v_o^2} \over {g\tan \alpha }}\) . Tung độ của tiếp điểm là

\(y = - {g \over {2v_o^2}}{\left( {{{v_o^2} \over {g\tan \alpha }}} \right)^2} + {{v_o^2} \over {2g}} = {{v_o^2} \over {2g}}\left( {1 - {1 \over {{{\tan }^2}\alpha }}} \right)\)

Điểm \(\left( {{{v_o^2} \over {g\tan \alpha }};{{v_o^2} \over {2g}}\left( {1 - {{\cot }^2}\alpha } \right)} \right)\)là tiếp điểm của hai parabol với mọi \(\alpha \in \left( {0;{\pi \over 2}} \right)\)

Bài 62 trang 57 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số: \(y = {{x - 1} \over {x + 1}}\)

b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó.

Giải

Tập xác định:

\(\eqalign{ & D = R\backslash \left\{ { - 1} \right\} \cr & \cr}\)

Sự biến thiên:

\(y' = {2 \over {{{(x + 1)}^2}}} > 0\,\forall x \in D\)

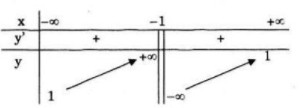
Hàm số đồng biến trên khoảng\(( - \infty ; - 1) và ( - 1; + \infty )\)

Giới hạn:

\(\mathop {\lim y}\limits_{x \to - {1^ - }} = + \infty ;\,\mathop {\lim y}\limits_{x \to - {1^ + }} = - \infty\)

Tiệm cận đứng: x=-1

\(\mathop {\lim y}\limits_{x \to \pm \infty } = 1\)

Tiệm cận ngang: y=1

Bảng biến thiên:

Đồ thị giao Ox tại điểm (1;0)

Đồ thị giao Oy tại điểm (0;-1)

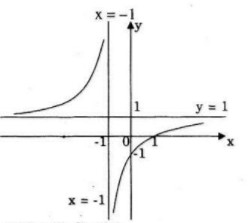
b) Giao điểm của hai tiệm cận của đường cong là I(-1;1)

Công thức đổi trục tịnh tiến theo vecto \(\overrightarrow {OI}\) là

\(\left\{ \matrix{ x = X - 1 \hfill \cr y = Y + 1 \hfill \cr} \right.\)

Phương trình đường cong trong hệ tọa độ IXY là:

\(Y + 1 = {{X - 1 - 1} \over {X - 1 + 1}} \Leftrightarrow Y + 1 = {{X - 2} \over X} \Leftrightarrow Y = - {2 \over X}\)

Đây là hàm số lẻ nên đồ thị nhận gốc I làm tâm đối xứng.

Bài 63 trang 57 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số: \(y = {{x + 2} \over {2x + 1}}\)

b) Chứng minh rằng đường thẳng \(y = mx + m - 1\) luôn đi qua một điểm cố định của đường cong (H) khi m biến thiên.

c) Tìm các giá trị của m sao cho đường thẳng đã cho cắt đường cong (H) tại hai điểm thuộc cùng một nhánh của (H).

Giải

a) Tập xác định:\(D =\mathbb R\backslash \left\{ { - {1 \over 2}} \right\}\)

+) Sự biến thiên:

\(y' = {{ - 3} \over {{{(2x + 1)}^2}}} < 0\,\forall x \in D\)

Hàm số nghịch biến trên khoảng\(\left( { - \infty ; - {1 \over 2}} \right)\) và \(\left( { - {1 \over 2}; + \infty } \right)\)

Giới hạn:

\(\mathop {\lim y}\limits_{x \to - {{{1 \over 2}}^ - }} = - \infty ;\,\mathop {\lim y}\limits_{x \to - {{{1 \over 2}}^ + }} = + \infty\)

Hầm số không có cực trị.

Tiệm cận đứng:\(x={ - {1 \over 2}}\)

\(\mathop {\lim y}\limits_{x \to \pm \infty } = {1 \over 2}\)

Tiệm cận ngang\(y={1 \over 2}\)

Bảng biến thiên:

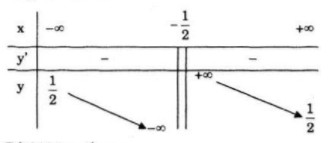
Đồ thị giao Ox tại điểm (-2;0)

Đồ thị giao Oy tại điểm (0;2)

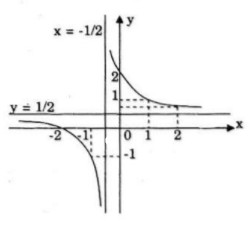
b) Ta có \(y = mx + m - 1 \Leftrightarrow y + 1 = m\left( {x + 1} \right)\)

Tọa độ điểm cố định A của đường thẳng là nghiệm của hệ:

\(\left\{ \matrix{ x + 1 = 0 \hfill \cr y + 1 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 1 \hfill \cr y = - 1 \hfill \cr} \right.\)

Vậy A(-1;1)

Tọa độ A thỏa mãn phương trình \(y = {{x + 2} \over {2x + 1}}\)nên A thuộc đường cong (H).

c) Hoành độ giao điểm của đường thẳng đã cho và đường cong (H) là nghiệm của phương trình:

\(\eqalign{ & \,\,\,m\left( {x + 1} \right) - 1 = {{x + 2} \over {2x + 1}} \Leftrightarrow \left( {2x + 1} \right)\left[ {m\left( {x + 1} \right) - 1} \right] = x + 2 \cr & \Leftrightarrow m\left( {x + 1} \right)\left( {2x + 1} \right) - \left( {2x + 1} \right) = x + 2 \cr & \Leftrightarrow \left( {x + 1} \right)\left( {2mx + m - 3} \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr f\left( x \right) = 2mx + m - 3 = 0\,\,\,\left( 1 \right) \hfill \cr} \right. \cr}\)

Hai nhánh của (H) nằm về hai bên của tiệm cận đứng \(x = - {1 \over 2}\)

Điểm A(-1;1) thuộc nhánh trái của (H) vì \({x_A} = - 1 < - {1 \over 2}\)

Đường thẳng cắt (H) tại hai điểm thuộc cùng một nhánh khi và chỉ khi (1) có nghiệm \(x < - {1 \over 2} và(x \ne - 1\)\(tức \left\{ \matrix{ x \ne 0 \hfill \cr x = {{ - m + 3} \over 2} < - {1 \over 2} \hfill \cr f\left( { - 1} \right) \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ m \ne 0 \hfill \cr {3 \over {2m}} < 0 \hfill \cr - m - 3 \ne 0 \hfill \cr} \right. \Leftrightarrow m < - 3\,\, \text{hoặc}\, - 3 < m < 0.\)

Bài 64 trang 57 sgk Toán 12 Nâng cao Đại số và Giải tích

.Cho hàm số \(y = {{a{x^2} - bx} \over {x - 1}}\)

a) Tìm a và b biết rằng đồ thị (C) của hàm số đã cho đi qua điểm \(A\left( { - 1;{5 \over 2}} \right)\) và tiếp tuyến của (C) tại điểm O(0;0) có hệ số bằng -3.

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị của a và b đã tìm được.

Giải

a) Ta có: \({M_o} \in \left( C \right) y' = {{\left( {12ax - b} \right)\left( {x - 1} \right) - \left( {a{x^2} - bx} \right)} \over {{{\left( {x - 1} \right)}^2}}}\)

Đồ thị (C) đi qua \(A\left( { - 1;{5 \over 2}} \right) \Leftrightarrow y\left( { - 1} \right) = {5 \over 2} \Leftrightarrow {{a + b} \over { - 2}} = {5 \over 2} \Leftrightarrow a + b = - 5\,\,\,\left( 1 \right)\)

Tiếp tuyến của (C) tại O(0;0) có hệ số góc bằng -3 khi và chỉ khi \(y’(0) = -3 \Leftrightarrow b = - 3\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra a = -2; b = - 3.

b) Với a = -2; b = - 3 ta có:\(y = {{ - 2{x^3} + 3x} \over {x - 1}}\)

Tập xác định: \(D = \mathbb R\backslash \left\{ 1 \right\}\)

\(y' = {{ - 2{x^2} + 4x - 3} \over {{{(x - 1)}^2}}} < 0\,\forall x \in D\)

Hàm số nghịch biến trên khoảng:\(( - \infty ;1) và (1; + \infty )\)

Hàm số không có cực trị

Giới hạn:

\(\mathop {\lim y}\limits_{x \to {1^ - }} = - \infty ;\,\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty\)

Tiệm cận đứng là: x=1

\(\eqalign{ & a = \mathop {\lim }\limits_{x \to \infty } {y \over x} = \mathop {\lim }\limits_{x \to \infty } {{ - 2{x^2} + 3x} \over {{x^2} - x}} = - 2 \cr & b = \mathop {\lim }\limits_{x \to \infty } (y + 2x) = \mathop {\lim }\limits_{x \to \infty } \left( {{{ - 2{x^2} + 3x} \over {x - 1}} + 2x} \right) = 1 \cr}\)

Tiệm cận xiên là: y=-2x+1

Bảng biến thiên:

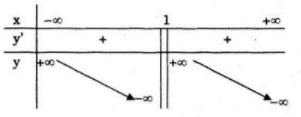
Đồ thị giao Oy tại điểm (0;0) và \(\left( {{3 \over 2};0} \right)\)

Bài 65 trang 58 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {{2{x^2} - x + 1} \over {x - 1}}\)

b) Với các giá trị nào t=của m đường thẳng y = m – x cắt đồ thị hàm số đã cho tại hao điểm phân biệt?

c) Gọi A và B là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng AB khi m biến thiên.

Giải

a) Tập xác định: \(D = \mathbb R\backslash \left\{ 1 \right\}\)

Sự biến thiên:

\(\eqalign{ & y' = {{2{x^2} - 4x} \over {{{(x - 1)}^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 2 \hfill \cr} \right. \cr}\)

Hàm số đồng biến trên khoảng\(( - \infty ;0) và((2; + \infty )\)

Hàm số nghịch biến trên khoảng (0;1) và (1;2)

Cực trị

Hàm số đạt cực đại tại x=0, \(y_{CĐ}=1\)

Hàm số đạt cực tiểu tại x=2, \(y_{CT}=7\)

Giới hạn:

\(\mathop {\lim y}\limits_{x \to {1^ - }} = - \infty ;\,\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty\)

Tiệm cận đứng là: x=1

\(\eqalign{ & a = \mathop {\lim }\limits_{x \to \infty } {y \over x} = \mathop {\lim }\limits_{x \to \infty } {{2{x^2} - x + 1} \over {{x^2} - x}} = 2 \cr & b = \mathop {\lim }\limits_{x \to \infty } (y - 2x) = \mathop {\lim }\limits_{x \to \infty } \left( {{{2{x^2} - x + 1} \over {x - 1}} - 2x} \right) = 1 \cr}\)

Tiệm cận xiên là: y=2x+1

Bảng biến thiên:

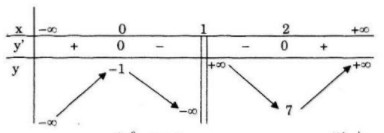
Đồ thị cắt (Oy) tại điểm ((0;-1)

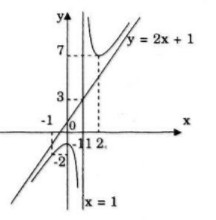
b) Hoành độ giao điểm của đường thẳng và đường cong đã cho là nghiệm của phương trình

\(\eqalign{ & {{2{x^2} - x + 1} \over {x - 1}} = m - 1 \Leftrightarrow 2{x^2} - x + 1 = \left( {x - 1} \right)\left( {m - x} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 3{x^2} - \left( {m + 2} \right)x + m + 1 = 0\,\,\left( 1 \right) \cr}\)

(vì x =1) không là nghiệm của hai phương trình)

Đường thẳng cắt đường cong tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt, tức là

\(\eqalign{ & \Delta = {\left( {m + 2} \right)^2} - 12\left( {m + 1} \right) > 0 \Leftrightarrow {m^2} - 8m - 8 > 0 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow m < 4 - 2\sqrt 6 \,\,\text{hoặc}\,\,m > 4 + 2\sqrt {6\,\,} \,\,\,\,\left( 2 \right) \cr}\)

c) Hoành độ giao điểm A, B là các nghiệm của (1)

Hoành độ trung điểm M của AB là:\({x_M} = {1 \over 2}\left( {{x_A} + {x_B}} \right) = {{m + 2} \over 6}\)

Vì M nằm trên đường thẳng y = m – x nên\({y_M} = m - {x_M} = m - {{m + 2} \over 6} = {{5m - 2} \over 6}\)

Khử m từ hệ

\(\left\{ \matrix{ {x_M} = {{m + 2} \over 6} \hfill \cr {y_M} = {{5m - 2} \over 6} \hfill \cr} \right.\) ta được:\(5{x_M} - {y_M} = 2 \Leftrightarrow {y_M} = 5{x_M} - 2\)

Vậy M nằm trên đường thẳng y = 5x -2

Vì m chỉ lấy giá trị thỏa mãn (2) nên:

\(m < 4 - 2\sqrt 6 \Rightarrow m = 6{x_M} - 2 < 4 - 2\sqrt 6 \Rightarrow {x_M} < 1 - {{\sqrt 6 } \over 3}\)

\(m > 4 + 2\sqrt 6 \Rightarrow m = 6{x_M} - 2 > 4 + 2\sqrt 6 \Rightarrow {x_M} > 1 + {{\sqrt 6 } \over 3}\)

Vậy tập hợp các trung điểm M của đoạn AB là phần của đường thẳng y = 5x -2 với \({x_M} < 1 - {{\sqrt 6 } \over 3}\) hoặc\({x_M} > 1 + {{\sqrt 6 } \over 3}\)

Bài 66 trang 58 sgk Toán 12 Nâng cao Đại số và Giải tích

Tìm các hệ số a, b sao cho parabol \(y = 2{x^2} + ax + b\) tiếp xúc với hypebol \(y = {1 \over x}\)tại điểm \(M\left( {{1 \over 2};2} \right)\)

Giải

Giả sử \(f\left( x \right) = 2{x^2} + ax + b;\,g\left( x \right) = {1 \over x}\)

Parabol tiếp xúc với hypebol tại \(M\left( {{1 \over 2};2} \right)\) khi và chỉ khi