Giải Bài Tập Toán 12 Nâng Cao Đại Số Và Giải Tích Bài 1
Có thể bạn quan tâm
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ ZaloGiải bài tập Toán 12 Nâng cao Đại số và Giải tích bài 1 tích hợp và hướng dẫn giải các dạng bài tập về phần đại số của môn Toán 12 nâng cao.Tài liệu được trình bày một cách cụ thể, rõ ràng để các em nắm bắt kiến thức.
Giải bài tập sgk Toán 12 Nâng cao bài 1
- Bài 1 trang 7 SGK Đại số và Giải tích 12 Nâng cao
- Bài 2 trang 7 SGK Đại số và Giải tích 12 Nâng cao
- Bài 3 trang 7 SGK Đại số và Giải tích 12 Nâng cao
- Bài 4 trang 7 SGK Đại số và Giải tích 12 Nâng cao
- Bài 5 trang 8 SGK Đại số và Giải tích 12 Nâng cao
- Bài 6 trang 8 SGK Đại số và Giải tích 12 Nâng cao
- Bài 7 trang 8 SGK Đại số và Giải tích 12 Nâng cao
- Bài 8 trang 8 SGK Đại số và Giải tích 12 Nâng cao.
- Bài 9 trang 9 SGK Đại số và Giải tích 12 Nâng cao.
- Bài 10 trang 9 SGK Đại số và Giải tích 12 Nâng cao.
Bài 1 trang 7 SGK Đại số và Giải tích 12 Nâng cao
Xét chiều biến thiên của các hàm số sau:
![]() \(a) y = 2{x^3} + 3{x^2} + 1\)
\(a) y = 2{x^3} + 3{x^2} + 1\)
![]() \(b) \,y = {x^3} - 2{x^2} + x + 1\)
\(b) \,y = {x^3} - 2{x^2} + x + 1\)
![]() \(c) y = x + {3 \over x}\)
\(c) y = x + {3 \over x}\)
d) ![]() \(y = x - {2 \over x}\)
\(y = x - {2 \over x}\)
e) ![]() \(y = {x^4} - 2{x^2} - 5\)
\(y = {x^4} - 2{x^2} - 5\)
![]() \(f) y = \sqrt {4 - {x^2}}\)
\(f) y = \sqrt {4 - {x^2}}\)
Giải
a) Tập xác định:![]() \(D =\mathbb R\)
\(D =\mathbb R\)
 \(\eqalign{ & y' = 6{x^2} + 6x \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0\,\,\left( {y = 1} \right) \hfill \cr x = - 1\,\,\left( {y = 2} \right) \hfill \cr} \right. \cr}\)
\(\eqalign{ & y' = 6{x^2} + 6x \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0\,\,\left( {y = 1} \right) \hfill \cr x = - 1\,\,\left( {y = 2} \right) \hfill \cr} \right. \cr}\)
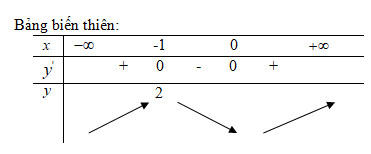
Hàm số đồng biến trên mỗi khoảng ![]() \(\left( { - \infty ; - 1} \right)\)và
\(\left( { - \infty ; - 1} \right)\)và ![]() \(\left( {0; + \infty } \right)\)nghịch biến trên khoảng
\(\left( {0; + \infty } \right)\)nghịch biến trên khoảng![]() \(\left( { - 1;0} \right)\)
\(\left( { - 1;0} \right)\)
b) Tập xác định: ![]() \(D =\mathbb R\)
\(D =\mathbb R\)
 \(\eqalign{ & y' = 3{x^2} - 4x + 1 \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 1\,\,\left( {y = 1} \right) \hfill \cr x = {1 \over 3}\,\,\left( {y = {{31} \over {27}}} \right) \hfill \cr} \right. \cr}\)
\(\eqalign{ & y' = 3{x^2} - 4x + 1 \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 1\,\,\left( {y = 1} \right) \hfill \cr x = {1 \over 3}\,\,\left( {y = {{31} \over {27}}} \right) \hfill \cr} \right. \cr}\)
Bảng biến thiên
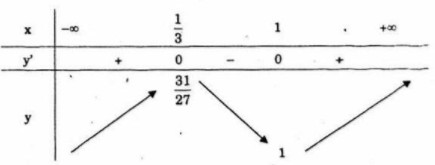
Hàm số đồng biến trên mỗi khoảng ![]() \(\left( { - \infty ;{1 \over 3}} \right)\) và
\(\left( { - \infty ;{1 \over 3}} \right)\) và ![]() \(\,\left( {1; + \infty } \right)\), nghịch biến trên khoảng
\(\,\left( {1; + \infty } \right)\), nghịch biến trên khoảng ![]() \(\,\left( {{1 \over 3};1} \right)\).
\(\,\left( {{1 \over 3};1} \right)\).
c) Tập xác định: ![]() \(D =\mathbb R\backslash \left\{ 0 \right\}\)
\(D =\mathbb R\backslash \left\{ 0 \right\}\)
 \(\eqalign{ & y' = 1 - {3 \over {{x^2}}} = {{{x^2} - 3} \over {{x^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = \sqrt 3 \,\,\left( {y = 2\sqrt 3 } \right) \hfill \cr x = - \sqrt 3 \,\,\left( {y = - 2\sqrt 3 } \right) \hfill \cr} \right. \cr}\)
\(\eqalign{ & y' = 1 - {3 \over {{x^2}}} = {{{x^2} - 3} \over {{x^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = \sqrt 3 \,\,\left( {y = 2\sqrt 3 } \right) \hfill \cr x = - \sqrt 3 \,\,\left( {y = - 2\sqrt 3 } \right) \hfill \cr} \right. \cr}\)
Bảng biến thiên
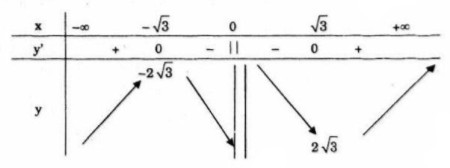
Hàm số đồng biến trên mỗi khoảng ![]() \(\left( { - \infty ; - \sqrt 3 } \right)\) và
\(\left( { - \infty ; - \sqrt 3 } \right)\) và ![]() \(\,\left( {\sqrt 3 ; + \infty } \right)\), nghịch biến trên khoảng
\(\,\left( {\sqrt 3 ; + \infty } \right)\), nghịch biến trên khoảng ![]() \(\left( { - \sqrt 3 ;0} \right)\) và
\(\left( { - \sqrt 3 ;0} \right)\) và ![]() \(\,\left( {0;\sqrt 3 } \right)\)
\(\,\left( {0;\sqrt 3 } \right)\)
d) Tập xác định: ![]() \(D = \mathbb R\backslash \left\{ 0 \right\}\)
\(D = \mathbb R\backslash \left\{ 0 \right\}\)
Hàm số đồng biến trên mỗi khoảng ![]() \(\,\,\left( { - \infty ;0} \right)\) và
\(\,\,\left( { - \infty ;0} \right)\) và ![]() \(\left( {0; + \infty } \right)\)
\(\left( {0; + \infty } \right)\)
e) Tập xác định: ![]() \(D= \mathbb R\)
\(D= \mathbb R\)
 \(y' = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right)\);
\(y' = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right)\); \(y' = 0\)
\(y' = 0\)
![]() \(\Leftrightarrow \,\)
\(\Leftrightarrow \,\)![]() \(\left[ \matrix{ x = 0\,\,\,\,\left( {y = - 5} \right) \hfill \cr x = \pm 1\,\,\,\,\left( {y = - 6} \right) \hfill \cr} \right.\)
\(\left[ \matrix{ x = 0\,\,\,\,\left( {y = - 5} \right) \hfill \cr x = \pm 1\,\,\,\,\left( {y = - 6} \right) \hfill \cr} \right.\)
Bảng biến thiên
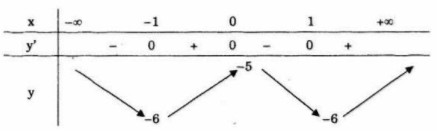
Hàm số đồng biến trên mỗi khoảng![]() \(\,\left( { - \infty ; - 1} \right)\)và
\(\,\left( { - \infty ; - 1} \right)\)và![]() \(\left( {0;1} \right)\), đồng biến trên mỗi khoảng
\(\left( {0;1} \right)\), đồng biến trên mỗi khoảng ![]() \(\left( { - 1;0} \right)\) và
\(\left( { - 1;0} \right)\) và ![]() \(\left( {1; + \infty } \right)\)
\(\left( {1; + \infty } \right)\)
f) Hàm số xác định khi và chỉ khi ![]() \(4 - {x^2} \ge 0\)
\(4 - {x^2} \ge 0\) ![]() \(\Leftrightarrow\)
\(\Leftrightarrow\) ![]() \(- 2 \le x \le 2\)
\(- 2 \le x \le 2\)
Tập xác định: ![]() \(D = \left[ { - 2;2} \right]\)
\(D = \left[ { - 2;2} \right]\)
 \(y' = {{ - 2x} \over {2\sqrt {4 - {x^2}} }} = {{ - x} \over {\sqrt {4 - {x^2}} }};y' = 0 \Leftrightarrow x = 0\,\,\,\left( {y = 2} \right)\)
\(y' = {{ - 2x} \over {2\sqrt {4 - {x^2}} }} = {{ - x} \over {\sqrt {4 - {x^2}} }};y' = 0 \Leftrightarrow x = 0\,\,\,\left( {y = 2} \right)\)
Bảng biến thiên![]() \(\left( {1; + \infty } \right)\)
\(\left( {1; + \infty } \right)\)
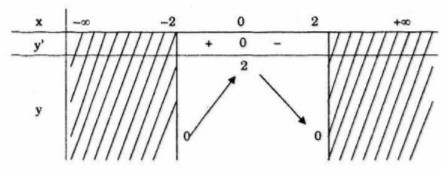
Hàm số đồng biến trên khoảng ![]() \(\left( { - 2;0} \right)\)và nghịch biến trên khoảng
\(\left( { - 2;0} \right)\)và nghịch biến trên khoảng ![]() \(\left( {0;2} \right)\) .
\(\left( {0;2} \right)\) .
Bài 2 trang 7 SGK Đại số và Giải tích 12 Nâng cao
Chứng minh rằng:
a) Hàm số ![]() \(y = {{x - 2} \over {x + 2}}\) đồng biến trên mỗi khoảng xác định của nó.
\(y = {{x - 2} \over {x + 2}}\) đồng biến trên mỗi khoảng xác định của nó.
b)Hàm số ![]() \(y = {{ - {x^2} - 2x + 3} \over {x + 1}}\) nghịch biến trên mỗi khoảng xác định của nó.
\(y = {{ - {x^2} - 2x + 3} \over {x + 1}}\) nghịch biến trên mỗi khoảng xác định của nó.
Giải
a) Tập xác định:
 \(D =\mathbb R\backslash \left\{ { - 2} \right\}y' = {{\left| \matrix{ 1\,\,\,\, - 2 \hfill \cr 1\,\,\,\,\,\,\,\,2 \hfill \cr} \right|} \over {{{\left( {x + 2} \right)}^2}}} = {4 \over {{{\left( {x + 2} \right)}^2}}} > 0 vớimọi x \ne - 2\)
\(D =\mathbb R\backslash \left\{ { - 2} \right\}y' = {{\left| \matrix{ 1\,\,\,\, - 2 \hfill \cr 1\,\,\,\,\,\,\,\,2 \hfill \cr} \right|} \over {{{\left( {x + 2} \right)}^2}}} = {4 \over {{{\left( {x + 2} \right)}^2}}} > 0 vớimọi x \ne - 2\)
Hàm số đồng biến trên mỗi khoảng![]() \(\left( { - \infty ; - 2} \right)\) và
\(\left( { - \infty ; - 2} \right)\) và ![]() \(\left( { - 2; + \infty } \right)\)
\(\left( { - 2; + \infty } \right)\)
b)Tập xác định:
 \(D =\mathbb R\backslash \left\{ { - 1} \right\}(y' = {{\left( { - 2x - 2} \right)\left( {x + 1} \right) - \left( { - {x^2} - 2x + 3} \right)} \over {{{\left( {x + 1} \right)}^2}}} = {{ - {x^2} - 2x - 5} \over {{{\left( {x + 1} \right)}^2}}} < 0 với mọi x \ne - 1\)
\(D =\mathbb R\backslash \left\{ { - 1} \right\}(y' = {{\left( { - 2x - 2} \right)\left( {x + 1} \right) - \left( { - {x^2} - 2x + 3} \right)} \over {{{\left( {x + 1} \right)}^2}}} = {{ - {x^2} - 2x - 5} \over {{{\left( {x + 1} \right)}^2}}} < 0 với mọi x \ne - 1\)
Hàm số nghịch biến trên mỗi khoảng ![]() \(\left( { - \infty ; - 1} \right)\)và
\(\left( { - \infty ; - 1} \right)\)và ![]() \(\left( { - 1; + \infty } \right)\)
\(\left( { - 1; + \infty } \right)\)
Bài 3 trang 8 SGK Đại số và Giải tích 12 Nâng cao
Chứng minh rằng các hàm số sau đây đồng biến trên ![]() \(\mathbb R\)
\(\mathbb R\)
a) ![]() \(f\left( x \right)\)=
\(f\left( x \right)\)= ![]() \({x^3} - 6{x^2} + 17x + 4\)
\({x^3} - 6{x^2} + 17x + 4\)
b)![]() \(f\left( x \right)\)=
\(f\left( x \right)\)= ![]() \({x^3} + x - \cos x - 4\)
\({x^3} + x - \cos x - 4\)
Giải
a) Tập xác định:![]() \(D =\mathbb R\)
\(D =\mathbb R\)
![]() \(a < 0 thì y' < 0 với mọi x \in {\mathbb R}\), khi đó hàm số nghịch biến trên
\(a < 0 thì y' < 0 với mọi x \in {\mathbb R}\), khi đó hàm số nghịch biến trên![]() \(\mathbb R\)
\(\mathbb R\)
• Nếu  \(a = 0 thì y' = - 3{x^2} \le 0\)với mọi
\(a = 0 thì y' = - 3{x^2} \le 0\)với mọi ![]() \(x \in {\mathbb R}\),
\(x \in {\mathbb R}\), \(y'=0\Leftrightarrow x=0\).
\(y'=0\Leftrightarrow x=0\).
Vậy hàm số nghịch biến trên ![]() \(\mathbb R\).
\(\mathbb R\).
• Nếu  \(a > 0 thì y' = 0 \Leftrightarrow x = \pm {\sqrt {a \over 3}}\)
\(a > 0 thì y' = 0 \Leftrightarrow x = \pm {\sqrt {a \over 3}}\)
Bảng biến thiên

Trong trường hợp này, hàm số không đồng biến trên ![]() \({\mathbb R}\)
\({\mathbb R}\)
Vậy hàm số nghịch biến trên ![]() \({\mathbb R}\) khi và chỉ khi
\({\mathbb R}\) khi và chỉ khi ![]() \(a \le 0\)
\(a \le 0\)
Bài 5 trang 8 SGK Đại số và Giải tích 12 Nâng cao
Tìm các giá trị của tham số![]() \(a\) để hàm số
\(a\) để hàm số ![]() \(f\left( x \right) = {1 \over 3}{x^3} + a{x^2} + 4x + 3\)đồng biến trên
\(f\left( x \right) = {1 \over 3}{x^3} + a{x^2} + 4x + 3\)đồng biến trên ![]() \(\mathbb R\)
\(\mathbb R\)
Giải
Tập xác định![]() \(f'\left( x \right) = - 2\sin 2x - 2 \le 0\Leftrightarrow - 2\left( {\sin 2x + 1} \right) \le 0,\forall x \in \mathbb R\)
\(f'\left( x \right) = - 2\sin 2x - 2 \le 0\Leftrightarrow - 2\left( {\sin 2x + 1} \right) \le 0,\forall x \in \mathbb R\)
 \(f'\left( t \right) = {{120} \over {{{\left( {t + 5} \right)}^2}}} > 0 với mọi t>0\)
\(f'\left( t \right) = {{120} \over {{{\left( {t + 5} \right)}^2}}} > 0 với mọi t>0\)
Hàm số đồng biến trên ![]() \(\left[ {0; + \infty } \right)\)
\(\left[ {0; + \infty } \right)\)
c) Tốc độ tăng dân số vào năm ![]() \(1990\) là
\(1990\) là
Từ khóa » Giải Bài Toán Lớp 12 Nâng Cao
-
GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
Giải Bài Tập SGK Toán 12 Nâng Cao Chi Tiết, đầy đủ
-
Giải Bài Tập Toán 12 Nâng Cao, Toán 12 Nâng Cao, đầy đủ Giải Tích ...
-
Toán Nâng Cao 12 - Tìm đáp án, Giải Bài Tập, để Học Tốt
-
Giải Toán 12 SGK (Nâng Cao) - Chữa Bài Tập
-
Giải Bài Tập Giải Tích 12 Nâng Cao - Sách Toán - Học Toán
-
Bài Tập Toán Lớp 12 Nâng Cao
-
Giải Bài Tập Toán Nâng Cao Đại Số Và Giải Tích 12 Bài 2
-
Toán Lớp 12 Nâng Cao
-
Sách Giáo Khoa Giải Tích 12 Nâng Cao
-
Giải Bài Tập Nâng Cao Toán 12 - Hoc247
-
Bài 3: Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số
-
Câu 2.103 Trang 87 Sách Bài Tập Giải Tích 12 Nâng Cao
-
Sách Giải Bài Tập Giải Tích 12 Nâng Cao | Shopee Việt Nam