Giải SBT Toán 11 Bài 1: Hàm Số Lượng Giác

Giải SBT Toán 11 bài 1: Hàm số lượng giác Giải SBT Toán lớp 11 Bài trước Tải về Bài sau Lớp: Lớp 11 Môn: Toán Dạng tài liệu: Giải bài tập Loại File: PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Toán 11 - Hàm số lượng giác

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải SBT Toán 11 bài 1: Hàm số lượng giác, chắc chắn nội dung tài liệu sẽ là nguồn thông tin hữu ích để phục vụ công việc học tập của các bạn học sinh được tốt hơn.

Giải bài tập Toán 11 ôn tập chương 3: Dãy số - Cấp số cộng và cấp số nhân

Giải bài tập Toán 11 bài 4: Cấp số nhân

80 câu hỏi trắc nghiệm cấp số cộng, cấp số nhân

Hàm số lượng giác

Bài 1.1 trang 12 Sách bài tập (SBT) Đại số và giải tích 11

Tìm tập xác định của các hàm số.

a) y=cos.2x/x−1

b) y=tan.x/3

c) y=cot2x

d) y=sin.1/x2−1

Giải:

a) D=R∖{1}

b) cosx/3≠0⇔x/3≠π/2+kπ⇔x≠3π/2+k3π,k∈Z

Vậy D=R∖{3π/2+k3π,k∈Z}

c) sin2x≠0⇔2x≠kπ⇔x≠k.π/2,k∈Z

Vậy D=R∖{k.π/2,k∈Z}

d) D=R∖{−1;1}

Bài 1.2 trang 12 Sách bài tập (SBT) Đại số và giải tích 11

Tìm tập xác định của các hàm số.

a) y=\(\sqrt{\cos x+1}\)

b) y=3/sin2x−cos2x

c) y=2/cosx−cos3x

d) y=tanx+cotxy=tan⁡x+cot⁡x

Giải:

a) cosx+1≥0,∀x∈R. Vậy D = R

b) sin2x−cos2x=−cos2x≠0⇔2x≠π/2+kπ, k∈Z⇔x≠π/4+k.π/2, k∈Z

Vậy D=R∖{π/4+k.π/2,k∈Z}

c) cosx−cos3x=−2sin2xsin(−x)=4sin2xcosx

⇒cosx−cos3x≠0⇔sinx≠0 và cosx≠0

⇔x≠kπ và x≠π/2+kπ,k∈Z

Vậy D=R∖{k.π/2,k∈Z}

d) tan x và cos x có nghĩa khi sin x ≠ 0 và cos x ≠ 0

Vậy D=R∖{kπ/2,k∈Z}

Bài 1.3 trang 12 Sách bài tập (SBT) Đại số và giải tích 11

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số

a) y=3−2|sinx|

b) y=cosx+cos(x−π3)

c) y=cos2x+2cos2x

d) y=\(\sqrt{5-2\cos^2x\sin^2x}\)

Giải:

a) 0≤|sinx|≤1nn−2≤−2|sinx|≤0

Vậy giá trị lớn nhất của y = 3 - 2|sin x| là 3, đạt được khi sin x = 0; giá trị nhỏ nhất của y là 1, đạt được khi sin x = ± 1

b) cosx+cos(x−π/3)

=2cos(x−π/6)cosπ/6

=√3cos(x−π/6)

Vậy giá trị nhỏ nhất của y là -√3 đạt được chẳng hạn, tại x=7π/6; giá trị lớn nhất của y là √3, đạt được chẳng hạn tại x=π/6

c) Ta có:

cos2x+2cos2x

=1+cos2x/2+2cos2x

=1+5cos2x/2

Vì -1 ≤ cos2x ≤ 1 nên giá trị lớn nhất của y là 3, đạt được khi x = 0, giá trị nhỏ nhất của y là -2, đạt được khi x=π/2

d) 5−2cos2xsin2x=5−1/2sin22x

Vì 0≤sin22x≤1nn−1/2≤−1/2sin22x≤0

⇒3√2/2≤y≤√5

Suy ra giá trị lớn nhất của y = √5 tại x=k.π/2, giá trị nhỏ nhất là 3√2/2 tại x=π/4+k.π/2

Bài 1.4 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Với những giá trị nào của x, ta có mỗi đẳng thức sau?

a) 1/tanx=cotx

b) 1/1+tan2x=cos2x

c) 1/sin2x=1+cot2x

d) tanx+cotx=2/sin2x

Giải

a) Đẳng thức xảy ra khi các biểu thức ở hai vế có nghĩa tức là sinx ≠ 0 và cosx ≠ 0. Vậy đẳng thức xảy ra khi x≠k.π/2, k ∈ Z

b) Đẳng thức xảy ra khi cosx ≠ 0, tức là khi x≠π/2++kπ k ∈ Z

c) Đẳng thức xảy ra khi sinx ≠ 0, tức là x≠kπ, k ∈ Z

d) Đẳng thức xảy ra khi sinx ≠ 0 và cosx ≠ 0, tức là x≠k.π/2, k ∈ Z

Bài 1.5 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Xác định tính chẵn lẻ của các hàm số

a) y=cos2x/x

b) y=x−sinx

c) y=√1−cosx

d) y=1+cosxsin(3π/2−2x)

Giải

a) y=cos2x/x là hàm số lẻ

b) y=x−sinx là hàm số lẻ

c) y=√1−cosx là hàm số chẵn

d) y=1+cosxsin(3π/2−2x) là hàm số chắn

Bài 1.6 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

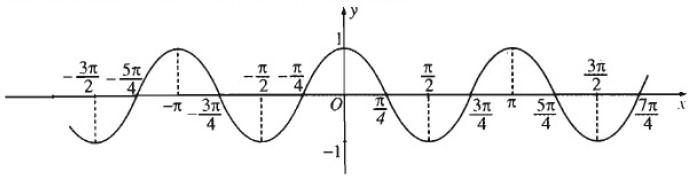
a) Chứng minh rằng cos2(x+kπ)=cos2x,k∈Z. Từ đó vẽ đồ thị hàm số y = cos 2x

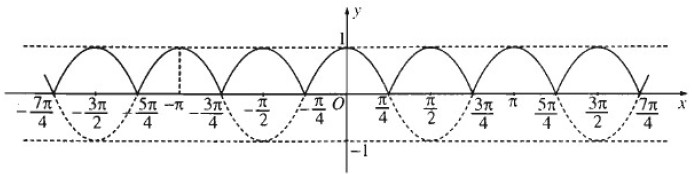
b) Từ đồ thị hàm số y = cos 2x, hãy vẽ đồ thị hàm số y = |cos 2x|

Giải:

a) cos2(x+kπ)=cos(2x+k2π)=cos2x,k∈Z. Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.

Đồ thị hàm số y = cos 2x

b) Đồ thị hàm số y = |cos 2x|

Bài 1.7 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Hãy vẽ đồ thị của các hàm số

a) y = 1 + sin x

b) y = cos x - 1

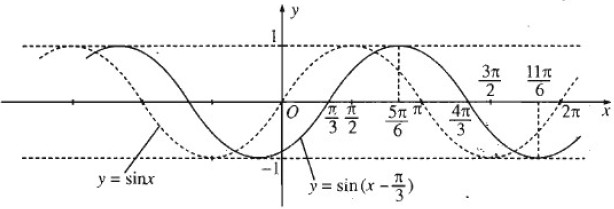
c) y=sin(x−π/3)

d) y=cos(x+π/6)

Giải:

a) Đồ thị hàm số y = 1 + sin x thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục tung lên phía trên một đơn vị.

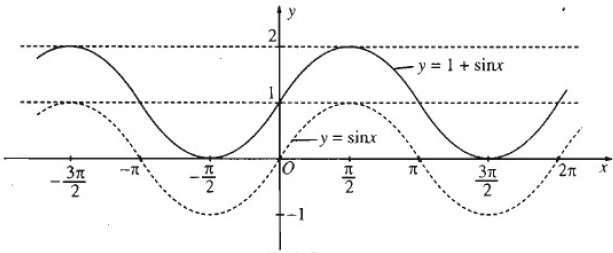
b) Đồ thị hàm số y = cos x - 1 thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục tung xuống phía dưới một đơn vị.

c) Đồ thị hàm số y=sin(x−π/3) thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng π/3.

d) Đồ thị hàm số y=cos(x+π/6) thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng π/6.

Bài 1.8 trang 13 Sách bài tập (SBT) Đại số và giải tích 11

Hãy vẽ đồ thị của các hàm số

a) y=tan(x+π/4)

b) y=cot(x−π/6)

Giải:

a) Đồ thị hàm số y=tan(x+π/4) thu được từ đồ thị hàm số y = tanx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng π/4.

b) Đồ thị hàm số y=cot(x−π/6) thu được từ đồ thị hàm số y = cotx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng π/6.

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 1: Hàm số lượng giác. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.